Essential complexity

Last updated

Essential complexity is a numerical measure defined by Thomas J. McCabe, Sr., in his highly cited, 1976 paper better known for introducing cyclomatic complexity. McCabe defined essential complexity as the cyclomatic complexity of the reduced CFG (control-flow graph) after iteratively replacing (reducing) all structured programming control structures, i.e. those having a single entry point and a single exit point (for example if-then-else and while loops) with placeholder single statements. [1] : 317  [2] : 80 

McCabe's reduction process is intended to simulate the conceptual replacement of control structures (and actual statements they contain) with subroutine calls, hence the requirement for the control structures to have a single entry and a single exit point. [1] : 317  (Nowadays a process like this would fall under the umbrella term of refactoring.) All structured programs evidently have an essential complexity of 1 as defined by McCabe because they can all be iteratively reduced to a single call to a top-level subroutine. [1] : 318  As McCabe explains in his paper, his essential complexity metric was designed to provide a measure of how far off this ideal (of being completely structured) a given program was. [1] : 317  Thus greater than 1 essential complexity numbers, which can only be obtained for non-structured programs, indicate that they are further away from the structured programming ideal. [1] : 317 

To avoid confusion between various notions of reducibility to structured programs, it's important to note that McCabe's paper briefly discusses and then operates in the context of a 1973 paper by S. Rao Kosaraju, which gave a refinement (or alternative view) of the structured program theorem. The seminal 1966 paper of Böhm and Jacopini showed that all programs can be [re]written using only structured programming constructs, (aka the D structures: sequence, if-then-else, and while-loop), however, in transforming a random program into a structured program additional variables may need to be introduced (and used in the tests) and some code may be duplicated. [3]

In their paper, Böhm and Jacopini conjectured, but did not prove that it was necessary to introduce such additional variables for certain kinds of non-structured programs in order to transform them into structured programs. [4] : 236  An example of program (that we now know) does require such additional variables is a loop with two conditional exits inside it. In order to address the conjecture of Böhm and Jacopini, Kosaraju defined a more restrictive notion of program reduction than the Turing equivalence used by Böhm and Jacopini. Essentially, Kosaraju's notion of reduction imposes, besides the obvious requirement that the two programs must compute the same value (or not finish) given the same inputs, that the two programs must use the same primitive actions and predicates, the latter understood as expressions used in the conditionals. Because of these restrictions, Kosaraju's reduction does not allow the introduction of additional variables; assigning to these variables would create new primitive actions and testing their values would change the predicates used in the conditionals. Using this more restrictive notion of reduction, Kosaraju proved Böhm and Jacopini's conjecture, namely that a loop with two exits cannot be transformed into a structured program without introducing additional variables, but went further and proved that programs containing multi-level breaks (from loops) form a hierarchy, such that one can always find a program with multi-level breaks of depth n that cannot be reduced to a program of multi-level breaks with depth less than n, again without introducing additional variables. [4] [5]

McCabe notes in his paper that in view of Kosaraju's results, he intended to find a way to capture the essential properties of non-structured programs in terms of their control-flow graphs. [1] : 315  He proceeds by first identifying the control-flow graphs corresponding to the smallest non-structured programs (these include branching into a loop, branching out of a loop, and their if-then-else counterparts) which he uses to formulate a theorem analogous to Kuratowski's theorem, and thereafter he introduces his notion of essential complexity in order to give a scale answer ("measure of the structuredness of a program" in his words) rather than a yes/no answer to the question of whether a program's control-flow graph is structured or not. [1] : 315  Finally, the notion of reduction used by McCabe to shrink the CFG is not the same as Kosaraju's notion of reducing flowcharts. The reduction defined on the CFG does not know or care about the program's inputs, it is simply a graph transformation. [6]

For example, the following C program fragment has an essential complexity of 1, because the inner if statement and the for can be reduced, i.e. it is a structured program.

for(i=0;i<3;i++){if(a[i]==0)b[i]+=2;}

The following C program fragment has an essential complexity of four; its CFG is irreducible. The program finds the first row of z which is all zero and puts that index in i; if there is none, it puts -1 in i.

for(i=0;i<m;i++){for(j=0;j<n;j++){if(z[i][j]!=0)gotonon_zero;}gotofound;non_zero:}i=-1;found:

The idea of CFG reducibility by successive collapses of sub-graphs (ultimately to a single node for well-behaved CFGs) is also used in modern compiler optimization. However the notion from structured programming of single-entry and single-exit control structure is replaced with that of natural loop, which is defined as a "single-entry, multiple-exit loop, with only a single branch back to the entry from within it". The areas of the CFG that cannot be reduced to natural loops are called improper regions; these regions end up having a fairly simple definition: multiple-entry, strongly connected components of the CFG. The simplest improper region is thus a loop with two entry points. Multiple exits do not cause analysis problems in modern compilers. Improper regions (multiple-entries into loops) do cause additional difficulties in optimizing code. [7]

See also

Related Research Articles

In theoretical computer science and mathematics, computational complexity theory focuses on classifying computational problems according to their resource usage, and relating these classes to each other. A computational problem is a task solved by a computer. A computation problem is solvable by mechanical application of mathematical steps, such as an algorithm.

Structured programming is a programming paradigm aimed at improving the clarity, quality, and development time of a computer program by making extensive use of the structured control flow constructs of selection (if/then/else) and repetition, block structures, and subroutines.

<span class="mw-page-title-main">Control-flow graph</span> Graphical representation of a computer program or algorithm

In computer science, a control-flow graph (CFG) is a representation, using graph notation, of all paths that might be traversed through a program during its execution. The control-flow graph was discovered by Frances E. Allen, who noted that Reese T. Prosser used boolean connectivity matrices for flow analysis before.

In computer science, control flow is the order in which individual statements, instructions or function calls of an imperative program are executed or evaluated. The emphasis on explicit control flow distinguishes an imperative programming language from a declarative programming language.

Computability theory, also known as recursion theory, is a branch of mathematical logic, computer science, and the theory of computation that originated in the 1930s with the study of computable functions and Turing degrees. The field has since expanded to include the study of generalized computability and definability. In these areas, computability theory overlaps with proof theory and effective descriptive set theory.

In computational complexity theory, the Cook–Levin theorem, also known as Cook's theorem, states that the Boolean satisfiability problem is NP-complete. That is, it is in NP, and any problem in NP can be reduced in polynomial time by a deterministic Turing machine to the Boolean satisfiability problem.

<span class="mw-page-title-main">Strongly connected component</span> Partition of a graph whose components are reachable from all vertices

In the mathematical theory of directed graphs, a graph is said to be strongly connected if every vertex is reachable from every other vertex. The strongly connected components of an arbitrary directed graph form a partition into subgraphs that are themselves strongly connected. It is possible to test the strong connectivity of a graph, or to find its strongly connected components, in linear time (that is, Θ(V + E)).

Data-flow analysis is a technique for gathering information about the possible set of values calculated at various points in a computer program. A program's control-flow graph (CFG) is used to determine those parts of a program to which a particular value assigned to a variable might propagate. The information gathered is often used by compilers when optimizing a program. A canonical example of a data-flow analysis is reaching definitions.

Cyclomatic complexity is a software metric used to indicate the complexity of a program. It is a quantitative measure of the number of linearly independent paths through a program's source code. It was developed by Thomas J. McCabe, Sr. in 1976.

The structured program theorem, also called the Böhm–Jacopini theorem, is a result in programming language theory. It states that a class of control-flow graphs can compute any computable function if it combines subprograms in only three specific ways. These are

  1. Executing one subprogram, and then another subprogram (sequence)
  2. Executing one of two subprograms according to the value of a boolean expression (selection)
  3. Repeatedly executing a subprogram as long as a boolean expression is true (iteration)

In compiler theory, a reaching definition for a given instruction is an earlier instruction whose target variable can reach the given one without an intervening assignment. For example, in the following code:

d1 : y := 3 d2 : x := y

Programming complexity is a term that includes software properties that affect internal interactions. Several commentators distinguish between the terms "complex" and "complicated". Complicated implies being difficult to understand, but ultimately knowable. Complex, by contrast, describes the interactions between entities. As the number of entities increases, the number of interactions between them increases exponentially, making it impossible to know and understand them all. Similarly, higher levels of complexity in software increase the risk of unintentionally interfering with interactions, thus increasing the risk of introducing defects when changing the software. In more extreme cases, it can make modifying the software virtually impossible.

In computational complexity theory, a gadget is a subunit of a problem instance that simulates the behavior of one of the fundamental units of a different computational problem. Gadgets are typically used to construct reductions from one computational problem to another, as part of proofs of NP-completeness or other types of computational hardness. The component design technique is a method for constructing reductions by using gadgets.

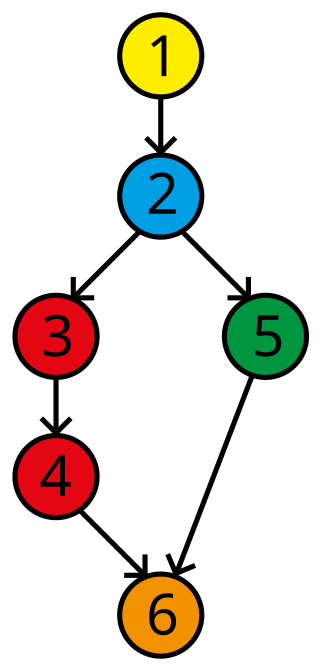
<span class="mw-page-title-main">Decision-to-decision path</span>

A decision-to-decision path, or DD-path, is a path of execution between two decisions. More recent versions of the concept also include the decisions themselves in their own DD-paths.

A signal-flow graph or signal-flowgraph (SFG), invented by Claude Shannon, but often called a Mason graph after Samuel Jefferson Mason who coined the term, is a specialized flow graph, a directed graph in which nodes represent system variables, and branches represent functional connections between pairs of nodes. Thus, signal-flow graph theory builds on that of directed graphs, which includes as well that of oriented graphs. This mathematical theory of digraphs exists, of course, quite apart from its applications.

The #P-completeness of 01-permanent, sometimes known as Valiant's theorem, is a mathematical proof about the permanent of matrices, considered a seminal result in computational complexity theory. In a 1979 scholarly paper, Leslie Valiant proved that the computational problem of computing the permanent of a matrix is #P-hard, even if the matrix is restricted to have entries that are all 0 or 1. In this restricted case, computing the permanent is even #P-complete, because it corresponds to the #P problem of counting the number of permutation matrices one can get by changing ones into zeroes.

A Software Defect Indicator is a pattern that can be found in source code that is strongly correlated with a software defect, an error or omission in the source code of a computer program that may cause it to malfunction. When inspecting the source code of computer programs, it is not always possible to identify defects directly, but there are often patterns, sometimes called anti-patterns, indicating that defects are present.

<span class="mw-page-title-main">Goto</span> One-way control statement in computer programming

Goto is a statement found in many computer programming languages. It performs a one-way transfer of control to another line of code; in contrast a function call normally returns control. The jumped-to locations are usually identified using labels, though some languages use line numbers. At the machine code level, a goto is a form of branch or jump statement, in some cases combined with a stack adjustment. Many languages support the goto statement, and many do not.

<span class="mw-page-title-main">NP-completeness</span> Complexity class

In computational complexity theory, a problem is NP-complete when:

  1. It is a decision problem, meaning that for any input to the problem, the output is either "yes" or "no".
  2. When the answer is "yes", this can be demonstrated through the existence of a short solution.
  3. The correctness of each solution can be verified quickly and a brute-force search algorithm can find a solution by trying all possible solutions.
  4. The problem can be used to simulate every other problem for which we can verify quickly that a solution is correct. In this sense, NP-complete problems are the hardest of the problems to which solutions can be verified quickly. If we could find solutions of some NP-complete problem quickly, we could quickly find the solutions of every other problem to which a given solution can be easily verified.

In software engineering, basis path testing, or structured testing, is a white box method for designing test cases. The method analyzes the control-flow graph of a program to find a set of linearly independent paths of execution. The method normally uses McCabe cyclomatic complexity to determine the number of linearly independent paths and then generates test cases for each path thus obtained. Basis path testing guarantees complete branch coverage, but achieves that without covering all possible paths of the control-flow graph – the latter is usually too costly. Basis path testing has been widely used and studied.

References

  1. 1 2 3 4 5 6 7 McCabe (December 1976). "A Complexity Measure". IEEE Transactions on Software Engineering (4): 308–320. doi:10.1109/tse.1976.233837. S2CID   9116234.
  2. ↑ http://www.mccabe.com/pdf/mccabe-nist235r.pdf [ bare URL PDF ]
  3. ↑ David Anthony Watt; William Findlay (2004). Programming language design concepts. John Wiley & Sons. p. 228. ISBN   978-0-470-85320-7.
  4. 1 2 S. Rao Kosaraju (December 1974). "Analysis of structured programs". Journal of Computer and System Sciences. 9 (3): 232–255. doi:10.1016/S0022-0000(74)80043-7.
  5. ↑ For more modern treatment of the same results see: Kozen, The Böhm–Jacopini Theorem is False, Propositionally
  6. ↑ McCabe footnotes the two definitions of on pages 315 and 317.
  7. ↑ Steven S. Muchnick (1997). Advanced Compiler Design Implementation . Morgan Kaufmann. pp.  196–197 and 215. ISBN   978-1-55860-320-2.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.