Evan O'Neill Kane (physicist)

Last updated

Evan O'Neill Kane (December 23, 1924 – March 23, 2006), known as E. O. Kane in his publications, was an American physicist who established some of the basic understanding of the theory of semiconductors that are now used in consumer and other electronics. He was one of the main developers of the k·p perturbation theory which is used to calculate band structures. [1]

Contents

Ancestry

Kane's great, great uncle, Elisha Kent Kane, was an arctic explorer, writing books in the 1850s about his journeys. His great grandfather, Thomas Leiper Kane, who founded the town of Kane, Pennsylvania, was an American Civil War General. [2] He also helped with the Underground Railroad and successfully urged the Buchanan Administration not to go to war with the Mormons in Salt Lake City. Kane's grandfather, also named Evan O'Neill Kane, was a doctor who was so enamoured of the idea of local anesthesia that he surgically removed his own appendix to show its effectiveness.

Life

Kane was born on December 23, 1924 [3] [4] [5] in Kane, Pennsylvania. His father, Thomas Leiper Kane, died in 1933 of pneumonia. [6] He later moved with his mother and siblings to Daytona Beach, Florida, where he stayed through high school.

Career

Kane was an undergraduate at Princeton University, and interrupted his education to serve in the army during World War II. He graduated from Princeton University in 1948, and went directly to Cornell University to study towards his PhD in physics, which was awarded in 1953 on an experimental project related to vacuum tube technology. Kane then joined the General Electric Research Laboratory in Schenectady, New York. There he began contributing to the theoretical underpinnings of the then-new field of semiconductor research. He published widely in scientific journals. Perhaps his best known paper was published in 1956 on a technique to calculate the structure of solids. [7] This technique is referred to as the k·p method for band structure calculations.

Kane left General Electric in 1959 to join Hughes Aircraft in California and then moved to the Theoretical Physics Department in Bell Laboratories in Murray Hill, New Jersey in 1961. He continued his semiconductor research at Bell Labs, at the interface between experimental and theoretical physics, until AT&T was broken up. He then worked for BellCore until he retired in 1984.[ citation needed ]

Personal life

Kane married Anne Bassler in 1950 in Lancaster, Pennsylvania. They lived together for over 40 years in New Providence, New Jersey, where they raised three children and coauthored one paper. [8]

In 1974, he became ranked second in the country in the 50 and over marathon category. He spent most of the rest of his life working in childcare for infants, toddlers and young children including his grandchildren and church group. He died in 2006 at the age of 81. The cause of death was complications secondary to myeloproliferative disease and myelodysplasia. [3] [5] He had three children. [5]

Kane model

Kane used the k·p perturbation method to determine what became known as the Kane model or Kane Hamiltonian of the structure of energy bands of semiconductors. [9] The Kane Hamiltonian describes the valence and conduction bands in sp3 bonded semiconductors: the group IV, III-V and II-VI semiconductors. This 1957 publication is still prominent in scientific literature and textbooks more than 50 years after its discovery (the paper has about 3377 citations [10] despite the fact that modern citation indexes undercount citations for papers published before the mid-1990s). The model is now often cited via books where it is discussed, most notably in Yu's and Cardona's book, Fundamentals of Semiconductors. [11]

In their book on the k·p method, Voon and Willatzen [12] devote several chapters to explaining Kane models. They note that Kane's quasi-degenerate perturbation theory approach worked well for semiconductors with small band gaps. Kane improved previous valence band models by adding the lowest conduction band. This model was extended later to take into account the non-parabolicity of materials such as gallium arsenide (GaAs). The model explains essentially most of the materials used in semiconductor technology. The theoretical literature describing the electronics and optical responses of these semiconductors all rely heavily on this model, as does the very active field of quantum phenomena in size-limited crystalline structures.

Selected publications

Related Research Articles

<span class="mw-page-title-main">Condensed matter physics</span> Branch of physics

Condensed matter physics is the field of physics that deals with the macroscopic and microscopic physical properties of matter, especially the solid and liquid phases, that arise from electromagnetic forces between atoms and electrons. More generally, the subject deals with condensed phases of matter: systems of many constituents with strong interactions among them. More exotic condensed phases include the superconducting phase exhibited by certain materials at extremely low cryogenic temperatures, the ferromagnetic and antiferromagnetic phases of spins on crystal lattices of atoms, the Bose–Einstein condensates found in ultracold atomic systems, and liquid crystals. Condensed matter physicists seek to understand the behavior of these phases by experiments to measure various material properties, and by applying the physical laws of quantum mechanics, electromagnetism, statistical mechanics, and other physics theories to develop mathematical models and predict the properties of extremely large groups of atoms.

A semiconductor is a material that has an electrical conductivity value falling between that of a conductor, such as copper, and an insulator, such as glass. Its resistivity generally falls as its temperature rises; metals behave in the opposite way. In many cases their conducting properties may be altered in useful ways by introducing impurities ("doping") into the crystal structure. When two differently doped regions exist in the same crystal, a semiconductor junction is created. The behavior of charge carriers, which include electrons, ions, and electron holes, at these junctions is the basis of diodes, transistors, and most modern electronics. Some examples of semiconductors are silicon, germanium, gallium arsenide, and elements near the so-called "metalloid staircase" on the periodic table. After silicon, gallium arsenide is the second-most common semiconductor and is used in laser diodes, solar cells, microwave-frequency integrated circuits, and others. Silicon is a critical element for fabricating most electronic circuits.

<span class="mw-page-title-main">Exciton</span> Quasiparticle which is a bound state of an electron and an electron hole

An electron and an electron hole that are attracted to each other by the Coulomb force can form a bound state called an exciton. It is an electrically neutral quasiparticle that exists mainly in condensed matter, including insulators, semiconductors, some metals, but also in certain atoms, molecules and liquids. The exciton is regarded as an elementary excitation that can transport energy without transporting net electric charge.

A metalloid is a chemical element which has a preponderance of properties in between, or that are a mixture of, those of metals and nonmetals. There is no standard definition of a metalloid and no complete agreement on which elements are metalloids. Despite the lack of specificity, the term remains in use in the literature.

Solid-state physics is the study of rigid matter, or solids, through methods such as solid-state chemistry, quantum mechanics, crystallography, electromagnetism, and metallurgy. It is the largest branch of condensed matter physics. Solid-state physics studies how the large-scale properties of solid materials result from their atomic-scale properties. Thus, solid-state physics forms a theoretical basis of materials science. Along with solid-state chemistry, it also has direct applications in the technology of transistors and semiconductors.

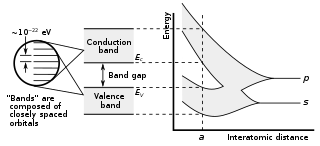
<span class="mw-page-title-main">Band gap</span> Energy range in a solid where no electron states exist

In solid-state physics and solid-state chemistry, a band gap, also called a bandgap or energy gap, is an energy range in a solid where no electronic states exist. In graphs of the electronic band structure of solids, the band gap refers to the energy difference between the top of the valence band and the bottom of the conduction band in insulators and semiconductors. It is the energy required to promote an electron from the valence band to the conduction band. The resulting conduction-band electron are free to move within the crystal lattice and serve as charge carriers to conduct electric current. It is closely related to the HOMO/LUMO gap in chemistry. If the valence band is completely full and the conduction band is completely empty, then electrons cannot move within the solid because there are no available states. If the electrons are not free to move within the crystal lattice, then there is no generated current due to no net charge carrier mobility. However, if some electrons transfer from the valence band to the conduction band, then current can flow. Therefore, the band gap is a major factor determining the electrical conductivity of a solid. Substances having large band gaps are generally insulators, those with small band gaps are semiconductor, and conductors either have very small band gaps or none, because the valence and conduction bands overlap to form a continuous band.

<span class="mw-page-title-main">Electron hole</span> Conceptual opposite of an electron

In physics, chemistry, and electronic engineering, an electron hole is a quasiparticle denoting the lack of an electron at a position where one could exist in an atom or atomic lattice. Since in a normal atom or crystal lattice the negative charge of the electrons is balanced by the positive charge of the atomic nuclei, the absence of an electron leaves a net positive charge at the hole's location.

In solid state physics, a particle's effective mass is the mass that it seems to have when responding to forces, or the mass that it seems to have when interacting with other identical particles in a thermal distribution. One of the results from the band theory of solids is that the movement of particles in a periodic potential, over long distances larger than the lattice spacing, can be very different from their motion in a vacuum. The effective mass is a quantity that is used to simplify band structures by modeling the behavior of a free particle with that mass. For some purposes and some materials, the effective mass can be considered to be a simple constant of a material. In general, however, the value of effective mass depends on the purpose for which it is used, and can vary depending on a number of factors.

The electron affinity (Eea) of an atom or molecule is defined as the amount of energy released when an electron attaches to a neutral atom or molecule in the gaseous state to form an anion.

In solid-state physics, the electronic band structure of a solid describes the range of energy levels that electrons may have within it, as well as the ranges of energy that they may not have.

<span class="mw-page-title-main">Semimetal</span> Metal with a small negative indirect band-gap

A semimetal is a material with a small energy overlap between the bottom of the conduction band and the top of the valence band, but they do not overlap in momentum space. According to electronic band theory, solids can be classified as insulators, semiconductors, semimetals, or metals. In insulators and semiconductors the filled valence band is separated from an empty conduction band by a band gap. For insulators, the magnitude of the band gap is larger than that of a semiconductor. Because of the slight overlap between the conduction and valence bands, semimetals have no band gap and a small density of states at the Fermi level. A metal, by contrast, has an appreciable density of states at the Fermi level because the conduction band is partially filled.

A superlattice is a periodic structure of layers of two materials. Typically, the thickness of one layer is several nanometers. It can also refer to a lower-dimensional structure such as an array of quantum dots or quantum wells.

Per-Olov Löwdin was a Swedish physicist, professor at the University of Uppsala from 1960 to 1983, and in parallel at the University of Florida until 1993.

<span class="mw-page-title-main">Marvin L. Cohen</span> American physicist

Marvin Lou Cohen is an American–Canadian theoretical physicist. He is a physics professor at the University of California, Berkeley. Cohen is a leading expert in the field of condensed matter physics. He is widely known for his seminal work on the electronic structure of solids.

<span class="mw-page-title-main">WIEN2k</span>

The WIEN2k package is a computer program written in Fortran which performs quantum mechanical calculations on periodic solids. It uses the full-potential (linearized) augmented plane-wave and local-orbitals [FP-(L)APW+lo] basis set to solve the Kohn–Sham equations of density functional theory.

In solid-state physics, the k·p perturbation theory is an approximated semi-empirical approach for calculating the band structure and optical properties of crystalline solids. It is pronounced "k dot p", and is also called the "k·p method". This theory has been applied specifically in the framework of the Luttinger–Kohn model, and of the Kane model.

Reflectance difference spectroscopy(RDS) is a spectroscopic technique which measures the difference in reflectance of two beams of light that are shone in normal incident on a surface with different linear polarizations. It is also known as reflectance anisotropy spectroscopy (RAS).

<span class="mw-page-title-main">Valence and conduction bands</span> Electron energy bands which determine the electrical conductivity of a material

In solid-state physics, the valence band and conduction band are the bands closest to the Fermi level, and thus determine the electrical conductivity of the solid. In nonmetals, the valence band is the highest range of electron energies in which electrons are normally present at absolute zero temperature, while the conduction band is the lowest range of vacant electronic states. On a graph of the electronic band structure of a semiconducting material, the valence band is located below the Fermi level, while the conduction band is located above it.

<span class="mw-page-title-main">Elias Burstein</span> American physicist (1917–2017)

Elias Burstein was an American experimental condensed matter physicist whose active career in science spanned seven decades. He is known for his pioneering fundamental research in the optical physics of solids; for writing and editing hundreds of articles and other publications; for bringing together scientists from around the world in international meetings, conferences, and symposia; and for training and mentoring dozens of younger physicists.

References

  1. ↑ Kane, E. O. (January 1, 1966), Willardson, R. K.; Beer, Albert C. (eds.), "Chapter 3 The k •p Method", Semiconductors and Semimetals, Semiconductors and Semimetals, vol. 1, Elsevier, pp. 75–100, retrieved August 15, 2024
  2. ↑ "Kane, Pennsylvania". Allegheny National Forest Visitors Bureau. Retrieved August 15, 2024.
  3. 1 2 "Physics Today Daily Edition Departments".
  4. ↑ "Obituary of Evan O' Neill Kane". Physics Today. 2013. doi:10.1063/pt.4.2301.
  5. 1 2 3 "Bradley & Son Funeral Homes".
  6. ↑ Bowen, Norman R.; Zobell, Albert L.; Jr. "General Thomas L. Kane: the Pioneer". www.churchofjesuschrist.org. Retrieved August 15, 2024.
  7. ↑ Kane, E. O. (1956). "Energy band structure in p-type germanium and silicon". Journal of Physics and Chemistry of Solids. 1 (1–2): 82–99. Bibcode:1956JPCS....1...82K. doi:10.1016/0022-3697(56)90014-2.
  8. ↑ EO Kane and AB Kane, "Direct calculation of Wannier Functions; Si valence bands, Physical Review B, 1978.
  9. ↑ Kane, E. O. (1957). "Band structure of indium antimonide". Journal of Physics and Chemistry of Solids. 1 (4): 249–261. Bibcode:1957JPCS....1..249K. doi:10.1016/0022-3697(57)90013-6.
  10. 1 2 3 4 5 6 7 8 9 10 11 Citation statistics retrieved from Google Scholar, 28 February 2017
  11. ↑ Peter Y. Yu and Manuel Cardona, "Fundamentals of Semiconductors, Physics and Materials Properties, Springer, ISBN   978-3-642-00709-5 (Print) 978-3-642-00710-1 (Online)
  12. ↑ Lok C. Lew Yan Voon and Morten Willatzen, "The k.p Method" Electronic Properties of Semiconductors, Springer, Springer-Verlag Berlin, Heidelberg, 2009. doi : 10.1007/978-3-540-92872-0
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.