
A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral atom contains a single positively charged proton and a single negatively charged electron bound to the nucleus by the Coulomb force. Atomic hydrogen constitutes about 75% of the baryonic mass of the universe.

In astronomy, Kepler's laws of planetary motion, published by Johannes Kepler between 1609 and 1619, describe the orbits of planets around the Sun. The laws modified the heliocentric theory of Nicolaus Copernicus, replacing its circular orbits and epicycles with elliptical trajectories, and explaining how planetary velocities vary. The three laws state that:
- The orbit of a planet is an ellipse with the Sun at one of the two foci.
- A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time.
- The square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit.

In mathematics and physics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace, who first studied its properties. This is often written as

In astronomy, the ecliptic coordinate system is a celestial coordinate system commonly used for representing the apparent positions, orbits, and pole orientations of Solar System objects. Because most planets and many small Solar System bodies have orbits with only slight inclinations to the ecliptic, using it as the fundamental plane is convenient. The system's origin can be the center of either the Sun or Earth, its primary direction is towards the vernal (March) equinox, and it has a right-hand convention. It may be implemented in spherical or rectangular coordinates.
Orbital elements are the parameters required to uniquely identify a specific orbit. In celestial mechanics these elements are considered in two-body systems using a Kepler orbit. There are many different ways to mathematically describe the same orbit, but certain schemes, each consisting of a set of six parameters, are commonly used in astronomy and orbital mechanics.

In mathematics and physical science, spherical harmonics are special functions defined on the surface of a sphere. They are often employed in solving partial differential equations in many scientific fields. A list of the spherical harmonics is available in Table of spherical harmonics.

The equation of time describes the discrepancy between two kinds of solar time. The word equation is used in the medieval sense of "reconciliation of a difference". The two times that differ are the apparent solar time, which directly tracks the diurnal motion of the Sun, and mean solar time, which tracks a theoretical mean Sun with uniform motion along the celestial equator. Apparent solar time can be obtained by measurement of the current position of the Sun, as indicated by a sundial. Mean solar time, for the same place, would be the time indicated by a steady clock set so that over the year its differences from apparent solar time would have a mean of zero.
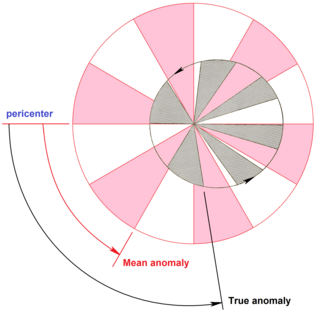
In celestial mechanics, the mean anomaly is the fraction of an elliptical orbit's period that has elapsed since the orbiting body passed periapsis, expressed as an angle which can be used in calculating the position of that body in the classical two-body problem. It is the angular distance from the pericenter which a fictitious body would have if it moved in a circular orbit, with constant speed, in the same orbital period as the actual body in its elliptical orbit.

In celestial mechanics, true anomaly is an angular parameter that defines the position of a body moving along a Keplerian orbit. It is the angle between the direction of periapsis and the current position of the body, as seen from the main focus of the ellipse.
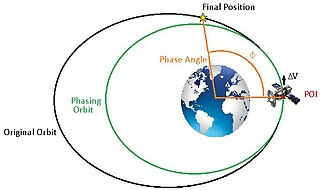
In astrodynamics, orbit phasing is the adjustment of the time-position of spacecraft along its orbit, usually described as adjusting the orbiting spacecraft's true anomaly. Orbital phasing is primarily used in scenarios where a spacecraft in a given orbit must be moved to a different location within the same orbit. The change in position within the orbit is usually defined as the phase angle, ϕ, and is the change in true anomaly required between the spacecraft's current position to the final position.

ʿAbu al-Ḥasan Alāʾ al‐Dīn bin Alī bin Ibrāhīm bin Muhammad bin al-Matam al-Ansari known as Ibn al-Shatir or Ibn ash-Shatir was an Arab astronomer, mathematician and engineer. He worked as muwaqqit in the Umayyad Mosque in Damascus and constructed a sundial for its minaret in 1371/72.
Lunar theory attempts to account for the motions of the Moon. There are many small variations in the Moon's motion, and many attempts have been made to account for them. After centuries of being problematic, lunar motion can now be modeled to a very high degree of accuracy.

On the Sizes and Distances (of the Sun and Moon) (Ancient Greek: Περὶ μεγεθῶν καὶ ἀποστημάτων [ἡλίου καὶ σελήνης], romanized: Perì megethôn kaì apostēmátōn [hēlíou kaì selḗnēs]) is widely accepted as the only extant work written by Aristarchus of Samos, an ancient Greek astronomer who lived circa 310–230 BCE. This work calculates the sizes of the Sun and Moon, as well as their distances from the Earth in terms of Earth's radius.
On Sizes and Distances (of the Sun and Moon) (Περὶ μεγεθῶν καὶ ἀποστημάτων [ἡλίου καὶ σελήνης], Peri megethon kai apostematon) is a text by the ancient Greek astronomer Hipparchus (c. 190 – c. 120 BC) in which approximations are made for the radii of the Sun and the Moon as well as their distances from the Earth. It is not extant, but some of its contents have been preserved in the works of Ptolemy and his commentator Pappus of Alexandria. Several modern historians have attempted to reconstruct the methods of Hipparchus using the available texts.
In astronomy, the variation of the Moon is one of the principal perturbations in the motion of the Moon.
The sunrise equation or sunset equation can be used to derive the time of sunrise or sunset for any solar declination and latitude in terms of local solar time when sunrise and sunset actually occur.

The Moon orbits Earth in the prograde direction and completes one revolution relative to the Vernal Equinox and the stars in about 27.32 days and one revolution relative to the Sun in about 29.53 days. Earth and the Moon orbit about their barycentre, which lies about 4,670 km (2,900 mi) from Earth's centre, forming a satellite system called the Earth–Moon system. On average, the distance to the Moon is about 385,000 km (239,000 mi) from Earth's centre, which corresponds to about 60 Earth radii or 1.282 light-seconds.

The theory of tides is the application of continuum mechanics to interpret and predict the tidal deformations of planetary and satellite bodies and their atmospheres and oceans under the gravitational loading of another astronomical body or bodies.

In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the two most widely separated points of the perimeter. The semi-major axis is the longest semidiameter or one half of the major axis, and thus runs from the centre, through a focus, and to the perimeter. The semi-minor axis of an ellipse or hyperbola is a line segment that is at right angles with the semi-major axis and has one end at the center of the conic section. For the special case of a circle, the lengths of the semi-axes are both equal to the radius of the circle.

In lunar calendars, a lunar month is the time between two successive syzygies of the same type: new moons or full moons. The precise definition varies, especially for the beginning of the month.





















