Exchange-rate pass-through (ERPT) is a measure of how responsive international prices are to changes in exchange rates.
Formally, exchange-rate pass-through is the elasticity of local-currency import prices with respect to the local-currency price of foreign currency. It is often measured as the percentage change, in the local currency, of import prices resulting from a one percent change in the exchange rate between the exporting and importing countries. [1] A change in import prices affects retail and consumer prices. When exchange-rate pass-through is greater, there is more transmission of inflation between countries. [2] Exchange-rate pass-through is also related to the law of one price and purchasing power parity.
Suppose that the US imports widgets from the UK. The widgets cost $10 and £1 costs $1. Then the British Pound appreciates against the dollar and now £1 costs $1.50. Also suppose that the widgets now cost $12.5
There has been a 50% change in the exchange rate and a 25% change in price. The exchange rate pass-through is
For every 1% increase in the exchange rate, there has been a .5% increase in the price of the widgets.
The "standard pass-through regression" [3] is
where is import price, is the exchange rate, is marginal costs, is demand, and denotes a first difference. The exchange-rate pass-through after periods is
Campa and Goldberg (2005) estimated the long-run exchange-rate pass-through to import prices for the following countries, averaging across the countries from which imports came: [2]
| Country | Long-Run Exchange-Rate Pass-Through [2] |
|---|---|
| Australia | 0.69 |
| Canada | 0.68 |
| Switzerland | 0.94 |
| Czech Republic | 0.61 |
| Germany | 0.79 |
| Denmark | 0.68 |
| Spain | 0.56 |
| Finland | 0.82 |
| France | 1.21 |
| United Kingdom | 0.47 |
| Hungary | 0.85 |
| Ireland | 1.37 |
| Iceland | 0.76 |
| Italy | 0.62 |
| Japan | 1.26 |
| Netherlands | 0.77 |
| Norway | 0.79 |
| New Zealand | 0.62 |
| Poland | 0.99 |
| Portugal | 0.88 |
| Sweden | 0.59 |
| USA | 0.41 |
Measurement of exchange-rate pass-through is typically performed using aggregate price indexes. [1] Some studies have examined how firms in different industries or with different production costs differ in their responses to exchange rates. Studies of firm-level differences explain why exchange-rate pass-through is not equal to one [4] and how globalization caused a decrease in exchange-rate pass-through. [5]
In a chemical reaction, chemical equilibrium is the state in which both the reactants and products are present in concentrations which have no further tendency to change with time, so that there is no observable change in the properties of the system. This state results when the forward reaction proceeds at the same rate as the reverse reaction. The reaction rates of the forward and backward reactions are generally not zero, but they are equal. Thus, there are no net changes in the concentrations of the reactants and products. Such a state is known as dynamic equilibrium.
Stimulated emission is the process by which an incoming photon of a specific frequency can interact with an excited atomic electron, causing it to drop to a lower energy level. The liberated energy transfers to the electromagnetic field, creating a new photon with a frequency, polarization, and direction of travel that are all identical to the photons of the incident wave. This is in contrast to spontaneous emission, which occurs at a characteristic rate for each of the atoms/oscillators in the upper energy state regardless of the external electromagnetic field.
In probability theory and statistics, the gamma distribution is a two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-squared distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use:
In mathematical finance, the Greeks are the quantities representing the sensitivity of the price of derivatives such as options to a change in underlying parameters on which the value of an instrument or portfolio of financial instruments is dependent. The name is used because the most common of these sensitivities are denoted by Greek letters. Collectively these have also been called the risk sensitivities, risk measures or hedge parameters.
In thermodynamics, an isentropic process is an idealized thermodynamic process that is both adiabatic and reversible. The work transfers of the system are frictionless, and there is no net transfer of heat or matter. Such an idealized process is useful in engineering as a model of and basis of comparison for real processes. This process is idealized because reversible processes do not occur in reality; thinking of a process as both adiabatic and reversible would show that the initial and final entropies are the same, thus, the reason it is called isentropic. Thermodynamic processes are named based on the effect they would have on the system. Even though in reality it is not necessarily possible to carry out an isentropic process, some may be approximated as such.
The Lotka–Volterra equations, also known as the predator–prey equations, are a pair of first-order nonlinear differential equations, frequently used to describe the dynamics of biological systems in which two species interact, one as a predator and the other as prey. The populations change through time according to the pair of equations:
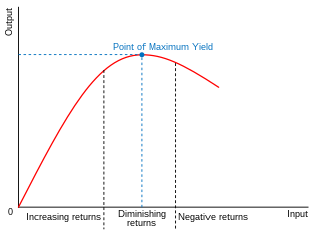
In economics, diminishing returns are the decrease in marginal (incremental) output of a production process as the amount of a single factor of production is incrementally increased, holding all other factors of production equal. The law of diminishing returns states that in productive processes, increasing a factor of production by one unit, while holding all other production factors constant, will at some point return a lower unit of output per incremental unit of input. The law of diminishing returns does not cause a decrease in overall production capabilities, rather it defines a point on a production curve whereby producing an additional unit of output will result in a loss and is known as negative returns. Under diminishing returns, output remains positive, but productivity and efficiency decrease.
Chemiosmosis is the movement of ions across a semipermeable membrane bound structure, down their electrochemical gradient. An important example is the formation of adenosine triphosphate (ATP) by the movement of hydrogen ions (H+) across a membrane during cellular respiration or photosynthesis.
The equilibrium constant of a chemical reaction is the value of its reaction quotient at chemical equilibrium, a state approached by a dynamic chemical system after sufficient time has elapsed at which its composition has no measurable tendency towards further change. For a given set of reaction conditions, the equilibrium constant is independent of the initial analytical concentrations of the reactant and product species in the mixture. Thus, given the initial composition of a system, known equilibrium constant values can be used to determine the composition of the system at equilibrium. However, reaction parameters like temperature, solvent, and ionic strength may all influence the value of the equilibrium constant.
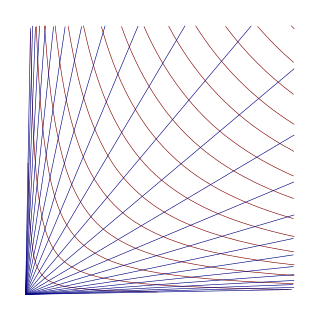
In mathematics, hyperbolic coordinates are a method of locating points in quadrant I of the Cartesian plane
Financial contagion refers to "the spread of market disturbances – mostly on the downside – from one country to the other, a process observed through co-movements in exchange rates, stock prices, sovereign spreads, and capital flows". Financial contagion can be a potential risk for countries who are trying to integrate their financial system with international financial markets and institutions. It helps explain an economic crisis extending across neighboring countries, or even regions.
Interest rate parity is a no-arbitrage condition representing an equilibrium state under which investors interest rates available on bank deposits in two countries. The fact that this condition does not always hold allows for potential opportunities to earn riskless profits from covered interest arbitrage. Two assumptions central to interest rate parity are capital mobility and perfect substitutability of domestic and foreign assets. Given foreign exchange market equilibrium, the interest rate parity condition implies that the expected return on domestic assets will equal the exchange rate-adjusted expected return on foreign currency assets. Investors then cannot earn arbitrage profits by borrowing in a country with a lower interest rate, exchanging for foreign currency, and investing in a foreign country with a higher interest rate, due to gains or losses from exchanging back to their domestic currency at maturity. Interest rate parity takes on two distinctive forms: uncovered interest rate parity refers to the parity condition in which exposure to foreign exchange risk is uninhibited, whereas covered interest rate parity refers to the condition in which a forward contract has been used to cover exchange rate risk. Each form of the parity condition demonstrates a unique relationship with implications for the forecasting of future exchange rates: the forward exchange rate and the future spot exchange rate.
Difference in differences is a statistical technique used in econometrics and quantitative research in the social sciences that attempts to mimic an experimental research design using observational study data, by studying the differential effect of a treatment on a 'treatment group' versus a 'control group' in a natural experiment. It calculates the effect of a treatment on an outcome by comparing the average change over time in the outcome variable for the treatment group to the average change over time for the control group. Although it is intended to mitigate the effects of extraneous factors and selection bias, depending on how the treatment group is chosen, this method may still be subject to certain biases.
A number of different Markov models of DNA sequence evolution have been proposed. These substitution models differ in terms of the parameters used to describe the rates at which one nucleotide replaces another during evolution. These models are frequently used in molecular phylogenetic analyses. In particular, they are used during the calculation of likelihood of a tree and they are used to estimate the evolutionary distance between sequences from the observed differences between the sequences.
In electrochemistry, the Butler–Volmer equation, also known as Erdey-Grúz–Volmer equation, is one of the most fundamental relationships in electrochemical kinetics. It describes how the electrical current through an electrode depends on the voltage difference between the electrode and the bulk electrolyte for a simple, unimolecular redox reaction, considering that both a cathodic and an anodic reaction occur on the same electrode:
In the theory of stochastic processes, a part of the mathematical theory of probability, the variance gamma process (VG), also known as Laplace motion, is a Lévy process determined by a random time change. The process has finite moments distinguishing it from many Lévy processes. There is no diffusion component in the VG process and it is thus a pure jump process. The increments are independent and follow a variance-gamma distribution, which is a generalization of the Laplace distribution.
In electrochemistry, ITIES is an electrochemical interface that is either polarisable or polarised. An ITIES is polarisable if one can change the Galvani potential difference, or in other words the difference of inner potentials between the two adjacent phases, without noticeably changing the chemical composition of the respective phases. An ITIES system is polarised if the distribution of the different charges and redox species between the two phases determines the Galvani potential difference.
In financial econometrics, the Markov-switching multifractal (MSM) is a model of asset returns developed by Laurent E. Calvet and Adlai J. Fisher that incorporates stochastic volatility components of heterogeneous durations. MSM captures the outliers, log-memory-like volatility persistence and power variation of financial returns. In currency and equity series, MSM compares favorably with standard volatility models such as GARCH(1,1) and FIGARCH both in- and out-of-sample. MSM is used by practitioners in the financial industry to forecast volatility, compute value-at-risk, and price derivatives.
Equilibrium chemistry is concerned with systems in chemical equilibrium. The unifying principle is that the free energy of a system at equilibrium is the minimum possible, so that the slope of the free energy with respect to the reaction coordinate is zero. This principle, applied to mixtures at equilibrium provides a definition of an equilibrium constant. Applications include acid–base, host–guest, metal–complex, solubility, partition, chromatography and redox equilibria.
Linda S. Goldberg is an Economist at the Federal Reserve Bank of New York and is currently Senior Vice President in the Research Policy Leadership division. She holds a Ph.D. and M.A. from Princeton University and a B.A. in Mathematics and Economics from the City University of New York.
