Minimax is a decision rule used in artificial intelligence, decision theory, game theory, statistics, and philosophy for minimizing the possible loss for a worst case scenario. When dealing with gains, it is referred to as "maximin" – to maximize the minimum gain. Originally formulated for several-player zero-sum game theory, covering both the cases where players take alternate moves and those where they make simultaneous moves, it has also been extended to more complex games and to general decision-making in the presence of uncertainty.
In statistics, sufficiency is a property of a statistic computed on a sample dataset in relation to a parametric model of the dataset. A sufficient statistic contains all of the information that the dataset provides about the model parameters. It is closely related to the concepts of an ancillary statistic which contains no information about the model parameters, and of a complete statistic which only contains information about the parameters and no ancillary information.
Alpha–beta pruning is a search algorithm that seeks to decrease the number of nodes that are evaluated by the minimax algorithm in its search tree. It is an adversarial search algorithm used commonly for machine playing of two-player combinatorial games. It stops evaluating a move when at least one possibility has been found that proves the move to be worse than a previously examined move. Such moves need not be evaluated further. When applied to a standard minimax tree, it returns the same move as minimax would, but prunes away branches that cannot possibly influence the final decision.
In computer science, iterative deepening search or more specifically iterative deepening depth-first search is a state space/graph search strategy in which a depth-limited version of depth-first search is run repeatedly with increasing depth limits until the goal is found. IDDFS is optimal, meaning that it finds the shallowest goal. Since it visits all the nodes in the search tree down to depth before visiting any nodes at depth , the cumulative order in which nodes are first visited is effectively the same as in breadth-first search. However, IDDFS uses much less memory.
In linear algebra and functional analysis, the min-max theorem, or variational theorem, or Courant–Fischer–Weyl min-max principle, is a result that gives a variational characterization of eigenvalues of compact Hermitian operators on Hilbert spaces. It can be viewed as the starting point of many results of similar nature.

The Gauss–Newton algorithm is used to solve non-linear least squares problems, which is equivalent to minimizing a sum of squared function values. It is an extension of Newton's method for finding a minimum of a non-linear function. Since a sum of squares must be nonnegative, the algorithm can be viewed as using Newton's method to iteratively approximate zeroes of the components of the sum, and thus minimizing the sum. In this sense, the algorithm is also an effective method for solving overdetermined systems of equations. It has the advantage that second derivatives, which can be challenging to compute, are not required.
In the field of mathematics, norms are defined for elements within a vector space. Specifically, when the vector space comprises matrices, such norms are referred to as matrix norms. Matrix norms differ from vector norms in that they must also interact with matrix multiplication.
Negamax search is a variant form of minimax search that relies on the zero-sum property of a two-player game.
In mathematics, the resultant of two polynomials is a polynomial expression of their coefficients that is equal to zero if and only if the polynomials have a common root, or, equivalently, a common factor. In some older texts, the resultant is also called the eliminant.
Principal variation search is a negamax algorithm that can be faster than alpha–beta pruning. Like alpha–beta pruning, NegaScout is a directional search algorithm for computing the minimax value of a node in a tree. It dominates alpha–beta pruning in the sense that it will never examine a node that can be pruned by alpha–beta; however, it relies on accurate node ordering to capitalize on this advantage.
MTD(f) is an alpha-beta game tree search algorithm modified to use ‘zero-window’ initial search bounds, and memory (usually a transposition table) to reuse intermediate search results. MTD(f) is a shortened form of MTD(n,f) which stands for Memory-enhanced Test Driver with node ‘n’ and value ‘f’. The efficacy of this paradigm depends on a good initial guess, and the supposition that the final minimax value lies in a narrow window around the guess (which becomes an upper/lower bound for the search from root). The memory structure is used to save an initial guess determined elsewhere.
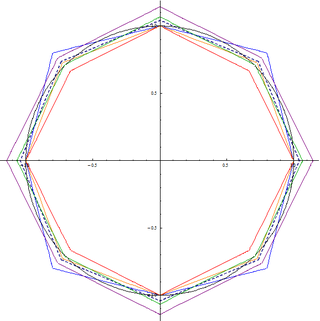
The alpha max plus beta min algorithm is a high-speed approximation of the square root of the sum of two squares. The square root of the sum of two squares, also known as Pythagorean addition, is a useful function, because it finds the hypotenuse of a right triangle given the two side lengths, the norm of a 2-D vector, or the magnitude of a complex number z = a + bi given the real and imaginary parts.
SSS* is a search algorithm, introduced by George Stockman in 1979, that conducts a state space search traversing a game tree in a best-first fashion similar to that of the A* search algorithm.
Collective operations are building blocks for interaction patterns, that are often used in SPMD algorithms in the parallel programming context. Hence, there is an interest in efficient realizations of these operations.
In computer science, the range query problem consists of efficiently answering several queries regarding a given interval of elements within an array. For example, a common task, known as range minimum query, is finding the smallest value inside a given range within a list of numbers.
In coding theory, list decoding is an alternative to unique decoding of error-correcting codes in the presence of many errors. If a code has relative distance , then it is possible in principle to recover an encoded message when up to fraction of the codeword symbols are corrupted. But when error rate is greater than , this will not in general be possible. List decoding overcomes that issue by allowing the decoder to output a short list of messages that might have been encoded. List decoding can correct more than fraction of errors.
In mathematics, the mean (topological) dimension of a topological dynamical system is a non-negative extended real number that is a measure of the complexity of the system. Mean dimension was first introduced in 1999 by Gromov. Shortly after it was developed and studied systematically by Lindenstrauss and Weiss. In particular they proved the following key fact: a system with finite topological entropy has zero mean dimension. For various topological dynamical systems with infinite topological entropy, the mean dimension can be calculated or at least bounded from below and above. This allows mean dimension to be used to distinguish between systems with infinite topological entropy. Mean dimension is also related to the problem of embedding topological dynamical systems in shift spaces.
Best node search (BNS), originally known as fuzzified game tree search, is a minimax search algorithm, developed in 2011. The idea is that the knowledge that one subtree is relatively better than some other(s) may be propagated sooner than the absolute value of minimax for that subtree. Then a repetitive search narrows until a particular node is shown to be relatively best.
Graph cut optimization is a combinatorial optimization method applicable to a family of functions of discrete variables, named after the concept of cut in the theory of flow networks. Thanks to the max-flow min-cut theorem, determining the minimum cut over a graph representing a flow network is equivalent to computing the maximum flow over the network. Given a pseudo-Boolean function , if it is possible to construct a flow network with positive weights such that














