Definition
A field is an algebraic structure composed of a set of elements, F, two binary operations, addition (+) such that F forms an abelian group with identity 0F and multiplication (·), such that F excluding 0F forms an abelian group under multiplication with identity 1F, and such that multiplication is distributive over addition, that is for any elements a, b, c in F, one has a · (b + c) = (a · b) + (a · c). If there is also a function E that maps F into F, and such that for every a and b in F one has

then F is called an exponential field, and the function E is called an exponential function on F. [1] Thus an exponential function on a field is a homomorphism between the additive group of F and its multiplicative group.
Trivial exponential function
There is a trivial exponential function on any field, namely the map that sends every element to the identity element of the field under multiplication. Thus every field is trivially also an exponential field, so the cases of interest to mathematicians occur when the exponential function is non-trivial.
Exponential fields are sometimes required to have characteristic zero as the only exponential function on a field with nonzero characteristic is the trivial one. [2] To see this first note that for any element x in a field with characteristic p > 0,

Hence, taking into account the Frobenius endomorphism,

And so E(x) = 1 for every x. [3]
Exponential rings
The underlying set F may not be required to be a field but instead allowed to simply be a ring, R, and concurrently the exponential function is relaxed to be a homomorphism from the additive group in R to the multiplicative group of units in R. The resulting object is called an exponential ring. [2]
An example of an exponential ring with a nontrivial exponential function is the ring of integers Z equipped with the function E which takes the value +1 at even integers and −1 at odd integers, i.e., the function  This exponential function, and the trivial one, are the only two functions on Z that satisfy the conditions. [5]
This exponential function, and the trivial one, are the only two functions on Z that satisfy the conditions. [5]

In mathematics, an associative algebraA is an algebraic structure with compatible operations of addition, multiplication, and a scalar multiplication by elements in some field K. The addition and multiplication operations together give A the structure of a ring; the addition and scalar multiplication operations together give A the structure of a vector space over K. In this article we will also use the term K-algebra to mean an associative algebra over the field K. A standard first example of a K-algebra is a ring of square matrices over a field K, with the usual matrix multiplication.
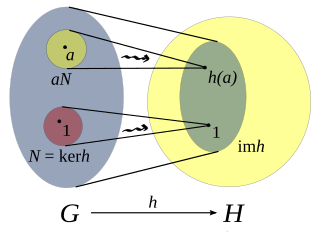
In mathematics, given two groups, (G, ∗) and (H, ·), a group homomorphism from (G, ∗) to (H, ·) is a function h : G → H such that for all u and v in G it holds that
In algebra, a homomorphism is a structure-preserving map between two algebraic structures of the same type. The word homomorphism comes from the Ancient Greek language: ὁμός meaning "same" and μορφή meaning "form" or "shape". However, the word was apparently introduced to mathematics due to a (mis)translation of German ähnlich meaning "similar" to ὁμός meaning "same". The term "homomorphism" appeared as early as 1892, when it was attributed to the German mathematician Felix Klein (1849–1925).

In ring theory, a branch of abstract algebra, a ring homomorphism is a structure-preserving function between two rings. More explicitly, if R and S are rings, then a ring homomorphism is a function f : R → S such that f is:

In mathematics, rings are algebraic structures that generalize fields: multiplication need not be commutative and multiplicative inverses need not exist. In other words, a ring is a set equipped with two binary operations satisfying properties analogous to those of addition and multiplication of integers. Ring elements may be numbers such as integers or complex numbers, but they may also be non-numerical objects such as polynomials, square matrices, functions, and power series.

Algebraic number theory is a branch of number theory that uses the techniques of abstract algebra to study the integers, rational numbers, and their generalizations. Number-theoretic questions are expressed in terms of properties of algebraic objects such as algebraic number fields and their rings of integers, finite fields, and function fields. These properties, such as whether a ring admits unique factorization, the behavior of ideals, and the Galois groups of fields, can resolve questions of primary importance in number theory, like the existence of solutions to Diophantine equations.
In mathematics, an algebra over a field is a vector space equipped with a bilinear product. Thus, an algebra is an algebraic structure consisting of a set together with operations of multiplication and addition and scalar multiplication by elements of a field and satisfying the axioms implied by "vector space" and "bilinear".
In algebra, a valuation is a function on a field that provides a measure of the size or multiplicity of elements of the field. It generalizes to commutative algebra the notion of size inherent in consideration of the degree of a pole or multiplicity of a zero in complex analysis, the degree of divisibility of a number by a prime number in number theory, and the geometrical concept of contact between two algebraic or analytic varieties in algebraic geometry. A field with a valuation on it is called a valued field.
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring, and its basis is the set of elements of the given group. As a ring, its addition law is that of the free module and its multiplication extends "by linearity" the given group law on the basis. Less formally, a group ring is a generalization of a given group, by attaching to each element of the group a "weighting factor" from a given ring.
In mathematics, the characteristic of a ring R, often denoted char(R), is defined to be the smallest number of times one must use the ring's multiplicative identity (1) in a sum to get the additive identity (0). If this sum never reaches the additive identity the ring is said to have characteristic zero.

Transcendental number theory is a branch of number theory that investigates transcendental numbers, in both qualitative and quantitative ways.

In mathematics, specifically transcendental number theory, Schanuel's conjecture is a conjecture made by Stephen Schanuel in the 1960s concerning the transcendence degree of certain field extensions of the rational numbers.
In mathematics, and more specifically in abstract algebra, a rng is an algebraic structure satisfying the same properties as a ring, but without assuming the existence of a multiplicative identity. The term rng is meant to suggest that it is a ring without i, that is, without the requirement for an identity element.
In mathematics, a Drinfeld module is roughly a special kind of module over a ring of functions on a curve over a finite field, generalizing the Carlitz module. Loosely speaking, they provide a function field analogue of complex multiplication theory. A shtuka is a sort of generalization of a Drinfeld module, consisting roughly of a vector bundle over a curve, together with some extra structure identifying a "Frobenius twist" of the bundle with a "modification" of it.
In mathematics, a Pfister form is a particular kind of quadratic form, introduced by Albrecht Pfister in 1965. In what follows, quadratic forms are considered over a field F of characteristic not 2. For a natural number n, an n-fold Pfister form over F is a quadratic form of dimension 2n that can be written as a tensor product of quadratic forms
In mathematics, exponential polynomials are functions on fields, rings, or abelian groups that take the form of polynomials in a variable and an exponential function.
In mathematics, Pfaffian functions are a certain class of functions whose derivative can be written in terms of the original function. They were originally introduced by Askold Khovanskii in the 1970s, but are named after German mathematician Johann Pfaff.
In model theory, Tarski's exponential function problem asks whether the theory of the real numbers together with the exponential function is decidable. Alfred Tarski had previously shown that the theory of the real numbers is decidable.
In mathematics, Wilkie's theorem is a result by Alex Wilkie about the theory of ordered fields with an exponential function, or equivalently about the geometric nature of exponential varieties.
In mathematics, an ordered exponential field is an ordered field together with a function which generalises the idea of exponential functions on the ordered field of real numbers.






