Related Research Articles
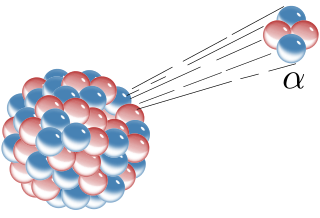
Alpha decay or α-decay is a type of radioactive decay in which an atomic nucleus emits an alpha particle and thereby transforms or 'decays' into a different atomic nucleus, with a mass number that is reduced by four and an atomic number that is reduced by two. An alpha particle is identical to the nucleus of a helium-4 atom, which consists of two protons and two neutrons. It has a charge of +2 e and a mass of 4 u. For example, uranium-238 decays to form thorium-234.
Computational chemistry is a branch of chemistry that uses computer simulation to assist in solving chemical problems. It uses methods of theoretical chemistry, incorporated into computer programs, to calculate the structures and properties of molecules, groups of molecules, and solids. It is essential because, apart from relatively recent results concerning the hydrogen molecular ion, the quantum many-body problem cannot be solved analytically, much less in closed form. While computational results normally complement the information obtained by chemical experiments, it can in some cases predict hitherto unobserved chemical phenomena. It is widely used in the design of new drugs and materials.
Nuclear physics is the field of physics that studies atomic nuclei and their constituents and interactions, in addition to the study of other forms of nuclear matter.
The following outline is provided as an overview of and topical guide to physics:
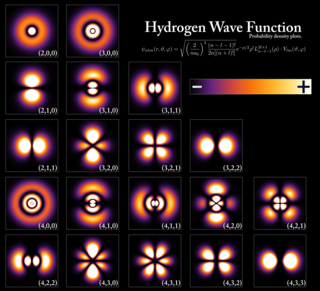
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science.
Statistical physics is a branch of physics that evolved from a foundation of statistical mechanics, which uses methods of probability theory and statistics, and particularly the mathematical tools for dealing with large populations and approximations, in solving physical problems. It can describe a wide variety of fields with an inherently stochastic nature. Its applications include many problems in the fields of physics, biology, chemistry, and neuroscience. Its main purpose is to clarify the properties of matter in aggregate, in terms of physical laws governing atomic motion.
Atomic, molecular, and optical physics (AMO) is the study of matter-matter and light-matter interactions; at the scale of one or a few atoms and energy scales around several electron volts. The three areas are closely interrelated. AMO theory includes classical, semi-classical and quantum treatments. Typically, the theory and applications of emission, absorption, scattering of electromagnetic radiation (light) from excited atoms and molecules, analysis of spectroscopy, generation of lasers and masers, and the optical properties of matter in general, fall into these categories.

In mathematics and applied mathematics, perturbation theory comprises methods for finding an approximate solution to a problem, by starting from the exact solution of a related, simpler problem. A critical feature of the technique is a middle step that breaks the problem into "solvable" and "perturbative" parts. In perturbation theory, the solution is expressed as a power series in a small parameter . The first term is the known solution to the solvable problem. Successive terms in the series at higher powers of usually become smaller. An approximate 'perturbation solution' is obtained by truncating the series, usually by keeping only the first two terms, the solution to the known problem and the 'first order' perturbation correction.
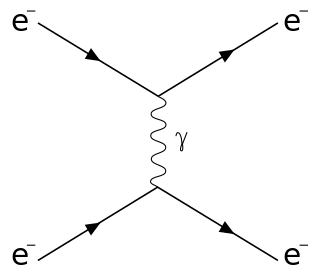
Scattering is a term used in physics to describe a wide range of physical processes where moving particles or radiation of some form, such as light or sound, are forced to deviate from a straight trajectory by localized non-uniformities in the medium through which they pass. In conventional use, this also includes deviation of reflected radiation from the angle predicted by the law of reflection. Reflections of radiation that undergo scattering are often called diffuse reflections and unscattered reflections are called specular (mirror-like) reflections. Originally, the term was confined to light scattering. As more "ray"-like phenomena were discovered, the idea of scattering was extended to them, so that William Herschel could refer to the scattering of "heat rays" in 1800. John Tyndall, a pioneer in light scattering research, noted the connection between light scattering and acoustic scattering in the 1870s. Near the end of the 19th century, the scattering of cathode rays and X-rays was observed and discussed. With the discovery of subatomic particles and the development of quantum theory in the 20th century, the sense of the term became broader as it was recognized that the same mathematical frameworks used in light scattering could be applied to many other phenomena.
The many-body problem is a general name for a vast category of physical problems pertaining to the properties of microscopic systems made of many interacting particles. Microscopic here implies that quantum mechanics has to be used to provide an accurate description of the system. Many can be anywhere from three to infinity, although three- and four-body systems can be treated by specific means and are thus sometimes separately classified as few-body systems.
In physics, quasiparticles and collective excitations are closely related emergent phenomena arising when a microscopically complicated system such as a solid behaves as if it contained different weakly interacting particles in vacuum.

Helium-4 is a stable isotope of the element helium. It is by far the more abundant of the two naturally occurring isotopes of helium, making up about 99.99986% of the helium on Earth. Its nucleus is identical to an alpha particle, and consists of two protons and two neutrons.
The old quantum theory is a collection of results from the years 1900–1925 which predate modern quantum mechanics. The theory was never complete or self-consistent, but was rather a set of heuristic corrections to classical mechanics. The theory is now understood as the semi-classical approximation to modern quantum mechanics. The main and final accomplishments of the old quantum theory were the determination of the modern form of the periodic table by Edmund Stoner and the Pauli Exclusion Principle which were both premised on the Arnold Sommerfeld enhancements to the Bohr model of the atom.

A three-body force is a force that does not exist in a system of two objects but appears in a three-body system. In general, if the behaviour of a system of more than two objects cannot be described by the two-body interactions between all possible pairs, as a first approximation, the deviation is mainly due to a three-body force.
The Faddeev equations, named after their inventor Ludvig Faddeev, are equations that describe, at once, all the possible exchanges/interactions in a system of three particles in a fully quantum mechanical formulation. They can be solved iteratively.
The Lippmann–Schwinger equation is one of the most used equations to describe particle collisions – or, more precisely, scattering – in quantum mechanics. It may be used in scattering of molecules, atoms, neutrons, photons or any other particles and is important mainly in atomic, molecular, and optical physics, nuclear physics and particle physics, but also for seismic scattering problems in geophysics. It relates the scattered wave function with the interaction that produces the scattering and therefore allows calculation of the relevant experimental parameters.
Asım Orhan Barut was a Turkish-American theoretical physicist.
The history of quantum mechanics is a fundamental part of the history of modern physics. Quantum mechanics' history, as it interlaces with the history of quantum chemistry, began essentially with a number of different scientific discoveries: the 1838 discovery of cathode rays by Michael Faraday; the 1859–60 winter statement of the black-body radiation problem by Gustav Kirchhoff; the 1877 suggestion by Ludwig Boltzmann that the energy states of a physical system could be discrete; the discovery of the photoelectric effect by Heinrich Hertz in 1887; and the 1900 quantum hypothesis by Max Planck that any energy-radiating atomic system can theoretically be divided into a number of discrete "energy elements" ε such that each of these energy elements is proportional to the frequency ν with which each of them individually radiate energy, as defined by the following formula:
Physics is a scientific discipline that seeks to construct and experimentally test theories of the physical universe. These theories vary in their scope and can be organized into several distinct branches, which are outlined in this article.
Michał Gryziński was a Polish nuclear physicist, plasma physics specialist and the founder of the free-fall atomic model, an alternative theoretical formulation, a classical approximation asking for trajectories of electron averaging to probability densities described by quantum mechanics.
References
- L.D. Faddeev, S.P. Merkuriev, Quantum Scattering Theory for Several Particle Systems, Springer, August 31, 1993, ISBN 978-0-7923-2414-0.
- M. Schulz et al., Three-Dimensional Imaging of Atomic Four-Body Processes, Nature 422, 48 (2003)
- Erich Schmid, Horst Ziegelmann, The quantum mechanical three-body problem, University of California, 1974
- В.Б. Беляев (V.B. Belyaev), "Лекции по теории малочастичных систем" (Lectures on the theory of few-body systems), М., Энергоатом из дат (Energoatomizdat, Moscow), 1986