
Quantum mechanics is a fundamental theory in physics that describes the behavior of nature at and below the scale of atoms. It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science.
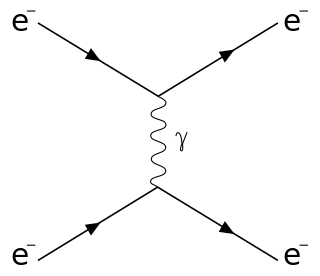
Scattering is a term used in physics to describe a wide range of physical processes where moving particles or radiation of some form, such as light or sound, are forced to deviate from a straight trajectory by localized non-uniformities in the medium through which they pass. In conventional use, this also includes deviation of reflected radiation from the angle predicted by the law of reflection. Reflections of radiation that undergo scattering are often called diffuse reflections and unscattered reflections are called specular (mirror-like) reflections. Originally, the term was confined to light scattering. As more "ray"-like phenomena were discovered, the idea of scattering was extended to them, so that William Herschel could refer to the scattering of "heat rays" in 1800. John Tyndall, a pioneer in light scattering research, noted the connection between light scattering and acoustic scattering in the 1870s. Near the end of the 19th century, the scattering of cathode rays and X-rays was observed and discussed. With the discovery of subatomic particles and the development of quantum theory in the 20th century, the sense of the term became broader as it was recognized that the same mathematical frameworks used in light scattering could be applied to many other phenomena.
In physics, screening is the damping of electric fields caused by the presence of mobile charge carriers. It is an important part of the behavior of charge-carrying fluids, such as ionized gases, electrolytes, and charge carriers in electronic conductors . In a fluid, with a given permittivity ε, composed of electrically charged constituent particles, each pair of particles interact through the Coulomb force as
Density-functional theory (DFT) is a computational quantum mechanical modelling method used in physics, chemistry and materials science to investigate the electronic structure of many-body systems, in particular atoms, molecules, and the condensed phases. Using this theory, the properties of a many-electron system can be determined by using functionals, i.e. functions of another function. In the case of DFT, these are functionals of the spatially dependent electron density. DFT is among the most popular and versatile methods available in condensed-matter physics, computational physics, and computational chemistry.
The many-body problem is a general name for a vast category of physical problems pertaining to the properties of microscopic systems made of many interacting particles. Microscopic here implies that quantum mechanics has to be used to provide an accurate description of the system. Many can be anywhere from three to infinity, although three- and four-body systems can be treated by specific means and are thus sometimes separately classified as few-body systems.
In theoretical physics and mathematical physics, analytical mechanics, or theoretical mechanics is a collection of closely related formulations of classical mechanics. Analytical mechanics uses scalar properties of motion representing the system as a whole—usually its kinetic energy and potential energy. The equations of motion are derived from the scalar quantity by some underlying principle about the scalar's variation.
In quantum mechanics, angular momentum coupling is the procedure of constructing eigenstates of total angular momentum out of eigenstates of separate angular momenta. For instance, the orbit and spin of a single particle can interact through spin–orbit interaction, in which case the complete physical picture must include spin–orbit coupling. Or two charged particles, each with a well-defined angular momentum, may interact by Coulomb forces, in which case coupling of the two one-particle angular momenta to a total angular momentum is a useful step in the solution of the two-particle Schrödinger equation. In both cases the separate angular momenta are no longer constants of motion, but the sum of the two angular momenta usually still is. Angular momentum coupling in atoms is of importance in atomic spectroscopy. Angular momentum coupling of electron spins is of importance in quantum chemistry. Also in the nuclear shell model angular momentum coupling is ubiquitous.
The Schrödinger–Newton equation, sometimes referred to as the Newton–Schrödinger or Schrödinger–Poisson equation, is a nonlinear modification of the Schrödinger equation with a Newtonian gravitational potential, where the gravitational potential emerges from the treatment of the wave function as a mass density, including a term that represents interaction of a particle with its own gravitational field. The inclusion of a self-interaction term represents a fundamental alteration of quantum mechanics. It can be written either as a single integro-differential equation or as a coupled system of a Schrödinger and a Poisson equation. In the latter case it is also referred to in the plural form.

A three-body force is a force that does not exist in a system of two objects but appears in a three-body system. In general, if the behaviour of a system of more than two objects cannot be described by the two-body interactions between all possible pairs, as a first approximation, the deviation is mainly due to a three-body force.

The nuclear force is a force that acts between hadrons, most commonly observed between protons and neutrons of atoms. Neutrons and protons, both nucleons, are affected by the nuclear force almost identically. Since protons have charge +1 e, they experience an electric force that tends to push them apart, but at short range the attractive nuclear force is strong enough to overcome the electrostatic force. The nuclear force binds nucleons into atomic nuclei.

In the physics of gauge theories, gauge fixing denotes a mathematical procedure for coping with redundant degrees of freedom in field variables. By definition, a gauge theory represents each physically distinct configuration of the system as an equivalence class of detailed local field configurations. Any two detailed configurations in the same equivalence class are related by a certain transformation, equivalent to a shear along unphysical axes in configuration space. Most of the quantitative physical predictions of a gauge theory can only be obtained under a coherent prescription for suppressing or ignoring these unphysical degrees of freedom.
In mechanics, a few-body system consists of a small number of well-defined structures or point particles.
The Lippmann–Schwinger equation is one of the most used equations to describe particle collisions – or, more precisely, scattering – in quantum mechanics. It may be used in scattering of molecules, atoms, neutrons, photons or any other particles and is important mainly in atomic, molecular, and optical physics, nuclear physics and particle physics, but also for seismic scattering problems in geophysics. It relates the scattered wave function with the interaction that produces the scattering and therefore allows calculation of the relevant experimental parameters.
Asım Orhan Barut was a Turkish-American theoretical physicist.
In atomic, molecular, and optical physics and quantum chemistry, the molecular Hamiltonian is the Hamiltonian operator representing the energy of the electrons and nuclei in a molecule. This operator and the associated Schrödinger equation play a central role in computational chemistry and physics for computing properties of molecules and aggregates of molecules, such as thermal conductivity, specific heat, electrical conductivity, optical, and magnetic properties, and reactivity.

Understanding the structure of the atomic nucleus is one of the central challenges in nuclear physics.
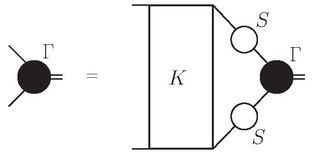
The Bethe–Salpeter equation describes the bound states of a two-body (particles) quantum field theoretical system in a relativistically covariant formalism. The equation was first published in 1950 at the end of a paper by Yoichiro Nambu, but without derivation.
Physics is a scientific discipline that seeks to construct and experimentally test theories of the physical universe. These theories vary in their scope and can be organized into several distinct branches, which are outlined in this article.

In physics, a field is a physical quantity, represented by a scalar, vector, or tensor, that has a value for each point in space and time. For example, on a weather map, the surface temperature is described by assigning a number to each point on the map; the temperature can be considered at a certain point in time or over some interval of time, to study the dynamics of temperature change. A surface wind map, assigning an arrow to each point on a map that describes the wind speed and direction at that point, is an example of a vector field, i.e. a 1-dimensional (rank-1) tensor field. Field theories, mathematical descriptions of how field values change in space and time, are ubiquitous in physics. For instance, the electric field is another rank-1 tensor field, while electrodynamics can be formulated in terms of two interacting vector fields at each point in spacetime, or as a single-rank 2-tensor field.
The Wannier equation describes a quantum mechanical eigenvalue problem in solids where an electron in a conduction band and an electronic vacancy within a valence band attract each other via the Coulomb interaction. For one electron and one hole, this problem is analogous to the Schrödinger equation of the hydrogen atom; and the bound-state solutions are called excitons. When an exciton's radius extends over several unit cells, it is referred to as a Wannier exciton in contrast to Frenkel excitons whose size is comparable with the unit cell. An excited solid typically contains many electrons and holes; this modifies the Wannier equation considerably. The resulting generalized Wannier equation can be determined from the homogeneous part of the semiconductor Bloch equations or the semiconductor luminescence equations.







