Fibonorial

Last updated May 14, 2024

In mathematics, the Fibonorial $n! F$ , also called the Fibonacci factorial, where $n$ is a nonnegative integer, is defined as the product of the first $n$ positive Fibonacci numbers, i.e.

Asymptotic behaviour

The series of fibonorials is asymptotic to a function of the golden ratio $\varphi$ : $n!_{F}\sim C{\frac {\varphi ^{n(n+1)/2}}{5^{n/2}}}$ .

Here the fibonorial constant (also called the fibonacci factorial constant^[1]) $C$ is defined by $C=\prod _{k=1}^{\infty }(1-a^{k})$ , where $a=-{\frac {1}{\varphi ^{2}}}$ and $\varphi$ is the golden ratio.

An approximate truncated value of $C$ is 1.226742010720 (see (sequence A062073 in the OEIS ) for more digits).

Almost-Fibonorial numbers

Almost-Fibonorial numbers: $n! F - 1$ .

Almost-Fibonorial primes: prime numbers among the almost-Fibonorial numbers.

Quasi-Fibonorial numbers

Quasi-Fibonorial numbers: $n! F + 1$ .

Quasi-Fibonorial primes: prime numbers among the quasi-Fibonorial numbers.

Connection with the q-Factorial

The fibonorial can be expressed in terms of the q-factorial and the golden ratio $\varphi ={\frac {1+{\sqrt {5}}}{2}}$ :

n!_{F}=\varphi ^{\binom {n}{2}}\,[n]_{-\varphi ^{-2}}!.

Sequences

OEIS: A003266 Product of first $n$ nonzero Fibonacci numbers $F (1), ..., F (n)$ .

OEIS: A059709 and OEIS: A053408 for $n$ such that $n! F - 1$ and $n! F + 1$ are primes, respectively.

Related Research Articles

In mathematics, the Fibonacci sequence is a sequence in which each number is the sum of the two preceding ones. Numbers that are part of the Fibonacci sequence are known as Fibonacci numbers, commonly denoted $F n$ . The sequence commonly starts from 0 and 1, although some authors start the sequence from 1 and 1 or sometimes from 1 and 2. Starting from 0 and 1, the sequence begins

In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities $and with, is in a golden ratio to if$

In mathematics, the discriminant of a polynomial is a quantity that depends on the coefficients and allows deducing some properties of the roots without computing them. More precisely, it is a polynomial function of the coefficients of the original polynomial. The discriminant is widely used in polynomial factoring, number theory, and algebraic geometry.

In mathematics, a recurrence relation is an equation according to which the $th term of a sequence of numbers is equal to some combination of the previous terms. Often, only previous terms of the sequence appear in the equation, for a parameter that is independent of; this number is called the order of the relation. If the values of the first numbers in the sequence have been given, the rest of the sequence can be calculated by repeatedly applying the equation.$

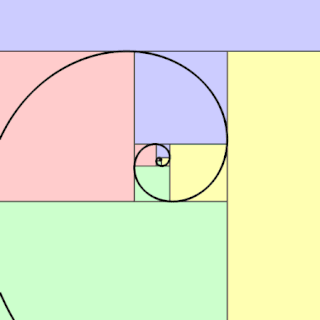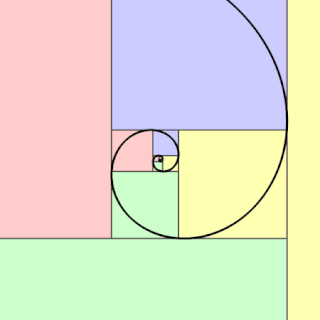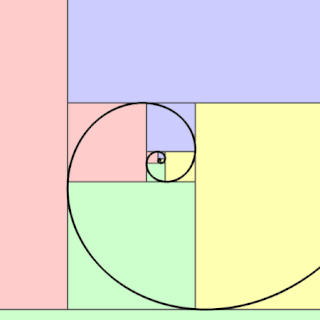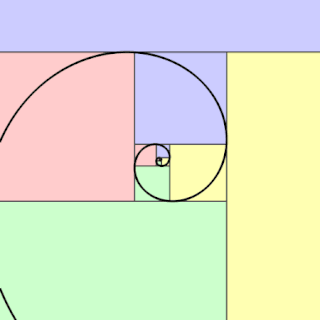
In geometry, a golden spiral is a logarithmic spiral whose growth factor is $φ$ , the golden ratio. That is, a golden spiral gets wider by a factor of $φ$ for every quarter turn it makes.

In mathematics, the falling factorial is defined as the polynomial

The Lucas sequence is an integer sequence named after the mathematician François Édouard Anatole Lucas (1842–1891), who studied both that sequence and the closely related Fibonacci sequence. Individual numbers in the Lucas sequence are known as Lucas numbers. Lucas numbers and Fibonacci numbers form complementary instances of Lucas sequences.

In mathematics, the random Fibonacci sequence is a stochastic analogue of the Fibonacci sequence defined by the recurrence relation $, where the signs + or - are chosen at random with equal probability, independently for different . By a theorem of Harry Kesten and Hillel Furstenberg, random recurrent sequences of this kind grow at a certain exponential rate, but it is difficult to compute the rate explicitly. In 1999, Divakar Viswanath showed that the growth rate of the random Fibonacci sequence is equal to 1.1319882487943..., a mathematical constant that was later named Viswanath's constant.$

In mathematics, and more particularly in number theory, primorial, denoted by "#", is a function from natural numbers to natural numbers similar to the factorial function, but rather than successively multiplying positive integers, the function only multiplies prime numbers.

A Fibonacci word is a specific sequence of binary digits. The Fibonacci word is formed by repeated concatenation in the same way that the Fibonacci numbers are formed by repeated addition.

In mathematics, the plastic ratio is a geometrical proportion close to $53/40$ . Its true value is the real solution of the equation $x 3 = x + 1.$

In number theory, the Dedekind psi function is the multiplicative function on the positive integers defined by

In mathematics, the Fibonacci numbers form a sequence defined recursively by:

In the mathematical field of combinatorics, the q-Pochhammer symbol, also called the q-shifted factorial, is the product

The square root of 5 is the positive real number that, when multiplied by itself, gives the prime number 5. It is more precisely called the principal square root of 5, to distinguish it from the negative number with the same property. This number appears in the fractional expression for the golden ratio. It can be denoted in surd form as:

In mathematics, the Fibonomial coefficients or Fibonacci-binomial coefficients are defined as

In mathematics, the Wythoff array is an infinite matrix of integers derived from the Fibonacci sequence and named after Dutch mathematician Willem Abraham Wythoff. Every positive integer occurs exactly once in the array, and every integer sequence defined by the Fibonacci recurrence can be derived by shifting a row of the array.

A mathematical constant is a key number whose value is fixed by an unambiguous definition, often referred to by a special symbol, or by mathematicians' names to facilitate using it across multiple mathematical problems. Constants arise in many areas of mathematics, with constants such as $e$ and $π$ occurring in such diverse contexts as geometry, number theory, statistics, and calculus.

In mathematics, the supergolden ratio is a geometrical proportion close to $85/58$ . Its true value is the real solution of the equation $x 3 = x 2 + 1.$

In number theory, the totient summatory function $is a summatory function of Euler's totient function defined by:$

References

↑ W., Weisstein, Eric. "Fibonacci Factorial Constant". mathworld.wolfram.com. Retrieved 2018-10-25.{{cite web}}: CS1 maint: multiple names: authors list (link)

Weisstein, Eric W. "Fibonorial". MathWorld .

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] W., Weisstein, Eric. "Fibonacci Factorial Constant". mathworld.wolfram.com. Retrieved 2018-10-25.{{cite web}}: CS1 maint: multiple names: authors list (link)

[1]