Notes
- ↑ Harris' motivation for the distinction is to distinguish between an odd-length data sequence with the indices which he calls the finite Fourier transform data window, and a sequence on which is the DFT data window.
In mathematics the finite Fourier transform may refer to either
or
or

In mathematics, the discrete Fourier transform (DFT) converts a finite sequence of equally-spaced samples of a function into a same-length sequence of equally-spaced samples of the discrete-time Fourier transform (DTFT), which is a complex-valued function of frequency. The interval at which the DTFT is sampled is the reciprocal of the duration of the input sequence. An inverse DFT (IDFT) is a Fourier series, using the DTFT samples as coefficients of complex sinusoids at the corresponding DTFT frequencies. It has the same sample-values as the original input sequence. The DFT is therefore said to be a frequency domain representation of the original input sequence. If the original sequence spans all the non-zero values of a function, its DTFT is continuous, and the DFT provides discrete samples of one cycle. If the original sequence is one cycle of a periodic function, the DFT provides all the non-zero values of one DTFT cycle.
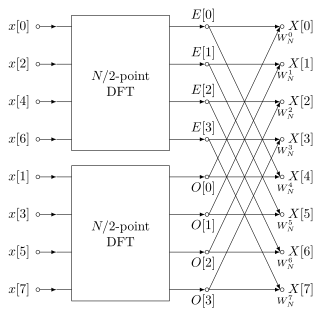
A fast Fourier transform (FFT) is an algorithm that computes the discrete Fourier transform (DFT) of a sequence, or its inverse (IDFT). Fourier analysis converts a signal from its original domain to a representation in the frequency domain and vice versa. The DFT is obtained by decomposing a sequence of values into components of different frequencies. This operation is useful in many fields, but computing it directly from the definition is often too slow to be practical. An FFT rapidly computes such transformations by factorizing the DFT matrix into a product of sparse factors. As a result, it manages to reduce the complexity of computing the DFT from , which arises if one simply applies the definition of DFT, to , where is the data size. The difference in speed can be enormous, especially for long data sets where N may be in the thousands or millions. In the presence of round-off error, many FFT algorithms are much more accurate than evaluating the DFT definition directly or indirectly. There are many different FFT algorithms based on a wide range of published theories, from simple complex-number arithmetic to group theory and number theory.

In mathematics, Fourier analysis is the study of the way general functions may be represented or approximated by sums of simpler trigonometric functions. Fourier analysis grew from the study of Fourier series, and is named after Joseph Fourier, who showed that representing a function as a sum of trigonometric functions greatly simplifies the study of heat transfer.
A discrete cosine transform (DCT) expresses a finite sequence of data points in terms of a sum of cosine functions oscillating at different frequencies. The DCT, first proposed by Nasir Ahmed in 1972, is a widely used transformation technique in signal processing and data compression. It is used in most digital media, including digital images, digital video, digital audio, digital television, digital radio, and speech coding. DCTs are also important to numerous other applications in science and engineering, such as digital signal processing, telecommunication devices, reducing network bandwidth usage, and spectral methods for the numerical solution of partial differential equations.
In mathematics and signal processing, the Z-transform converts a discrete-time signal, which is a sequence of real or complex numbers, into a complex frequency-domain representation.
In mathematics, the discrete sine transform (DST) is a Fourier-related transform similar to the discrete Fourier transform (DFT), but using a purely real matrix. It is equivalent to the imaginary parts of a DFT of roughly twice the length, operating on real data with odd symmetry (since the Fourier transform of a real and odd function is imaginary and odd), where in some variants the input and/or output data are shifted by half a sample.
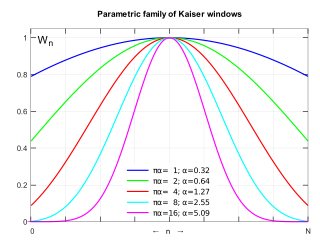
The Kaiser window, also known as the Kaiser–Bessel window, was developed by James Kaiser at Bell Laboratories. It is a one-parameter family of window functions used in finite impulse response filter design and spectral analysis. The Kaiser window approximates the DPSS window which maximizes the energy concentration in the main lobe but which is difficult to compute.
The chirp Z-transform (CZT) is a generalization of the discrete Fourier transform (DFT). While the DFT samples the Z plane at uniformly-spaced points along the unit circle, the chirp Z-transform samples along spiral arcs in the Z-plane, corresponding to straight lines in the S plane. The DFT, real DFT, and zoom DFT can be calculated as special cases of the CZT.
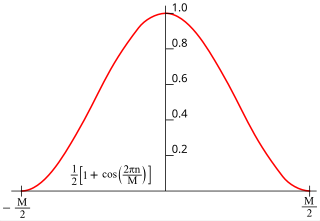
In signal processing and statistics, a window function is a mathematical function that is zero-valued outside of some chosen interval, normally symmetric around the middle of the interval, usually near a maximum in the middle, and usually tapering away from the middle. Mathematically, when another function or waveform/data-sequence is "multiplied" by a window function, the product is also zero-valued outside the interval: all that is left is the part where they overlap, the "view through the window". Equivalently, and in actual practice, the segment of data within the window is first isolated, and then only that data is multiplied by the window function values. Thus, tapering, not segmentation, is the main purpose of window functions.
In signal processing, a finite impulse response (FIR) filter is a filter whose impulse response is of finite duration, because it settles to zero in finite time. This is in contrast to infinite impulse response (IIR) filters, which may have internal feedback and may continue to respond indefinitely.
In signal processing, a periodogram is an estimate of the spectral density of a signal. The term was coined by Arthur Schuster in 1898. Today, the periodogram is a component of more sophisticated methods. It is the most common tool for examining the amplitude vs frequency characteristics of FIR filters and window functions. FFT spectrum analyzers are also implemented as a time-sequence of periodograms.
The Fourier transform of a function of time, s(t), is a complex-valued function of frequency, S(f), often referred to as a frequency spectrum. Any linear time-invariant operation on s(t) produces a new spectrum of the form H(f)•S(f), which changes the relative magnitudes and/or angles (phase) of the non-zero values of S(f). Any other type of operation creates new frequency components that may be referred to as spectral leakage in the broadest sense. Sampling, for instance, produces leakage, which we call aliases of the original spectral component. For Fourier transform purposes, sampling is modeled as a product between s(t) and a Dirac comb function. The spectrum of a product is the convolution between S(f) and another function, which inevitably creates the new frequency components. But the term 'leakage' usually refers to the effect of windowing, which is the product of s(t) with a different kind of function, the window function. Window functions happen to have finite duration, but that is not necessary to create leakage. Multiplication by a time-variant function is sufficient.
In mathematics, the discrete-time Fourier transform (DTFT), also called the finite Fourier transform, is a form of Fourier analysis that is applicable to a sequence of values.
In digital signal processing, downsampling, compression, and decimation are terms associated with the process of resampling in a multi-rate digital signal processing system. Both downsampling and decimation can be synonymous with compression, or they can describe an entire process of bandwidth reduction (filtering) and sample-rate reduction. When the process is performed on a sequence of samples of a signal or a continuous function, it produces an approximation of the sequence that would have been obtained by sampling the signal at a lower rate.

The Hann function is named after the Austrian meteorologist Julius von Hann. It is a window function used to perform Hann smoothing. The function, with length and amplitude is given by:
In mathematics, the discrete Fourier transform over a ring generalizes the discrete Fourier transform (DFT), of a function whose values are commonly complex numbers, over an arbitrary ring.

In signal processing, overlap–save is the traditional name for an efficient way to evaluate the discrete convolution between a very long signal and a finite impulse response (FIR) filter :
In digital signal processing, the term Discrete Fourier series (DFS) is any periodic discrete-time signal comprising harmonically-related discrete real sinusoids or discrete complex exponentials, combined by a weighted summation. A specific example is the inverse discrete Fourier transform.
In applied mathematics, the sliding discrete Fourier transform is a recursive algorithm to compute successive STFTs of input data frames that are a single sample apart (hopsize − 1). The calculation for the sliding DFT is closely related to Goertzel algorithm.