Fixation (population genetics)

Last updated June 18, 2024

In population genetics, fixation is the change in a gene pool from a situation where there exists at least two variants of a particular gene (allele) in a given population to a situation where only one of the alleles remains. That is, the allele becomes fixed. ^[1] In the absence of mutation or heterozygote advantage, any allele must eventually either be lost completely from the population, or fixed, i.e. permanently established at 100% frequency in the population.^[2] Whether a gene will ultimately be lost or fixed is dependent on selection coefficients and chance fluctuations in allelic proportions.^[3] Fixation can refer to a gene in general or particular nucleotide position in the DNA chain (locus).

In the process of substitution, a previously non-existent allele arises by mutation and undergoes fixation by spreading through the population by random genetic drift or positive selection. Once the frequency of the allele is at 100%, i.e. being the only gene variant present in any member, it is said to be "fixed" in the population.^[1]

Similarly, genetic differences between taxa are said to have been fixed in each species.

History

The earliest mention of gene fixation in published works was found in Motoo Kimura's 1962 paper "On Probability of Fixation of Mutant Genes in a Population". In the paper, Kimura uses mathematical techniques to determine the probability of fixation of mutant genes in a population. He showed that the probability of fixation depends on the initial frequency of the allele and the mean and variance of the gene frequency change per generation.^[4]

Probability

Neutral alleles

Under conditions of genetic drift alone, every finite set of genes or alleles has a "coalescent point" at which all descendants converge to a single ancestor (i.e. they 'coalesce'). This fact can be used to derive the rate of gene fixation of a neutral allele (that is, one not under any form of selection) for a population of varying size (provided that it is finite and nonzero). Because the effect of natural selection is stipulated to be negligible, the probability at any given time that an allele will ultimately become fixed at its locus is simply its frequency $p$ in the population at that time. For example, if a population includes allele A with frequency equal to 20%, and allele a with frequency equal to 80%, there is an 80% chance that after an infinite number of generations a will be fixed at the locus (assuming genetic drift is the only operating evolutionary force).

For a diploid population of size N and neutral mutation rate $\mu$ , the initial frequency of a novel mutation is simply 1/(2N), and the number of new mutations per generation is $2N\mu$ . Since the fixation rate is the rate of novel neutral mutation multiplied by their probability of fixation, the overall fixation rate is $2N\mu \times {\frac {1}{2N}}=\mu$ . Thus, the rate of fixation for a mutation not subject to selection is simply the rate of introduction of such mutations.^[5]

Non-neutral alleles

For fixed population sizes, the probability of fixation for a new allele with selective advantage s can be approximated using the theory of branching processes. A population with non-overlapping generations n = 0, 1, 2, 3, ... , and with $X_{n}$ genes (or "individuals") at time n forms a Markov chain under the following assumptions. The introduction of an individual possessing an allele with a selective advantage corresponds to $X_{0}=1$ . The number of offspring of any one individual must follow a fixed distribution and is independently determined. In this framework the generating functions $p_{n}(x)$ for each $X_{n}$ satisfy the recursion relation $p_{n}(x)=p_{1}(p_{n-1}(x))$ and can be used to compute the probabilities $\pi _{n}=P(X_{n}=0)$ of no descendants at time n. It can be shown that $\pi _{n}=p_{1}(\pi _{n-1})$ , and furthermore, that the $\pi _{n}$ converge to a specific value $\pi$ , which is the probability that the individual will have no descendants. The probability of fixation is then $1-\pi \approx 2s/\sigma ^{2}$ since the indefinite survival of the beneficial allele will permit its increase in frequency to a point where selective forces will ensure fixation.

Weakly deleterious mutations can fix in smaller populations through chance, and the probability of fixation will depend on rates of drift (~ $1/N_{e}$ ) and selection (~ $s$ ), where $N_{e}$ is the effective population size. The ratio $N_{e}s$ determines whether selection or drift dominates, and as long as this ratio is not too negative, there will be an appreciable chance that a mildly deleterious allele will fix. For example, in a diploid population of size $N_{e}$ , a deleterious allele with selection coefficient $-s$ has a probability fixation equal to $(1-e^{-2s})/(1-e^{-4N_{e}s})$ . This estimate can be obtained directly from Kimura's 1962 work.^[4] Deleterious alleles with selection coefficients $-s$ satisfying $2N_{e}s\ll 1$ are effectively neutral, and consequently have a probability of fixation approximately equal to $1/2N_{e}$ .

Effect of growing/shrinking populations

Probability of fixation is also influenced by population size changes. For growing populations, selection coefficients are more effective. This means that beneficial alleles are more likely to become fixed, whereas deleterious alleles are more likely to be lost. In populations that are shrinking in size, selection coefficients are not as effective. Thus, there is a higher probability of beneficial alleles being lost and deleterious alleles being fixed. This is because if a beneficial mutation is rare, it can be lost purely due to chance of that individual not having offspring, no matter the selection coefficient. In growing populations, the average individual has a higher expected number of offspring, whereas in shrinking populations the average individual has a lower number of expected offspring. Thus, in growing populations it is more likely that the beneficial allele will be passed on to more individuals in the next generation. This continues until the allele flourishes in the population, and is eventually fixed. However, in a shrinking population it is more likely that the allele may not be passed on, simply because the parents produce no offspring. This would cause even a beneficial mutation to be lost.^[6]

Time

Additionally, research has been done into the average time it takes for a neutral mutation to become fixed. Kimura and Ohta (1969) showed that a new mutation that eventually fixes will spend an average of 4N_e generations as a polymorphism in the population.^[2] Average time to fixation N_e is the effective population size, the number of individuals in an idealised population under genetic drift required to produce an equivalent amount of genetic diversity. Usually the population statistic used to define effective population size is heterozygosity, but others can be used.^[7]

Fixation rates can easily be modeled as well to see how long it takes for a gene to become fixed with varying population sizes and generations. For example, The Biology Project Genetic Drift Simulation allows to model genetic drift and see how quickly the gene for worm color goes to fixation in terms of generations for different population sizes.

Additionally, fixation rates can be modeled using coalescent trees. A coalescent tree traces the descent of alleles of a gene in a population.^[8] It aims to trace back to a single ancestral copy called the most recent common ancestor.^[9]

Examples in research

In 1969, Schwartz at Indiana University was able to artificially induce gene fixation into maize, by subjecting samples to suboptimal conditions. Schwartz located a mutation in a gene called Adh1, which when homozygous causes maize to be unable to produce alcohol dehydrogenase. Schwartz then subjected seeds, with both normal alcohol dehydrogenase activity and no activity, to flooding conditions and observed whether the seeds were able to germinate or not. He found that when subjected to flooding, only seeds with alcohol dehydrogenase activity germinated. This ultimately caused gene fixation of the Adh1 wild type allele. The Adh1 mutation was lost in the experimented population.^[10]

In 2014, Lee, Langley, and Begun conducted another research study related to gene fixation. They focused on Drosophila melanogaster population data and the effects of genetic hitchhiking caused by selective sweeps. Genetic hitchhiking occurs when one allele is strongly selected for and driven to fixation. This causes the surrounding areas to also be driven to fixation, even though they are not being selected for.^[11] By looking at the Drosophila melanogaster population data, Lee et al. found a reduced amount of heterogeneity within 25 base pairs of focal substitutions. They accredit this to small-scale hitchhiking effects. They also found that neighboring fixations that changed amino acid polarities while maintaining the overall polarity of a protein were under stronger selection pressures. Additionally, they found that substitutions in slowly evolving genes were associated with stronger genetic hitchhiking effects.^[12]

Related Research Articles

Genetic drift, also known as random genetic drift, allelic drift or the Wright effect, is the change in the frequency of an existing gene variant (allele) in a population due to random chance.

Small populations can behave differently from larger populations. They are often the result of population bottlenecks from larger populations, leading to loss of heterozygosity and reduced genetic diversity and loss or fixation of alleles and shifts in allele frequencies. A small population is then more susceptible to demographic and genetic stochastic events, which can impact the long-term survival of the population. Therefore, small populations are often considered at risk of endangerment or extinction, and are often of conservation concern.

<span class="mw-page-title-main">Neutral theory of molecular evolution</span> Theory of evolution by changes at the molecular level

The neutral theory of molecular evolution holds that most evolutionary changes occur at the molecular level, and most of the variation within and between species are due to random genetic drift of mutant alleles that are selectively neutral. The theory applies only for evolution at the molecular level, and is compatible with phenotypic evolution being shaped by natural selection as postulated by Charles Darwin.

Fitness is a quantitative representation of individual reproductive success. It is also equal to the average contribution to the gene pool of the next generation, made by the same individuals of the specified genotype or phenotype. Fitness can be defined either with respect to a genotype or to a phenotype in a given environment or time. The fitness of a genotype is manifested through its phenotype, which is also affected by the developmental environment. The fitness of a given phenotype can also be different in different selective environments.

Population genetics is a subfield of genetics that deals with genetic differences within and among populations, and is a part of evolutionary biology. Studies in this branch of biology examine such phenomena as adaptation, speciation, and population structure.

Allele frequency, or gene frequency, is the relative frequency of an allele at a particular locus in a population, expressed as a fraction or percentage. Specifically, it is the fraction of all chromosomes in the population that carry that allele over the total population or sample size. Microevolution is the change in allele frequencies that occurs over time within a population.

In evolutionary genetics, Muller's ratchet is a process which, in the absence of recombination, results in an accumulation of irreversible deleterious mutations. This happens because in the absence of recombination, and assuming reverse mutations are rare, offspring bear at least as much mutational load as their parents. Muller proposed this mechanism as one reason why sexual reproduction may be favored over asexual reproduction, as sexual organisms benefit from recombination and consequent elimination of deleterious mutations. The negative effect of accumulating irreversible deleterious mutations may not be prevalent in organisms which, while they reproduce asexually, also undergo other forms of recombination. This effect has also been observed in those regions of the genomes of sexual organisms that do not undergo recombination.

The effective population size (N_e) is size of an idealised population would experience the same rate of genetic drift or increase in inbreeding as in the real population. Idealised populations are based on unrealistic but convenient assumptions including random mating, simultaneous birth of each new generation, constant population size. For most quantities of interest and most real populations, N_e is smaller than the census population size N of a real population. The same population may have multiple effective population sizes for different properties of interest, including genetic drift and inbreeding.

Genetic load is the difference between the fitness of an average genotype in a population and the fitness of some reference genotype, which may be either the best present in a population, or may be the theoretically optimal genotype. The average individual taken from a population with a low genetic load will generally, when grown in the same conditions, have more surviving offspring than the average individual from a population with a high genetic load. Genetic load can also be seen as reduced fitness at the population level compared to what the population would have if all individuals had the reference high-fitness genotype. High genetic load may put a population in danger of extinction.

Mutation–selection balance is an equilibrium in the number of deleterious alleles in a population that occurs when the rate at which deleterious alleles are created by mutation equals the rate at which deleterious alleles are eliminated by selection. The majority of genetic mutations are neutral or deleterious; beneficial mutations are relatively rare. The resulting influx of deleterious mutations into a population over time is counteracted by negative selection, which acts to purge deleterious mutations. Setting aside other factors, the equilibrium number of deleterious alleles is then determined by a balance between the deleterious mutation rate and the rate at which selection purges those mutations.

Genetic distance is a measure of the genetic divergence between species or between populations within a species, whether the distance measures time from common ancestor or degree of differentiation. Populations with many similar alleles have small genetic distances. This indicates that they are closely related and have a recent common ancestor.

Genetic hitchhiking, also called genetic draft or the hitchhiking effect, is when an allele changes frequency not because it itself is under natural selection, but because it is near another gene that is undergoing a selective sweep and that is on the same DNA chain. When one gene goes through a selective sweep, any other nearby polymorphisms that are in linkage disequilibrium will tend to change their allele frequencies too. Selective sweeps happen when newly appeared mutations are advantageous and increase in frequency. Neutral or even slightly deleterious alleles that happen to be close by on the chromosome 'hitchhike' along with the sweep. In contrast, effects on a neutral locus due to linkage disequilibrium with newly appeared deleterious mutations are called background selection. Both genetic hitchhiking and background selection are stochastic (random) evolutionary forces, like genetic drift.

Neutral mutations are changes in DNA sequence that are neither beneficial nor detrimental to the ability of an organism to survive and reproduce. In population genetics, mutations in which natural selection does not affect the spread of the mutation in a species are termed neutral mutations. Neutral mutations that are inheritable and not linked to any genes under selection will be lost or will replace all other alleles of the gene. That loss or fixation of the gene proceeds based on random sampling known as genetic drift. A neutral mutation that is in linkage disequilibrium with other alleles that are under selection may proceed to loss or fixation via genetic hitchhiking and/or background selection.

Background selection describes the loss of genetic diversity at a locus due to negative selection against deleterious alleles with which it is in linkage disequilibrium. The name emphasizes the fact that the genetic background, or genomic environment, of a mutation has a significant impact on whether it will be preserved versus lost from a population. Background selection contradicts the assumption of the neutral theory of molecular evolution that the fixation or loss of a neutral allele can be described by one-locus models of genetic drift, independently from other loci. As well as reducing neutral nucleotide diversity, background selection reduces the fixation probability of beneficial mutations, and increases the fixation probability of deleterious mutations.

The nearly neutral theory of molecular evolution is a modification of the neutral theory of molecular evolution that accounts for the fact that not all mutations are either so deleterious such that they can be ignored, or else neutral. Slightly deleterious mutations are reliably purged only when their selection coefficient are greater than one divided by the effective population size. In larger populations, a higher proportion of mutations exceed this threshold for which genetic drift cannot overpower selection, leading to fewer fixation events and so slower molecular evolution.

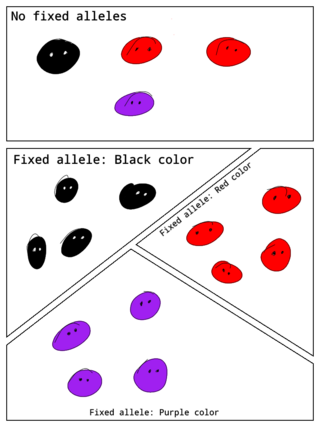
In population genetics, a fixed allele is an allele that is the only variant that exists for that gene in a population. A fixed allele is homozygous for all members of the population. The process by which alleles become fixed is called fixation.

The McDonald–Kreitman test is a statistical test often used by evolutionary and population biologists to detect and measure the amount of adaptive evolution within a species by determining whether adaptive evolution has occurred, and the proportion of substitutions that resulted from positive selection. To do this, the McDonald–Kreitman test compares the amount of variation within a species (polymorphism) to the divergence between species (substitutions) at two types of sites, neutral and nonneutral. A substitution refers to a nucleotide that is fixed within one species, but a different nucleotide is fixed within a second species at the same base pair of homologous DNA sequences. A site is nonneutral if it is either advantageous or deleterious. The two types of sites can be either synonymous or nonsynonymous within a protein-coding region. In a protein-coding sequence of DNA, a site is synonymous if a point mutation at that site would not change the amino acid, also known as a silent mutation. Because the mutation did not result in a change in the amino acid that was originally coded for by the protein-coding sequence, the phenotype, or the observable trait, of the organism is generally unchanged by the silent mutation. A site in a protein-coding sequence of DNA is nonsynonymous if a point mutation at that site results in a change in the amino acid, resulting in a change in the organism's phenotype. Typically, silent mutations in protein-coding regions are used as the "control" in the McDonald–Kreitman test.

Genetic purging is the increased pressure of natural selection against deleterious alleles prompted by inbreeding.

In population genetics, the allele frequency spectrum, sometimes called the site frequency spectrum, is the distribution of the allele frequencies of a given set of loci in a population or sample. Because an allele frequency spectrum is often a summary of or compared to sequenced samples of the whole population, it is a histogram with size depending on the number of sequenced individual chromosomes. Each entry in the frequency spectrum records the total number of loci with the corresponding derived allele frequency. Loci contributing to the frequency spectrum are assumed to be independently changing in frequency. Furthermore, loci are assumed to be biallelic, although extensions for multiallelic frequency spectra exist.

Allele age is the amount of time elapsed since an allele first appeared due to mutation. Estimating the time at which a certain allele appeared allows researchers to infer patterns of human migration, disease, and natural selection. Allele age can be estimated based on (1) the frequency of the allele in a population and (2) the genetic variation that occurs within different copies of the allele, also known as intra-allelic variation. While either of these methods can be used to estimate allele age, the use of both increases the accuracy of the estimation and can sometimes offer additional information regarding the presence of selection.

References

1 2 Arie Zackay (2007). Random Genetic Drift & Gene Fixation (PDF). Archived from the original (PDF) on 2016-03-04. Retrieved 2013-08-29.
1 2 Kimura, Motoo; Ohta, Tomoko (26 July 1968). "The average number of generations until fixation of a mutant gene in a finite population". Genetics. 61 (3): 763–771. doi:10.1093/genetics/61.3.763. PMC 1212239 . PMID 17248440.
↑ Kimura, Motoo (1983). The Neutral Theory of Molecular Evolution. The Edinburgh Building, Cambridge: Cambridge University Press. ISBN 978-0-521-23109-1 . Retrieved 16 November 2014.
1 2 Kimura, Motoo (29 January 1962). "On the probability of fixation of mutant genes in a population". Genetics. 47 (6): 713–719. doi:10.1093/genetics/47.6.713. PMC 1210364 . PMID 14456043.
↑ David H.A. Fitch (1997). Deviations from the null hypotheses: Finite populations sizes and genetic drift, mutation and gene flow.
↑ Otto, Sarah; Whitlock, Michael (7 March 1997). "The probability of fixation in populations of changing size" (PDF). Genetics. 146 (2): 723–733. doi:10.1093/genetics/146.2.723. PMC 1208011 . PMID 9178020 . Retrieved 14 September 2014.
↑ Caballero, Armando (9 March 1994). "Developments in the prediction of effective population size". Heredity. 73 (6): 657–679. doi: 10.1038/hdy.1994.174 . PMID 7814264.
↑ Griffiths, RC; Tavare, Simon (1998). "The Age of a Mutation in a General Coalescent Tree". Communications in Statistics. Stochastic Models. 14 (1&2): 273–295. doi:10.1080/15326349808807471.
↑ Walsh, Bruce (22 March 2001). "Estimating the Time to the Most Recent Common Ancestor for the Y chromosome or Mitochondrial DNA for a Pair of Individuals". Genetics. 158 (2): 897–912. doi:10.1093/genetics/158.2.897. PMC 1461668 . PMID 11404350.
↑ Schwartz, Drew (1969). "An Example of Gene Fixation Resulting from Selective Advantage in Suboptimal Conditions". The American Naturalist. 103 (933): 479–481. doi:10.1086/282615. JSTOR 2459409. S2CID 85366302.
↑ Rice, William (12 February 1987). "Genetic Hitchhiking and the Evolution of Reduced Genetic Activity of the Y Sex Chromosome". Genetics. 116 (1): 161–167. doi:10.1093/genetics/116.1.161. PMC 1203114 . PMID 3596229.
↑ Lee, Yuh; Langley, Charles; Begun, David (2014). "Differential Strengths of Positive Selection Revealed by Hitchhiking Effects at Small Physical Scales in Drosophila melanogaster". Molecular Biology and Evolution. 31 (4): 804–816. doi:10.1093/molbev/mst270. PMC 4043186 . PMID 24361994 . Retrieved 16 November 2014.