In mathematical analysis, the Dirac delta function, also known as the unit impulse, is a generalized function on the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one. Thus it can be represented heuristically as
In the calculus of variations and classical mechanics, the Euler–Lagrange equations are a system of second-order ordinary differential equations whose solutions are stationary points of the given action functional. The equations were discovered in the 1750s by Swiss mathematician Leonhard Euler and Italian mathematician Joseph-Louis Lagrange.

The path integral formulation is a description in quantum mechanics that generalizes the stationary action principle of classical mechanics. It replaces the classical notion of a single, unique classical trajectory for a system with a sum, or functional integral, over an infinity of quantum-mechanically possible trajectories to compute a quantum amplitude.
In mathematics and its applications, a Sturm–Liouville problem is a second-order linear ordinary differential equation of the form for given functions , and , together with some boundary conditions at extreme values of . The goals of a given Sturm–Liouville problem are:
In mathematical statistics, the Kullback–Leibler (KL) divergence, denoted , is a type of statistical distance: a measure of how much a model probability distribution Q is different from a true probability distribution P. Mathematically, it is defined as

In applied mechanics, bending characterizes the behavior of a slender structural element subjected to an external load applied perpendicularly to a longitudinal axis of the element.

In probability theory and statistics, the continuous uniform distributions or rectangular distributions are a family of symmetric probability distributions. Such a distribution describes an experiment where there is an arbitrary outcome that lies between certain bounds. The bounds are defined by the parameters, and which are the minimum and maximum values. The interval can either be closed or open. Therefore, the distribution is often abbreviated where stands for uniform distribution. The difference between the bounds defines the interval length; all intervals of the same length on the distribution's support are equally probable. It is the maximum entropy probability distribution for a random variable under no constraint other than that it is contained in the distribution's support.

Euler–Bernoulli beam theory is a simplification of the linear theory of elasticity which provides a means of calculating the load-carrying and deflection characteristics of beams. It covers the case corresponding to small deflections of a beam that is subjected to lateral loads only. By ignoring the effects of shear deformation and rotatory inertia, it is thus a special case of Timoshenko–Ehrenfest beam theory. It was first enunciated circa 1750, but was not applied on a large scale until the development of the Eiffel Tower and the Ferris wheel in the late 19th century. Following these successful demonstrations, it quickly became a cornerstone of engineering and an enabler of the Second Industrial Revolution.

Contact mechanics is the study of the deformation of solids that touch each other at one or more points. A central distinction in contact mechanics is between stresses acting perpendicular to the contacting bodies' surfaces and frictional stresses acting tangentially between the surfaces. Normal contact mechanics or frictionless contact mechanics focuses on normal stresses caused by applied normal forces and by the adhesion present on surfaces in close contact, even if they are clean and dry. Frictional contact mechanics emphasizes the effect of friction forces.
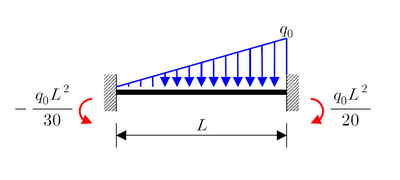
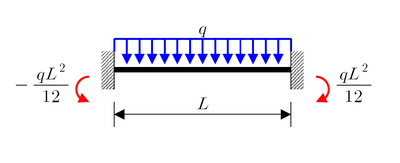
Macaulay's method (the double integration method) is a technique used in structural analysis to determine the deflection of Euler-Bernoulli beams. Use of Macaulay's technique is very convenient for cases of discontinuous and/or discrete loading. Typically partial uniformly distributed loads (u.d.l.) and uniformly varying loads (u.v.l.) over the span and a number of concentrated loads are conveniently handled using this technique.
The moment distribution method is a structural analysis method for statically indeterminate beams and frames developed by Hardy Cross. It was published in 1930 in an ASCE journal. The method only accounts for flexural effects and ignores axial and shear effects. From the 1930s until computers began to be widely used in the design and analysis of structures, the moment distribution method was the most widely practiced method.
The slope deflection method is a structural analysis method for beams and frames introduced in 1914 by George A. Maney. The slope deflection method was widely used for more than a decade until the moment distribution method was developed. In the book, "The Theory and Practice of Modern Framed Structures", written by J.B Johnson, C.W. Bryan and F.E. Turneaure, it is stated that this method was first developed "by Professor Otto Mohr in Germany, and later developed independently by Professor G.A. Maney". According to this book, professor Otto Mohr introduced this method for the first time in his book, "Evaluation of Trusses with Rigid Node Connections" or "Die Berechnung der Fachwerke mit Starren Knotenverbindungen".

The Timoshenko–Ehrenfest beam theory was developed by Stephen Timoshenko and Paul Ehrenfest early in the 20th century. The model takes into account shear deformation and rotational bending effects, making it suitable for describing the behaviour of thick beams, sandwich composite beams, or beams subject to high-frequency excitation when the wavelength approaches the thickness of the beam. The resulting equation is of 4th order but, unlike Euler–Bernoulli beam theory, there is also a second-order partial derivative present. Physically, taking into account the added mechanisms of deformation effectively lowers the stiffness of the beam, while the result is a larger deflection under a static load and lower predicted eigenfrequencies for a given set of boundary conditions. The latter effect is more noticeable for higher frequencies as the wavelength becomes shorter, and thus the distance between opposing shear forces decreases.

Direct integration is a structural analysis method for measuring internal shear, internal moment, rotation, and deflection of a beam.

In structural engineering, deflection is the degree to which a part of a long structural element is deformed laterally under a load. It may be quantified in terms of an angle or a distance . A longitudinal deformation is called elongation.

Sandwich theory describes the behaviour of a beam, plate, or shell which consists of three layers—two facesheets and one core. The most commonly used sandwich theory is linear and is an extension of first-order beam theory. The linear sandwich theory is of importance for the design and analysis of sandwich panels, which are of use in building construction, vehicle construction, airplane construction and refrigeration engineering.
In information theory and statistics, Kullback's inequality is a lower bound on the Kullback–Leibler divergence expressed in terms of the large deviations rate function. If P and Q are probability distributions on the real line, such that P is absolutely continuous with respect to Q, i.e. P << Q, and whose first moments exist, then where is the rate function, i.e. the convex conjugate of the cumulant-generating function, of , and is the first moment of

Structural engineering depends upon a detailed knowledge of loads, physics and materials to understand and predict how structures support and resist self-weight and imposed loads. To apply the knowledge successfully structural engineers will need a detailed knowledge of mathematics and of relevant empirical and theoretical design codes. They will also need to know about the corrosion resistance of the materials and structures, especially when those structures are exposed to the external environment.
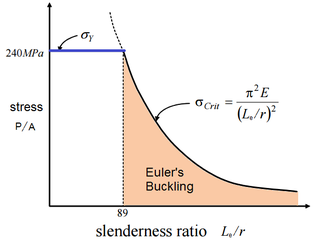
Euler's critical load or Euler's buckling load is the compressive load at which a slender column will suddenly bend or buckle. It is given by the formula:
A column can buckle due to its own weight with no other direct forces acting on it, in a failure mode called self-buckling. In conventional column buckling problems, the self-weight is often neglected since it is assumed to be small when compared to the applied axial loads. However, when this assumption is not valid, it is important to take the self-buckling into account.