In mathematics, specifically set theory, the continuum hypothesis is a hypothesis about the possible sizes of infinite sets. It states:
There is no set whose cardinality is strictly between that of the integers and the real numbers.
In mathematics, especially in order theory, the cofinality cf(A) of a partially ordered set A is the least of the cardinalities of the cofinal subsets of A.
In mathematics, an Erdős cardinal, also called a partition cardinal is a certain kind of large cardinal number introduced by Paul Erdős and András Hajnal.
The von Neumann cardinal assignment is a cardinal assignment that uses ordinal numbers. For a well-orderable set U, we define its cardinal number to be the smallest ordinal number equinumerous to U, using the von Neumann definition of an ordinal number. More precisely:
In mathematics, limit cardinals are certain cardinal numbers. A cardinal number λ is a weak limit cardinal if λ is neither a successor cardinal nor zero. This means that one cannot "reach" λ from another cardinal by repeated successor operations. These cardinals are sometimes called simply "limit cardinals" when the context is clear.
In set theory, a regular cardinal is a cardinal number that is equal to its own cofinality. More explicitly, this means that is a regular cardinal if and only if every unbounded subset has cardinality . Infinite well-ordered cardinals that are not regular are called singular cardinals. Finite cardinal numbers are typically not called regular or singular.
PCF theory is the name of a mathematical theory, introduced by Saharon Shelah, that deals with the cofinality of the ultraproducts of ordered sets. It gives strong upper bounds on the cardinalities of power sets of singular cardinals, and has many more applications as well. The abbreviation "PCF" stands for "possible cofinalities".
In mathematics, set-theoretic topology is a subject that combines set theory and general topology. It focuses on topological questions that can be solved using set-theoretic methods, for example, Suslin's problem.
In model theory, a branch of mathematical logic, the spectrum of a theory is given by the number of isomorphism classes of models in various cardinalities. More precisely, for any complete theory T in a language we write I(T, κ) for the number of models of T (up to isomorphism) of cardinality κ. The spectrum problem is to describe the possible behaviors of I(T, κ) as a function of κ. It has been almost completely solved for the case of a countable theory T.

James Earl Baumgartner was an American mathematician who worked in set theory, mathematical logic and foundations, and topology.
In the mathematical field of set theory, the proper forcing axiom (PFA) is a significant strengthening of Martin's axiom, where forcings with the countable chain condition (ccc) are replaced by proper forcings.
In mathematics, infinitary combinatorics, or combinatorial set theory, is an extension of ideas in combinatorics to infinite sets. Some of the things studied include continuous graphs and trees, extensions of Ramsey's theorem, and Martin's axiom. Recent developments concern combinatorics of the continuum and combinatorics on successors of singular cardinals.

Menachem Magidor is an Israeli mathematician who specializes in mathematical logic, in particular set theory. He served as president of the Hebrew University of Jerusalem, was president of the Association for Symbolic Logic from 1996 to 1998 and as president of the Division for Logic, Methodology and Philosophy of Science and Technology of the International Union for History and Philosophy of Science (DLMPST/IUHPS) from 2016 to 2019. In 2016 he was elected an honorary foreign member of the American Academy of Arts and Sciences. In 2018 he received the Solomon Bublick Award.
András Hajnal was a professor of mathematics at Rutgers University and a member of the Hungarian Academy of Sciences known for his work in set theory and combinatorics.
In the mathematical theory of infinite graphs, the Erdős–Dushnik–Miller theorem is a form of Ramsey's theorem stating that every infinite graph contains either a countably infinite independent set, or a clique with the same cardinality as the whole graph.
In mathematics, ψ0(Ωω), widely known as Buchholz's ordinal, is a large countable ordinal that is used to measure the proof-theoretic strength of some mathematical systems. In particular, it is the proof theoretic ordinal of the subsystem -CA0 of second-order arithmetic; this is one of the "big five" subsystems studied in reverse mathematics (Simpson 1999). It is also the proof-theoretic ordinal of , the theory of finitely iterated inductive definitions, and of , a fragment of Kripke-Platek set theory extended by an axiom stating every set is contained in an admissible set. Buchholz's ordinal is also the order type of the segment bounded by in Buchholz's ordinal notation . Lastly, it can be expressed as the limit of the sequence: , , , ...
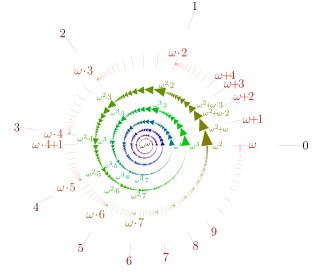
In set theory, an ordinal number, or ordinal, is a generalization of ordinal numerals aimed to extend enumeration to infinite sets.
In model theory, a discipline within mathematical logic, an abstract elementary class, or AEC for short, is a class of models with a partial order similar to the relation of an elementary substructure of an elementary class in first-order model theory. They were introduced by Saharon Shelah.
In the mathematical discipline of set theory, a cardinal characteristic of the continuum is an infinite cardinal number that may consistently lie strictly between , and the cardinality of the continuum, that is, the cardinality of the set of all real numbers. The latter cardinal is denoted or . A variety of such cardinal characteristics arise naturally, and much work has been done in determining what relations between them are provable, and constructing models of set theory for various consistent configurations of them.








