In engineering, a transfer function of an electronic or control system component is a mathematical function which theoretically models the device's output for each possible input. In its simplest form, this function is a two-dimensional graph of an independent scalar input versus the dependent scalar output, called a transfer curve or characteristic curve. Transfer functions for components are used to design and analyze systems assembled from components, particularly using the block diagram technique, in electronics and control theory.
In signal processing, group delay is the time delay of the amplitude envelopes of the various sinusoidal components of a signal through a device under test, and is a function of frequency for each component. Phase delay, in contrast, is the time delay of the phase as opposed to the time delay of the amplitude envelope.

The power spectrum of a time series describes the distribution of power into frequency components composing that signal. According to Fourier analysis, any physical signal can be decomposed into a number of discrete frequencies, or a spectrum of frequencies over a continuous range. The statistical average of a certain signal or sort of signal as analyzed in terms of its frequency content, is called its spectrum.
Fourier optics is the study of classical optics using Fourier transforms (FTs), in which the waveform being considered is regarded as made up of a combination, or superposition, of plane waves. It has some parallels to the Huygens–Fresnel principle, in which the wavefront is regarded as being made up of a combination of spherical wavefronts whose sum is the wavefront being studied. A key difference is that Fourier optics considers the plane waves to be natural modes of the propagation medium, as opposed to Huygens–Fresnel, where the spherical waves originate in the physical medium.

A normal mode of an oscillating system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The free motion described by the normal modes takes place at the fixed frequencies. These fixed frequencies of the normal modes of a system are known as its natural frequencies or resonant frequencies. A physical object, such as a building, bridge, or molecule, has a set of normal modes and their natural frequencies that depend on its structure, materials and boundary conditions. When relating to music, normal modes of vibrating instruments are called "harmonics" or "overtones".

Synthetic-aperture radar (SAR) is a form of radar that is used to create two-dimensional images or three-dimensional reconstructions of objects, such as landscapes. SAR uses the motion of the radar antenna over a target region to provide finer spatial resolution than conventional beam-scanning radars. SAR is typically mounted on a moving platform, such as an aircraft or spacecraft, and has its origins in an advanced form of side looking airborne radar (SLAR). The distance the SAR device travels over a target in the time taken for the radar pulses to return to the antenna creates the large synthetic antenna aperture. Typically, the larger the aperture, the higher the image resolution will be, regardless of whether the aperture is physical or synthetic – this allows SAR to create high-resolution images with comparatively small physical antennas. Additionally, SAR has the property of having larger apertures for more distant objects, allowing consistent spatial resolution over a range of viewing distances.

A sensor array is a group of sensors, usually deployed in a certain geometry pattern, used for collecting and processing electromagnetic or acoustic signals. The advantage of using a sensor array over using a single sensor lies in the fact that an array adds new dimensions to the observation, helping to estimate more parameters and improve the estimation performance. For example an array of radio antenna elements used for beamforming can increase antenna gain in the direction of the signal while decreasing the gain in other directions, i.e., increasing signal-to-noise ratio (SNR) by amplifying the signal coherently. Another example of sensor array application is to estimate the direction of arrival of impinging electromagnetic waves. The related processing method is called array signal processing. Application examples of array signal processing include radar/sonar, wireless communications, seismology, machine condition monitoring, astronomical observations fault diagnosis, etc.
In optics, an ultrashort pulse of light is an electromagnetic pulse whose time duration is of the order of a picosecond or less. Such pulses have a broadband optical spectrum, and can be created by mode-locked oscillators. They are commonly referred to as ultrafast events. Amplification of ultrashort pulses almost always requires the technique of chirped pulse amplification, in order to avoid damage to the gain medium of the amplifier.
In systems theory, a realization of a state space model is an implementation of a given input-output behavior. That is, given an input-output relationship, a realization is a quadruple of (time-varying) matrices such that
In statistical signal processing, the goal of spectral density estimation (SDE) is to estimate the spectral density of a random signal from a sequence of time samples of the signal. Intuitively speaking, the spectral density characterizes the frequency content of the signal. One purpose of estimating the spectral density is to detect any periodicities in the data, by observing peaks at the frequencies corresponding to these periodicities.
Least-squares spectral analysis (LSSA) is a method of estimating a frequency spectrum, based on a least squares fit of sinusoids to data samples, similar to Fourier analysis. Fourier analysis, the most used spectral method in science, generally boosts long-periodic noise in long gapped records; LSSA mitigates such problems.
Dynamic mode decomposition (DMD) is a dimensionality reduction algorithm developed by Peter Schmid in 2008. Given a time series of data, DMD computes a set of modes each of which is associated with a fixed oscillation frequency and decay/growth rate. For linear systems in particular, these modes and frequencies are analogous to the normal modes of the system, but more generally, they are approximations of the modes and eigenvalues of the composition operator. Due to the intrinsic temporal behaviors associated with each mode, DMD differs from dimensionality reduction methods such as principal component analysis, which computes orthogonal modes that lack predetermined temporal behaviors. Because its modes are not orthogonal, DMD-based representations can be less parsimonious than those generated by PCA. However, they can also be more physically meaningful because each mode is associated with a damped sinusoidal behavior in time.
The Eigensystem realization algorithm (ERA) is a system identification technique popular in civil engineering, in particular in structural health monitoring. ERA can be used as a modal analysis technique and generates a system realization using the time domain response (multi-)input and (multi-)output data. The ERA was proposed by Juang and Pappa and has been used for system identification of aerospace structures such as the Galileo spacecraft, turbines, civil structures and many other type of systems.
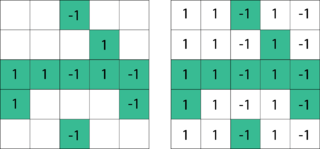
Matrix completion is the task of filling in the missing entries of a partially observed matrix. A wide range of datasets are naturally organized in matrix form. One example is the movie-ratings matrix, as appears in the Netflix problem: Given a ratings matrix in which each entry represents the rating of movie by customer if customer has watched movie and is otherwise missing, we would like to predict the remaining entries in order to make good recommendations to customers on what to watch next. Another example is the term-document matrix: The frequencies of words used in a collection of documents can be represented as a matrix, where each entry corresponds to the number of times the associated term appears in the indicated document.
The Dryden wind turbulence model, also known as Dryden gusts, is a mathematical model of continuous gusts accepted for use by the United States Department of Defense in certain aircraft design and simulation applications. The Dryden model treats the linear and angular velocity components of continuous gusts as spatially varying stochastic processes and specifies each component's power spectral density. The Dryden wind turbulence model is characterized by rational power spectral densities, so exact filters can be designed that take white noise inputs and output stochastic processes with the Dryden gusts' power spectral densities.
The von Kármán wind turbulence model is a mathematical model of continuous gusts. It matches observed continuous gusts better than that Dryden Wind Turbulence Model and is the preferred model of the United States Department of Defense in most aircraft design and simulation applications. The von Kármán model treats the linear and angular velocity components of continuous gusts as spatially varying stochastic processes and specifies each component's power spectral density. The von Kármán wind turbulence model is characterized by irrational power spectral densities, so filters can be designed that take white noise inputs and output stochastic processes with the approximated von Kármán gusts' power spectral densities.
The Sandia method is a method for generating a turbulent wind profile that can be used in aero-elastic software to evaluate the fatigue imparted on a turbine in a turbulent environment. That is, it generates time series of wind speeds at a set of points on a surface, say the plane of the rotor of a wind turbine. Analysis is performed initially in the frequency domain, where turbulence can be described quantitatively with more ease than the time domain. Then, the time series are obtained by inverse fast Fourier transforms.
In the field of statistical learning theory, matrix regularization generalizes notions of vector regularization to cases where the object to be learned is a matrix. The purpose of regularization is to enforce conditions, for example sparsity or smoothness, that can produce stable predictive functions. For example, in the more common vector framework, Tikhonov regularization optimizes over
Dynamic Substructuring (DS) is an engineering tool used to model and analyse the dynamics of mechanical systems by means of its components or substructures. Using the dynamic substructuring approach one is able to analyse the dynamic behaviour of substructures separately and to later on calculate the assembled dynamics using coupling procedures. Dynamic substructuring has several advantages over the analysis of the fully assembled system:












