In the mathematical field of algebraic topology, the fundamental group of a topological space is the group of the equivalence classes under homotopy of the loops contained in the space. It records information about the basic shape, or holes, of the topological space. The fundamental group is the first and simplest homotopy group. The fundamental group is a homotopy invariant—topological spaces that are homotopy equivalent have isomorphic fundamental groups.
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space. Intuitively, homotopy groups record information about the basic shape, or holes, of a topological space.
In mathematics, the Hurewicz theorem is a basic result of algebraic topology, connecting homotopy theory with homology theory via a map known as the Hurewicz homomorphism. The theorem is named after Witold Hurewicz, and generalizes earlier results of Henri Poincaré.
In mathematics, complex cobordism is a generalized cohomology theory related to cobordism of manifolds. Its spectrum is denoted by MU. It is an exceptionally powerful cohomology theory, but can be quite hard to compute, so often instead of using it directly one uses some slightly weaker theories derived from it, such as Brown–Peterson cohomology or Morava K-theory, that are easier to compute.
In algebraic topology, a branch of mathematics, a spectrum is an object representing a generalized cohomology theory. There are several different categories of spectra, but they all determine the same homotopy category, known as the stable homotopy category.
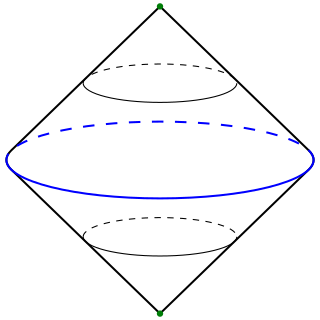
In topology, the suspension of a topological space X is intuitively obtained by stretching X into a cylinder and then collapsing both end faces to points. One views X as "suspended" between these end points.
In topology, a branch of mathematics, the loop space ΩX of a pointed topological space X is the space of (based) loops in X, i.e. continuous pointed maps from the pointed circle S1 to X, equipped with the compact-open topology. Two loops can be multiplied by concatenation. With this operation, the loop space is an A∞-space. That is, the multiplication is homotopy-coherently associative.
In mathematics, stable homotopy theory is that part of homotopy theory concerned with all structure and phenomena that remain after sufficiently many applications of the suspension functor. A founding result was the Freudenthal suspension theorem, which states that given any pointed space , the homotopy groups stabilize for sufficiently large. In particular, the homotopy groups of spheres stabilize for . For example,
In mathematics, the Whitehead product is a graded quasi-Lie algebra structure on the homotopy groups of a space. It was defined by J. H. C. Whitehead in.
In mathematics, the Puppe sequence is a construction of homotopy theory, so named after Dieter Puppe. It comes in two forms: a long exact sequence, built from the mapping fibre, and a long coexact sequence, built from the mapping cone. Intuitively, the Puppe sequence allows us to think of homology theory as a functor that takes spaces to long-exact sequences of groups. It is also useful as a tool to build long exact sequences of relative homotopy groups.
In the mathematical branch of algebraic topology, specifically homotopy theory, n-connectedness generalizes the concepts of path-connectedness and simple connectedness. To say that a space is n-connected is to say that its first n homotopy groups are trivial, and to say that a map is n-connected means that it is an isomorphism "up to dimension n, in homotopy".
In mathematics, the EHP spectral sequence is a spectral sequence used for inductively calculating the homotopy groups of spheres localized at some prime p. It is described in more detail in Ravenel and Mahowald (2001). It is related to the EHP long exact sequence of Whitehead (1953); the name "EHP" comes from the fact that George W. Whitehead named 3 of the maps of his sequence "E", "H", and "P".
In mathematics and specifically in topology, rational homotopy theory is a simplified version of homotopy theory for topological spaces, in which all torsion in the homotopy groups is ignored. It was founded by Dennis Sullivan (1977) and Daniel Quillen (1969). This simplification of homotopy theory makes calculations much easier.
In the mathematical disciplines of algebraic topology and homotopy theory, Eckmann–Hilton duality in its most basic form, consists of taking a given diagram for a particular concept and reversing the direction of all arrows, much as in category theory with the idea of the opposite category. A significantly deeper form argues that the fact that the dual notion of a limit is a colimit allows us to change the Eilenberg–Steenrod axioms for homology to give axioms for cohomology. It is named after Beno Eckmann and Peter Hilton.
In homotopy theory, a branch of mathematics, the Barratt–Priddy theorem expresses a connection between the homology of the symmetric groups and mapping spaces of spheres. The theorem is also often stated as a relation between the sphere spectrum and the classifying spaces of the symmetric groups via Quillen's plus construction.
In algebraic topology, the homotopy excision theorem offers a substitute for the absence of excision in homotopy theory. More precisely, let be an excisive triad with nonempty, and suppose the pair is ()-connected, , and the pair is -connected, . Then the map induced by the inclusion ,
In algebra, Quillen's Q-construction associates to an exact category an algebraic K-theory. More precisely, given an exact category C, the construction creates a topological space so that is the Grothendieck group of C and, when C is the category of finitely generated projective modules over a ring R, for , is the i-th K-group of R in the classical sense. One puts
This is a glossary of properties and concepts in algebraic topology in mathematics.
The Whitehead product is a mathematical construction introduced in Whitehead (1941). It has been a useful tool in determining the properties of spaces. The mathematical notion of space includes every shape that exists in our 3-dimensional world such as curves, surfaces, and solid figures. Since spaces are often presented by formulas, it is usually not possible to visually determine their geometric properties. Some of these properties are connectedness, the number of holes the space has, the knottedness of the space, and so on. Spaces are then studied by assigning algebraic constructions to them. This is similar to what is done in high school analytic geometry whereby to certain curves in the plane are assigned equations. The most common algebraic constructions are groups. These are sets such that any two members of the set can be combined to yield a third member of the set. In homotopy theory, one assigns a group to each space X and positive integer p called the pth homotopy group of X. These groups have been studied extensively and give information about the properties of the space X. There are then operations among these groups which provide additional information about the spaces. This has been very important in the study of homotopy groups.
In mathematics, homotopy theory is a systematic study of situations in which maps come with homotopies between them. It originated as a topic in algebraic topology but nowadays it is studied as an independent discipline. Besides algebraic topology, the theory has also been in used in other areas of mathematics such as algebraic geometry and category theory.























