In category theory, a branch of mathematics, a Grothendieck topology is a structure on a category C that makes the objects of C act like the open sets of a topological space. A category together with a choice of Grothendieck topology is called a site.
In category theory, a category is Cartesian closed if, roughly speaking, any morphism defined on a product of two objects can be naturally identified with a morphism defined on one of the factors. These categories are particularly important in mathematical logic and the theory of programming, in that their internal language is the simply typed lambda calculus. They are generalized by closed monoidal categories, whose internal language, linear type systems, are suitable for both quantum and classical computation.
In algebraic topology, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups Intuitively, singular homology counts, for each dimension n, the n-dimensional holes of a space. Singular homology is a particular example of a homology theory, which has now grown to be a rather broad collection of theories. Of the various theories, it is perhaps one of the simpler ones to understand, being built on fairly concrete constructions.
In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous, and the identity function is continuous. The study of Top and of properties of topological spaces using the techniques of category theory is known as categorical topology.
In category theory, a branch of mathematics, a pushout is the colimit of a diagram consisting of two morphisms f : Z → X and g : Z → Y with a common domain. The pushout consists of an object P along with two morphisms X → P and Y → P that complete a commutative square with the two given morphisms f and g. In fact, the defining universal property of the pushout essentially says that the pushout is the "most general" way to complete this commutative square. Common notations for the pushout are and .

In topology, the wedge sum is a "one-point union" of a family of topological spaces. Specifically, if X and Y are pointed spaces the wedge sum of X and Y is the quotient space of the disjoint union of X and Y by the identification
In topology, a branch of mathematics, the smash product of two pointed spaces and is the quotient of the product space X × Y under the identifications (x, y0) ∼ (x0, y) for all x in X and y in Y. The smash product is itself a pointed space, with basepoint being the equivalence class of. The smash product is usually denoted X ∧ Y or X ⨳ Y. The smash product depends on the choice of basepoints.

In topology, especially algebraic topology, the coneof a topological space is the space defined as:
In mathematics, the derived categoryD(A) of an abelian category A is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on A. The construction proceeds on the basis that the objects of D(A) should be chain complexes in A, with two such chain complexes considered isomorphic when there is a chain map that induces an isomorphism on the level of homology of the chain complexes. Derived functors can then be defined for chain complexes, refining the concept of hypercohomology. The definitions lead to a significant simplification of formulas otherwise described by complicated spectral sequences.
In general topology and related areas of mathematics, the initial topology on a set , with respect to a family of functions on , is the coarsest topology on X that makes those functions continuous.
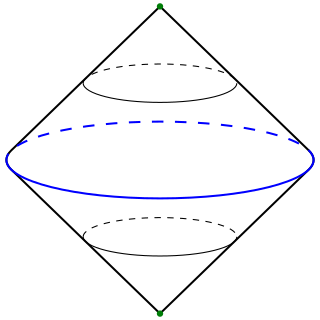
In topology, a branch of mathematics, the suspension of a topological space X is intuitively obtained by stretching X into a cylinder and then collapsing both end faces to points. One views X as "suspended" between these end points.
In mathematics, in particular homotopy theory, a continuous mapping
In mathematics, especially homotopy theory, the mapping cone is a construction of topology, analogous to a quotient space. It is also called the homotopy cofiber, and also notated . Its dual, a fibration, is called the mapping fibre. The mapping cone can be understood to be a mapping cylinder , with one end of the cylinder collapsed to a point. Thus, mapping cones are frequently applied in the homotopy theory of pointed spaces.
In general topology and related areas of mathematics, the final topology on a set with respect to a family of functions from topological spaces into is the finest topology on that makes all those functions continuous.
In mathematics, the homotopy category is a category built from the category of topological spaces which in a sense identifies two spaces that have the same shape. The phrase is in fact used for two different categories, as discussed below.
In topology, a branch of mathematics, the loop space ΩX of a pointed topological space X is the space of (based) loops in X, i.e. continuous pointed maps from the pointed circle S1 to X, equipped with the compact-open topology. Two loops can be multiplied by concatenation. With this operation, the loop space is an A∞-space. That is, the multiplication is homotopy-coherently associative.
In mathematics, the category of manifolds, often denoted Manp, is the category whose objects are manifolds of smoothness class Cp and whose morphisms are p-times continuously differentiable maps. This is a category because the composition of two Cp maps is again continuous and of class Cp.
In mathematics, especially in the area of topology known as algebraic topology, an induced homomorphism is a homomorphism derived in a canonical way from another map. For example, a continuous map from a topological space X to a space Y induces a group homomorphism from the fundamental group of X to the fundamental group of Y.
In mathematics, more specifically algebraic topology, a pair is shorthand for an inclusion of topological spaces . Sometimes is assumed to be a cofibration. A morphism from to is given by two maps and such that .
In mathematics, homotopy theory is a systematic study of situations in which maps come with homotopies between them. It originated as a topic in algebraic topology but nowadays is studied as an independent discipline. Besides algebraic topology, the theory has also been used in other areas of mathematics such as algebraic geometry (e.g., A1 homotopy theory) and category theory (specifically the study of higher categories).



























