In mathematics, a series is, roughly speaking, a description of the operation of adding infinitely many quantities, one after the other, to a given starting quantity. The study of series is a major part of calculus and its generalization, mathematical analysis. Series are used in most areas of mathematics, even for studying finite structures through generating functions. In addition to their ubiquity in mathematics, infinite series are also widely used in other quantitative disciplines such as physics, computer science, statistics and finance.

In mathematics, the concept of a measure is a generalization and formalization of geometrical measures and other common notions, such as mass and probability of events. These seemingly distinct concepts have many similarities and can often be treated together in a single mathematical context. Measures are foundational in probability theory, integration theory, and can be generalized to assume negative values, as with electrical charge. Far-reaching generalizations of measure are widely used in quantum physics and physics in general.
In mathematical analysis, a null set is a measurable set that has measure zero. This can be characterized as a set that can be covered by a countable union of intervals of arbitrarily small total length.
In mathematics, the branch of real analysis studies the behavior of real numbers, sequences and series of real numbers, and real functions. Some particular properties of real-valued sequences and functions that real analysis studies include convergence, limits, continuity, smoothness, differentiability and integrability.
In the mathematical field of analysis, uniform convergence is a mode of convergence of functions stronger than pointwise convergence. A sequence of functions converges uniformly to a limiting function on a set if, given any arbitrarily small positive number , a number can be found such that each of the functions differs from by no more than at every pointin. Described in an informal way, if converges to uniformly, then the rate at which approaches is "uniform" throughout its domain in the following sense: in order to guarantee that falls within a certain distance of , we do not need to know the value of in question — there can be found a single value of independent of , such that choosing will ensure that is within of for all . In contrast, pointwise convergence of to merely guarantees that for any given in advance, we can find so that, for that particular, falls within of whenever .

In calculus, Taylor's theorem gives an approximation of a k-times differentiable function around a given point by a polynomial of degree k, called the kth-order Taylor polynomial. For a smooth function, the Taylor polynomial is the truncation at the order k of the Taylor series of the function. The first-order Taylor polynomial is the linear approximation of the function, and the second-order Taylor polynomial is often referred to as the quadratic approximation. There are several versions of Taylor's theorem, some giving explicit estimates of the approximation error of the function by its Taylor polynomial.
Distributions, also known as Schwartz distributions or generalized functions, are objects that generalize the classical notion of functions in mathematical analysis. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative.
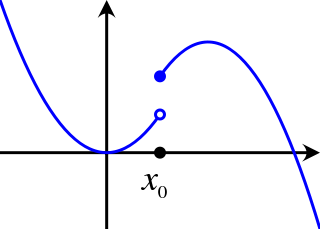
In mathematical analysis, semicontinuity is a property of extended real-valued functions that is weaker than continuity. An extended real-valued function is uppersemicontinuous at a point if, roughly speaking, the function values for arguments near are not much higher than

In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions. Functions of each type are infinitely differentiable, but complex analytic functions exhibit properties that do not generally hold for real analytic functions. A function is analytic if and only if its Taylor series about x0 converges to the function in some neighborhood for every x0 in its domain.
In mathematics, an infinite series of numbers is said to converge absolutely if the sum of the absolute values of the summands is finite. More precisely, a real or complex series is said to converge absolutely if for some real number Similarly, an improper integral of a function, is said to converge absolutely if the integral of the absolute value of the integrand is finite—that is, if
In the mathematical field of real analysis, the monotone convergence theorem is any of a number of related theorems proving the convergence of monotonic sequences that are also bounded. Informally, the theorems state that if a sequence is increasing and bounded above by a supremum, then the sequence will converge to the supremum; in the same way, if a sequence is decreasing and is bounded below by an infimum, it will converge to the infimum.
In functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces. All Banach and Hilbert spaces are Fréchet spaces. Spaces of infinitely differentiable functions are typical examples of Fréchet spaces, many of which are typically not Banach spaces.
In mathematical analysis Fubini's theorem is a result that gives conditions under which it is possible to compute a double integral by using an iterated integral, introduced by Guido Fubini in 1907. One may switch the order of integration if the double integral yields a finite answer when the integrand is replaced by its absolute value.
In mathematics, smooth functions and analytic functions are two very important types of functions. One can easily prove that any analytic function of a real argument is smooth. The converse is not true, as demonstrated with the counterexample below.
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function together with its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, i.e. a Banach space. Intuitively, a Sobolev space is a space of functions possessing sufficiently many derivatives for some application domain, such as partial differential equations, and equipped with a norm that measures both the size and regularity of a function.
In Fourier analysis, a multiplier operator is a type of linear operator, or transformation of functions. These operators act on a function by altering its Fourier transform. Specifically they multiply the Fourier transform of a function by a specified function known as the multiplier or symbol. Occasionally, the term multiplier operator itself is shortened simply to multiplier. In simple terms, the multiplier reshapes the frequencies involved in any function. This class of operators turns out to be broad: general theory shows that a translation-invariant operator on a group which obeys some regularity conditions can be expressed as a multiplier operator, and conversely. Many familiar operators, such as translations and differentiation, are multiplier operators, although there are many more complicated examples such as the Hilbert transform.

In mathematical analysis, the smoothness of a function is a property measured by the number of continuous derivatives it has over some domain, called differentiability class. At the very minimum, a function could be considered smooth if it is differentiable everywhere. At the other end, it might also possess derivatives of all orders in its domain, in which case it is said to be infinitely differentiable and referred to as a C-infinity function.

In mathematics, the integral of a non-negative function of a single variable can be regarded, in the simplest case, as the area between the graph of that function and the x-axis. The Lebesgue integral, named after French mathematician Henri Lebesgue, extends the integral to a larger class of functions. It also extends the domains on which these functions can be defined.
In mathematics, a limit is the value that a function approaches as the input approaches some value. Limits are essential to calculus and mathematical analysis, and are used to define continuity, derivatives, and integrals.
In the mathematical discipline of functional analysis, a differentiable vector-valued function from Euclidean space is a differentiable function valued in a topological vector space (TVS) whose domains is a subset of some finite-dimensional Euclidean space. It is possible to generalize the notion of derivative to functions whose domain and codomain are subsets of arbitrary topological vector spaces (TVSs) in multiple ways. But when the domain of a TVS-valued function is a subset of a finite-dimensional Euclidean space then many of these notions become logically equivalent resulting in a much more limited number of generalizations of the derivative and additionally, differentiability is also more well-behaved compared to the general case. This article presents the theory of -times continuously differentiable functions on an open subset of Euclidean space , which is an important special case of differentiation between arbitrary TVSs. This importance stems partially from the fact that every finite-dimensional vector subspace of a Hausdorff topological vector space is TVS isomorphic to Euclidean space so that, for example, this special case can be applied to any function whose domain is an arbitrary Hausdorff TVS by restricting it to finite-dimensional vector subspaces.











