Fugit

Last updated
Calculation of fugit:

For Fugit — where n is the number of time-steps in the tree; t is the time to option expiry; and i is the current time-step — the calculation is as follows: [1] ; see also [2]

(1) set the fugit of all nodes at the end of the tree equal to i = n

(2) work backwards recursively:

  • if the option should be exercised at a node, set the fugit at that node equal to its period
  • if the option should not exercised at a node, set the fugit to the risk-neutral expected fugit over the next period.

(3) the number calculated in this fashion at the beginning of the first period (i=0) is the current fugit.

Finally, to annualize the fugit, multiply the resulting value by t / n.

In mathematical finance, fugit is the expected (or optimal) date to exercise an American- or Bermudan option. It is useful for hedging purposes here; see Greeks (finance) and Optimal stopping#Option trading. The term was first introduced by Mark Garman in an article "Semper tempus fugit" published in 1989. [3] The Latin term "tempus fugit" means "time flies" [4] and Garman suggested the name because "time flies especially when you're having fun managing your book of American options".

Details

Fugit provides an estimate of when an option would be exercised, which is then a useful indication for the maturity to use when hedging American or Bermudan products with European options. [2] Fugit is thus used for the hedging of convertible bonds, equity linked convertible notes, and any putable or callable exotic coupon notes. Although see [5] and [6] for qualifications here. Fugit is also useful in estimating "the (risk-neutral) expected life of the option" [7] for Employee stock options (note the brackets).

Fugit is calculated as "the expected time to exercise of American options", [3] and is also described as the "risk-neutral expected life of the option" [1] The computation requires a binomial tree — although a Finite difference approach would also apply [2] — where, a second quantity, additional to option price, is required at each node of the tree; [8] see methodology aside. Note that fugit is not always a unique value. [5]

Nassim Taleb proposes a "rho fudge", as a “shortcut method... to find the right duration (i.e., expected time to termination) for an American option”. [9] Taleb terms this result “Omega” as opposed to fugit. The formula is

Omega = Nominal Duration x (Rho2 of an American option / Rho2 of a European option).

Here, Rho2 refers to sensitivity to dividends or the foreign interest rate, as opposed to the more usual rho which measures sensitivity to (local) interest rates; the latter is sometimes used, however. [10] Taleb notes that this approach was widely applied, already in the 1980s, preceding Garman. [11]

Related Research Articles

Financial economics is the branch of economics characterized by a "concentration on monetary activities", in which "money of one type or another is likely to appear on both sides of a trade". Its concern is thus the interrelation of financial variables, such as prices, interest rates and shares, as opposed to those concerning the real economy. It has two main areas of focus: asset pricing and corporate finance; the first being the perspective of providers of capital, i.e. investors, and the second of users of capital.

The Black–Scholes or Black–Scholes–Merton model is a mathematical model for the dynamics of a financial market containing derivative investment instruments. From the partial differential equation in the model, known as the Black–Scholes equation, one can deduce the Black–Scholes formula, which gives a theoretical estimate of the price of European-style options and shows that the option has a unique price regardless of the risk of the security and its expected return. The formula led to a boom in options trading and provided mathematical legitimacy to the activities of the Chicago Board Options Exchange and other options markets around the world. It is widely used, although often with some adjustments, by options market participants.

Value at risk risk measure on a specific portfolio of financial assets

Value at risk (VaR) is a measure of the risk of loss for investments. It estimates how much a set of investments might lose, given normal market conditions, in a set time period such as a day. VaR is typically used by firms and regulators in the financial industry to gauge the amount of assets needed to cover possible losses.

In finance, the style or family of an option is the class into which the option falls, usually defined by the dates on which the option may be exercised. The vast majority of options are either European or American (style) options. These options—as well as others where the payoff is calculated similarly—are referred to as "vanilla options". Options where the payoff is calculated differently are categorized as "exotic options". Exotic options can pose challenging problems in valuation and hedging.

In finance, the binomial options pricing model (BOPM) provides a generalizable numerical method for the valuation of options. Essentially, the model uses a "discrete-time" model of the varying price over time of the underlying financial instrument, addressing cases where the closed-form Black–Scholes formula is wanting.

In mathematical finance, the Greeks are the quantities representing the sensitivity of the price of derivatives such as options to a change in underlying parameters on which the value of an instrument or portfolio of financial instruments is dependent. The name is used because the most common of these sensitivities are denoted by Greek letters. Collectively these have also been called the risk sensitivities, risk measures or hedge parameters.

A swaption is an option granting its owner the right but not the obligation to enter into an underlying swap. Although options can be traded on a variety of swaps, the term "swaption" typically refers to options on interest rate swaps.

In finance, an exotic option is an option which has features making it more complex than commonly traded vanilla options. Like the more general exotic derivatives they may have several triggers relating to determination of payoff. An exotic option may also include non-standard underlying instrument, developed for a particular client or for a particular market. Exotic options are more complex than options that trade on an exchange, and are generally traded over the counter (OTC).

Rational pricing is the assumption in financial economics that asset prices will reflect the arbitrage-free price of the asset as any deviation from this price will be "arbitraged away". This assumption is useful in pricing fixed income securities, particularly bonds, and is fundamental to the pricing of derivative instruments.

Nassim Nicholas Taleb French-Lebanese-American essayist, scholar, statistician, former trader and risk analyst

Nassim Nicholas Taleb is a Lebanese-American essayist, scholar, statistician, and former option trader and risk analyst, whose work concerns problems of randomness, probability, and uncertainty. His 2007 book The Black Swan has been described by The Sunday Times as one of the twelve most influential books since World War II.

In finance, a bond option is an option to buy or sell a bond at a certain price on or before the option expiry date. These instruments are typically traded OTC.

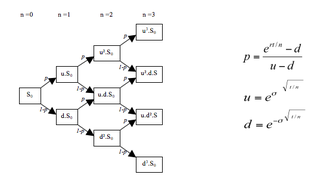
Lattice model (finance) method for evaluating stock options that divides time into discrete intervals

In finance, a lattice model is a technique applied to the valuation of derivatives, where a discrete time model is required. For equity options, a typical example would be pricing an American option, where a decision as to option exercise is required at "all" times before and including maturity. A continuous model, on the other hand, such as Black–Scholes, would only allow for the valuation of European options, where exercise is on the option's maturity date. For interest rate derivatives lattices are additionally useful in that they address many of the issues encountered with continuous models, such as pull to par. The method is also used for valuing certain exotic options, where because of path dependence in the payoff, Monte Carlo methods for option pricing fail to account for optimal decisions to terminate the derivative by early exercise., though methods now exist for solving this problem.

The black swan theory or theory of black swan events is a metaphor that describes an event that comes as a surprise, has a major effect, and is often inappropriately rationalized after the fact with the benefit of hindsight. The term is based on an ancient saying that presumed black swans did not exist – a saying that became reinterpreted to teach a different lesson after black swans were discovered in the wild.

Option (finance) Right to buy or sell a certain thing at a later date at an agreed price

In finance, an option is a contract which gives the buyer the right, but not the obligation, to buy or sell an underlying asset or instrument at a specified strike price prior to or on a specified date, depending on the form of the option. The strike price may be set by reference to the spot price of the underlying security or commodity on the day an option is taken out, or it may be fixed at a discount or at a premium. The seller has the corresponding obligation to fulfill the transaction – to sell or buy – if the buyer (owner) "exercises" the option. An option that conveys to the owner the right to buy at a specific price is referred to as a call; an option that conveys the right of the owner to sell at a specific price is referred to as a put. Both are commonly traded, but the call option is more frequently discussed.

Rainbow option is a derivative exposed to two or more sources of uncertainty, as opposed to a simple option that is exposed to one source of uncertainty, such as the price of underlying asset.

A basket option is a financial derivative, more specifically an exotic option, whose underlying is a weighted sum or average of different assets that have been grouped together in a basket. For example, an index option, where a number of stocks have been grouped together in an index and the option is based on the price of the index.

Taleb distribution probability distribution with a positive mean and a left fat tail; with expected small positive payoff and a small chance of serious losses

In economics and finance, a Taleb distribution is the statistical profile of an investment which normally provides a payoff of small positive returns, while carrying a small but significant risk of catastrophic losses. The term was coined by journalist Martin Wolf and economist John Kay to describe investments with a "high probability of a modest gain and a low probability of huge losses in any period."

In finance, model risk is the risk of loss resulting from using insufficiently accurate models to make decisions, originally and frequently in the context of valuing financial securities. However, model risk is more and more prevalent in activities other than financial securities valuation, such as assigning consumer credit scores, real-time probability prediction of fraudulent credit card transactions, and computing the probability of air flight passenger being a terrorist. Rebonato in 2002 defines model risk as "the risk of occurrence of a significant difference between the mark-to-model value of a complex and/or illiquid instrument, and the price at which the same instrument is revealed to have traded in the market".

Mathematical finance, also known as quantitative finance and financial mathematics, is a field of applied mathematics, concerned with mathematical modeling of financial markets. Generally, mathematical finance will derive and extend the mathematical or numerical models without necessarily establishing a link to financial theory, taking observed market prices as input. Mathematical consistency is required, not compatibility with economic theory. Thus, for example, while a financial economist might study the structural reasons why a company may have a certain share price, a financial mathematician may take the share price as a given, and attempt to use stochastic calculus to obtain the corresponding value of derivatives of the stock. The fundamental theorem of arbitrage-free pricing is one of the key theorems in mathematical finance, while the Black–Scholes equation and formula are amongst the key results.

In finance, a contingent claim is a derivative whose future payoff depends on the value of another “underlying” asset, or more generally, that is dependent on the realization of some uncertain future event. These are so named, since there is only a payoff under certain contingencies. Any derivative instrument that is not a contingent claim is called a forward commitment. The prototypical contingent claim is an option, the right to buy or sell the underlying asset at a specified exercise price by a certain expiration date; whereas (vanilla) swaps, forwards, and futures are forward commitments, since these grant no such optionality. Contingent claims are applied under financial economics in developing models and theory, and in corporate finance as a valuation framework.

References

  1. 1 2 Mark Rubinstein in an article "Guiding force"; the calculation is detailed on pages 43 and 44, as well as in Exotic Options Archived 2015-09-24 at the Wayback Machine , a working paper by the same author.
  2. 1 2 3 Eric Benhamou: Fugit (options)
  3. 1 2 Mark Garman in an article "Semper tempus fugit" published in 1989 by Risk Publications, and included in the book "From Black Scholes to Black Holes" pages 89-91
  4. ↑ "Tempus it et tamquam mobilis aura volat". Audio Latin Proverbs. Retrieved 30 July 2012.
  5. 1 2 Christopher Davenport, Citigroup, 2003. "Convertible Bonds A Guide".
  6. ↑ Paul Wilmott's comment on a wilmott.com forum Archived 2015-07-04 at the Wayback Machine : "But, yes, remember that you need to put the real drift in there otherwise it's just the risk-neutral time and therefore not so relevant."
  7. ↑ Mark Rubinstein (1995). "On the Accounting Valuation of Employee Stock Options Archived 2017-08-11 at the Wayback Machine ", Journal of Derivatives , Fall 1995
  8. ↑ Example VBA code
  9. ↑ Pg. 178 of Nassim Taleb (1997). Dynamic Hedging: Managing Vanilla and Exotic Options. New York: John Wiley & Sons. ISBN   0-471-15280-3.
  10. ↑ See for example this discussion on nuclearphynance.com.
  11. ↑ Nassim Taleb: Review of Derivatives by Mark Rubinstein
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.