
In geometry, two geometric objects are perpendicular if they intersect at right angles, i.e. at an angle of 90 degrees or π/2 radians. The condition of perpendicularity may be represented graphically using the perpendicular symbol, ⟂. Perpendicular intersections can happen between two lines, between a line and a plane, and between two planes.

In geometry, the nine-point circle is a circle that can be constructed for any given triangle. It is so named because it passes through nine significant concyclic points defined from the triangle. These nine points are:

The orthocenter of a triangle, usually denoted by H, is the point where the three altitudes intersect. The orthocenter lies inside the triangle if and only if the triangle is acute. For a right triangle, the orthocenter coincides with the vertex at the right angle.

In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches the three sides. The center of the incircle is a triangle center called the triangle's incenter.

In geometry, an orthocentric system is a set of four points on a plane, one of which is the orthocenter of the triangle formed by the other three. Equivalently, the lines passing through disjoint pairs among the points are perpendicular, and the four circles passing through any three of the four points have the same radius.

In geometry, the Euler line, named after Leonhard Euler, is a line determined from any triangle that is not equilateral. It is a central line of the triangle, and it passes through several important points determined from the triangle, including the orthocenter, the circumcenter, the centroid, the Exeter point and the center of the nine-point circle of the triangle.
In geometry, inversive geometry is the study of inversion, a transformation of the Euclidean plane that maps circles or lines to other circles or lines and that preserves the angles between crossing curves. Many difficult problems in geometry become much more tractable when an inversion is applied. Inversion seems to have been discovered by a number of people contemporaneously, including Steiner (1824), Quetelet (1825), Bellavitis (1836), Stubbs and Ingram (1842–3) and Kelvin (1845).

In geometry, the power center of three circles, also called the radical center, is the intersection point of the three radical axes of the pairs of circles. If the radical center lies outside of all three circles, then it is the center of the unique circle that intersects the three given circles orthogonally; the construction of this orthogonal circle corresponds to Monge's problem. This is a special case of the three conics theorem.
In projective geometry, duality or plane duality is a formalization of the striking symmetry of the roles played by points and lines in the definitions and theorems of projective planes. There are two approaches to the subject of duality, one through language and the other a more functional approach through special mappings. These are completely equivalent and either treatment has as its starting point the axiomatic version of the geometries under consideration. In the functional approach there is a map between related geometries that is called a duality. Such a map can be constructed in many ways. The concept of plane duality readily extends to space duality and beyond that to duality in any finite-dimensional projective geometry.

In geometry, Euler's rotation theorem states that, in three-dimensional space, any displacement of a rigid body such that a point on the rigid body remains fixed, is equivalent to a single rotation about some axis that runs through the fixed point. It also means that the composition of two rotations is also a rotation. Therefore the set of rotations has a group structure, known as a rotation group.

In Euclidean plane geometry, Apollonius's problem is to construct circles that are tangent to three given circles in a plane (Figure 1). Apollonius of Perga posed and solved this famous problem in his work Ἐπαφαί ; this work has been lost, but a 4th-century AD report of his results by Pappus of Alexandria has survived. Three given circles generically have eight different circles that are tangent to them (Figure 2), a pair of solutions for each way to divide the three given circles in two subsets.
In geometry, collinearity of a set of points is the property of their lying on a single line. A set of points with this property is said to be collinear. In greater generality, the term has been used for aligned objects, that is, things being "in a line" or "in a row".
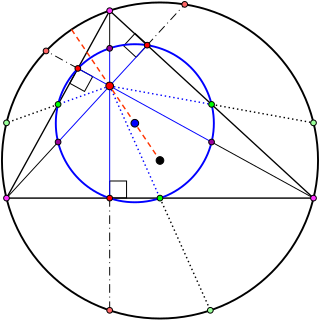
In geometry, the nine-point center is a triangle center, a point defined from a given triangle in a way that does not depend on the placement or scale of the triangle. It is so called because it is the center of the nine-point circle, a circle that passes through nine significant points of the triangle: the midpoints of the three edges, the feet of the three altitudes, and the points halfway between the orthocenter and each of the three vertices. The nine-point center is listed as point X(5) in Clark Kimberling's Encyclopedia of Triangle Centers.
Geometry is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. Geometry is one of the oldest mathematical sciences.

In geometry, a set of Johnson circles comprises three circles of equal radius r sharing one common point of intersection H. In such a configuration the circles usually have a total of four intersections : the common point H that they all share, and for each of the three pairs of circles one more intersection point. If any two of the circles happen to osculate, they only have H as a common point, and it will then be considered that H be their 2-wise intersection as well; if they should coincide we declare their 2-wise intersection be the point diametrically opposite H. The three 2-wise intersection points define the reference triangle of the figure. The concept is named after Roger Arthur Johnson.

In geometry, the de Longchamps point of a triangle is a triangle center named after French mathematician Gaston Albert Gohierre de Longchamps. It is the reflection of the orthocenter of the triangle about the circumcenter.
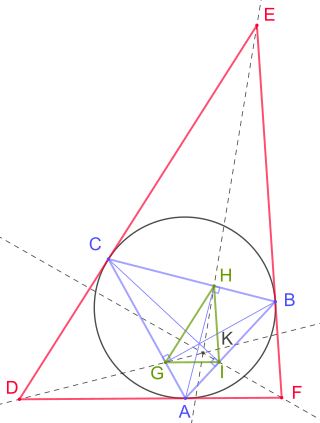
In geometry, the tangential triangle of a reference triangle is the triangle whose sides are on the tangent lines to the reference triangle's circumcircle at the reference triangle's vertices. Thus the incircle of the tangential triangle coincides with the circumcircle of the reference triangle.

The Soddy line of a triangle is the line that goes through the centers of the two Soddy circles of that triangle.
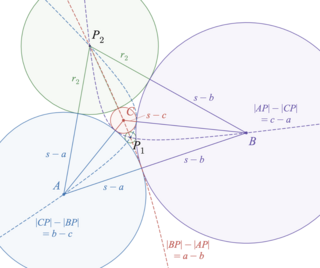
In geometry, the Soddy circles of a triangle are two circles associated with any triangle in the plane. Their centers are the Soddy centers of the triangle. They are all named for Frederick Soddy, who rediscovered Descartes' theorem on the radii of mutually tangent quadruples of circles.
















