
A colloid is a mixture in which one substance consisting of microscopically dispersed insoluble particles is suspended throughout another substance. Some definitions specify that the particles must be dispersed in a liquid, while others extend the definition to include substances like aerosols and gels. The term colloidal suspension refers unambiguously to the overall mixture. A colloid has a dispersed phase and a continuous phase. The dispersed phase particles have a diameter of approximately 1 nanometre to 1 micrometre.

In physics, chemistry, and thermodynamics, an equation of state is a thermodynamic equation relating state variables, which describe the state of matter under a given set of physical conditions, such as pressure, volume, temperature, or internal energy. Most modern equations of state are formulated in the Helmholtz free energy. Equations of state are useful in describing the properties of pure substances and mixtures in liquids, gases, and solid states as well as the state of matter in the interior of stars.

Fick's laws of diffusion describe diffusion and were first posited by Adolf Fick in 1855 on the basis of largely experimental results. They can be used to solve for the diffusion coefficient, D. Fick's first law can be used to derive his second law which in turn is identical to the diffusion equation.

A gel is a semi-solid that can have properties ranging from soft and weak to hard and tough. Gels are defined as a substantially dilute cross-linked system, which exhibits no flow when in the steady-state, although the liquid phase may still diffuse through this system. A gel has been defined phenomenologically as a soft, solid or solid-like material consisting of two or more components, one of which is a liquid, present in substantial quantity.
Electron density or electronic density is the measure of the probability of an electron being present at an infinitesimal element of space surrounding any given point. It is a scalar quantity depending upon three spatial variables and is typically denoted as either or . The density is determined, through definition, by the normalised -electron wavefunction which itself depends upon variables. Conversely, the density determines the wave function modulo up to a phase factor, providing the formal foundation of density functional theory.
Polymer chemistry is a sub-discipline of chemistry that focuses on the structures of chemicals, chemical synthesis, and chemical and physical properties of polymers and macromolecules. The principles and methods used within polymer chemistry are also applicable through a wide range of other chemistry sub-disciplines like organic chemistry, analytical chemistry, and physical chemistry. Many materials have polymeric structures, from fully inorganic metals and ceramics to DNA and other biological molecules. However, polymer chemistry is typically related to synthetic and organic compositions. Synthetic polymers are ubiquitous in commercial materials and products in everyday use, such as plastics, and rubbers, and are major components of composite materials. Polymer chemistry can also be included in the broader fields of polymer science or even nanotechnology, both of which can be described as encompassing polymer physics and polymer engineering.
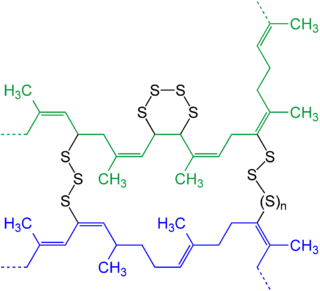
In chemistry and biology a cross-link is a bond or a short sequence of bonds that links one polymer chain to another. These links may take the form of covalent bonds or ionic bonds and the polymers can be either synthetic polymers or natural polymers.
The DLVO theory explains the aggregation and kinetic stability of aqueous dispersions quantitatively and describes the force between charged surfaces interacting through a liquid medium. It combines the effects of the van der Waals attraction and the electrostatic repulsion due to the so-called double layer of counterions. The electrostatic part of the DLVO interaction is computed in the mean field approximation in the limit of low surface potentials - that is when the potential energy of an elementary charge on the surface is much smaller than the thermal energy scale, . For two spheres of radius each having a charge separated by a center-to-center distance in a fluid of dielectric constant containing a concentration of monovalent ions, the electrostatic potential takes the form of a screened-Coulomb or Yukawa potential,
In materials science, the sol–gel process is a method for producing solid materials from small molecules. The method is used for the fabrication of metal oxides, especially the oxides of silicon (Si) and titanium (Ti). The process involves conversion of monomers into a colloidal solution (sol) that acts as the precursor for an integrated network of either discrete particles or network polymers. Typical precursors are metal alkoxides. Sol-gel process is used to produce ceramic nanoparticles.

Step-growth polymerization refers to a type of polymerization mechanism in which bi-functional or multifunctional monomers react to form first dimers, then trimers, longer oligomers and eventually long chain polymers. Many naturally occurring and some synthetic polymers are produced by step-growth polymerization, e.g. polyesters, polyamides, polyurethanes, etc. Due to the nature of the polymerization mechanism, a high extent of reaction is required to achieve high molecular weight. The easiest way to visualize the mechanism of a step-growth polymerization is a group of people reaching out to hold their hands to form a human chain—each person has two hands. There also is the possibility to have more than two reactive sites on a monomer: In this case branched polymers production take place.
The degree of polymerization, or DP, is the number of monomeric units in a macromolecule or polymer or oligomer molecule.
In step-growth polymerization, the Carothers equation gives the degree of polymerization, Xn, for a given fractional monomer conversion, p.
A polymer brush is the name given to a surface coating consisting of polymers tethered to a surface. The brush may be either in a solvated state, where the tethered polymer layer consists of polymer and solvent, or in a melt state, where the tethered chains completely fill up the space available. These polymer layers can be tethered to flat substrates such as silicon wafers, or highly curved substrates such as nanoparticles. Also, polymers can be tethered in high density to another single polymer chain, although this arrangement is normally named a bottle brush. Additionally, there is a separate class of polyelectrolyte brushes, when the polymer chains themselves carry an electrostatic charge.
Curing is a chemical process employed in polymer chemistry and process engineering that produces the toughening or hardening of a polymer material by cross-linking of polymer chains. Even if it is strongly associated with the production of thermosetting polymers, the term "curing" can be used for all the processes where a solid product is obtained from a liquid solution, such as with PVC plastisols.
In polymer chemistry, the gel point is an abrupt change in the viscosity of a solution containing polymerizable components. At the gel point, a solution undergoes gelation, as reflected in a loss in fluidity. Gelation is characteristic of polymerizations that include crosslinkers that can form 2- or 3-dimensional networks. For example, the condensation of a dicarboxylic acid and a triol will give rise to a gel whereas the same dicarboxylic acid and a diol will not. The gel is often a small percentage of the mixture, even though it greatly influences the properties of the bulk.
In computational chemistry, the Fukui function or frontier function is a function that describes the electron density in a frontier orbital, as a result of a small change in the total number of electrons. The condensed Fukui function or condensed reactivity indicator is the same idea, but applied to an atom within a molecule, rather than a point in three-dimensional space.
An organogel is a class of gel composed of a liquid organic phase within a three-dimensional, cross-linked network. Organogel networks can form in two ways. The first is classic gel network formation via polymerization. This mechanism converts a precursor solution of monomers with various reactive sites into polymeric chains that grow into a single covalently-linked network. At a critical concentration, the polymeric network becomes large enough so that on the macroscopic scale, the solution starts to exhibit gel-like physical properties: an extensive continuous solid network, no steady-state flow, and solid-like rheological properties. However, organogels that are “low molecular weight gelators” can also be designed to form gels via self-assembly. Secondary forces, such as van der Waals or hydrogen bonding, cause monomers to cluster into a non-covalently bonded network that retains organic solvent, and as the network grows, it exhibits gel-like physical properties. Both gelation mechanisms lead to gels characterized as organogels.

Star-shaped polymers are the simplest class of branched polymers with a general structure consisting of several linear chains connected to a central core. The core, or the center, of the polymer can be an atom, molecule, or macromolecule; the chains, or "arms", consist of variable-length organic chains. Star-shaped polymers in which the arms are all equivalent in length and structure are considered homogeneous, and ones with variable lengths and structures are considered heterogeneous.
Flory–Stockmayer theory is a theory governing the cross-linking and gelation of step-growth polymers. The Flory-Stockmayer theory represents an advancement from the Carothers equation, allowing for the identification of the gel point for polymer synthesis not at stoichiometric balance. The theory was initially conceptualized by Paul Flory in 1941 and then was further developed by Walter Stockmayer in 1944 to include cross-linking with an arbitrary initial size distribution. The Flory-Stockmayer theory was the first theory investigating percolation processes. Flory–Stockmayer theory is a special case of random graph theory of gelation.

Random graph theory of gelation is a mathematical theory for sol–gel processes. The theory is a collection of results that generalise the Flory–Stockmayer theory, and allow identification of the gel point, gel fraction, size distribution of polymers, molar mass distribution and other characteristics for a set of many polymerising monomers carrying arbitrary numbers and types of reactive functional groups.



























