
A CT scan, also known as computed tomography scan, and formerly known as a computerized axial tomography scan or CAT scan, makes use of computer-processed combinations of many X-ray measurements taken from different angles to produce cross-sectional (tomographic) images of specific areas of a scanned object, allowing the user to see inside the object without cutting.
An inverse problem in science is the process of calculating from a set of observations the causal factors that produced them: for example, calculating an image in X-ray computed tomography, source reconstruction in acoustics, or calculating the density of the Earth from measurements of its gravity field.

Iterative reconstruction refers to iterative algorithms used to reconstruct 2D and 3D images in certain imaging techniques. For example, in computed tomography an image must be reconstructed from projections of an object. Here, iterative reconstruction techniques are usually a better, but computationally more expensive alternative to the common filtered back projection (FBP) method, which directly calculates the image in a single reconstruction step. In recent research works, scientists have shown that extremely fast computations and massive parallelism is possible for iterative reconstruction, which makes iterative reconstruction practical for commercialization.

In geometry and science, a cross section is the non-empty intersection of a solid body in three-dimensional space with a plane, or the analog in higher-dimensional spaces. Cutting an object into slices creates many parallel cross sections. The boundary of a cross section in three-dimensional space that is parallel to two of the axes, that is, parallel to the plane determined by these axes, is a sometimes referred to as a contour line; for example, if a plane cuts through mountains of a raised-relief map parallel to the ground, the result is a contour line in two-dimensional space showing points on the surface of the mountains of equal elevation.
In mathematics, the projection-slice theorem, central slice theorem or Fourier slice theorem in two dimensions states that the results of the following two calculations are equal:
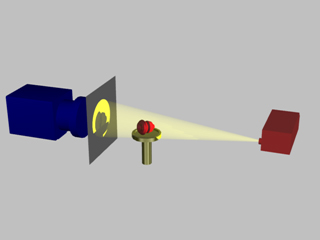
In microtomography X-ray scanners, cone beam reconstruction is one of two common scanning methods, the other being Fan beam reconstruction.
In mathematics, convex geometry is the branch of geometry studying convex sets, mainly in Euclidean space. Convex sets occur naturally in many areas: computational geometry, convex analysis, discrete geometry, functional analysis, geometry of numbers, integral geometry, linear programming, probability theory, game theory, etc.
In geometry, a vertex is a point where two or more curves, lines, or edges meet. As a consequence of this definition, the point where two lines meet to form an angle and the corners of polygons and polyhedra are vertices.

Tomosynthesis, also digital tomosynthesis (DTS), is a method for performing high-resolution limited-angle tomography at radiation dose levels comparable with projectional radiography. It has been studied for a variety of clinical applications, including vascular imaging, dental imaging, orthopedic imaging, mammographic imaging, musculoskeletal imaging, and chest imaging.
In computer vision and computer graphics, 3D reconstruction is the process of capturing the shape and appearance of real objects. This process can be accomplished either by active or passive methods. If the model is allowed to change its shape in time, this is referred to as non-rigid or spatio-temporal reconstruction.
In mathematics, the X-ray transform is an integral transform introduced by Fritz John in 1938 that is one of the cornerstones of modern integral geometry. It is very closely related to the Radon transform, and coincides with it in two dimensions. In higher dimensions, the X-ray transform of a function is defined by integrating over lines rather than over hyperplanes as in the Radon transform. The X-ray transform derives its name from X-ray tomography because the X-ray transform of a function ƒ represents the attenuation data of a tomographic scan through an inhomogeneous medium whose density is represented by the function ƒ. Inversion of the X-ray transform is therefore of practical importance because it allows one to reconstruct an unknown density ƒ from its known attenuation data.

Industrial computed tomography (CT) scanning is any computer-aided tomographic process, usually X-ray computed tomography, that uses irradiation to produce three-dimensional internal and external representations of a scanned object. Industrial CT scanning has been used in many areas of industry for internal inspection of components. Some of the key uses for industrial CT scanning have been flaw detection, failure analysis, metrology, assembly analysis and reverse engineering applications. Just as in medical imaging, industrial imaging includes both nontomographic radiography and computed tomographic radiography.
The Mojette Transform is an application of discrete geometry. More specifically, it is a discrete and exact version of the Radon transform, thus a projection operator.

In radiography, focal plane tomography is tomography by simultaneously moving the X-ray generator and X-ray detector so as to keep a consistent exposure of only the plane of interest during image acquisition. This was the main method of obtaining tomographs in medical imaging until the late-1970s. It has since been largely replaced by more advanced imaging techniques such as CT and MRI. It remains in use today in a few specialized applications, such as for acquiring orthopantomographs of the jaw in dental radiography.

X-ray computed tomography operates by using an X-ray generator that rotates around the object; X-ray detectors are positioned on the opposite side of the circle from the X-ray source.

The history of X-ray computed tomography goes back to at least 1917 with the mathematical theory of the Radon transform In October 1963, William H. Oldendorf received a U.S. patent for a "radiant energy apparatus for investigating selected areas of interior objects obscured by dense material". The first commercially viable CT scanner was invented by Sir Godfrey Hounsfield in 1967.














