Discrete tomography

Last updated
A discrete tomography reconstruction problem for two vertical and horizontal directions (left), together with its (non-unique) solution (right). The task is to color some of the white points black so that the number of black points in the rows and columns match the blue numbers. Discrete tomography.png
A discrete tomography reconstruction problem for two vertical and horizontal directions (left), together with its (non-unique) solution (right). The task is to color some of the white points black so that the number of black points in the rows and columns match the blue numbers.

Discrete tomography [1] [2] focuses on the problem of reconstruction of binary images (or finite subsets of the integer lattice) from a small number of their projections.

Contents

In general, tomography deals with the problem of determining shape and dimensional information of an object from a set of projections. From the mathematical point of view, the object corresponds to a function and the problem posed is to reconstruct this function from its integrals or sums over subsets of its domain. In general, the tomographic inversion problem may be continuous or discrete. In continuous tomography both the domain and the range of the function are continuous and line integrals are used. In discrete tomography the domain of the function may be either discrete or continuous, and the range of the function is a finite set of real, usually nonnegative numbers. In continuous tomography when a large number of projections is available, accurate reconstructions can be made by many different algorithms. It is typical for discrete tomography that only a few projections (line sums) are used. In this case, conventional techniques all fail. A special case of discrete tomography deals with the problem of the reconstruction of a binary image from a small number of projections. The name discrete tomography is due to Larry Shepp, who organized the first meeting devoted to this topic (DIMACS Mini-Symposium on Discrete Tomography, September 19, 1994, Rutgers University).

Theory

Discrete tomography has strong connections with other mathematical fields, such as number theory, [3] [4] [5] discrete mathematics, [6] [7] [8] computational complexity theory [9] [10] and combinatorics. [11] [12] [13] In fact, a number of discrete tomography problems were first discussed as combinatorial problems. In 1957, H. J. Ryser found a necessary and sufficient condition for a pair of vectors being the two orthogonal projections of a discrete set. In the proof of his theorem, Ryser also described a reconstruction algorithm, the very first reconstruction algorithm for a general discrete set from two orthogonal projections. In the same year, David Gale found the same consistency conditions, but in connection with the network flow problem. [14] Another result of Ryser's is the definition of the switching operation by which discrete sets having the same projections can be transformed into each other.

The problem of reconstructing a binary image from a small number of projections generally leads to a large number of solutions. It is desirable to limit the class of possible solutions to only those that are typical of the class of the images which contains the image being reconstructed by using a priori information, such as convexity or connectedness.

Theorems

For further results, see [1] [2]

Algorithms

Among the reconstruction methods one can find algebraic reconstruction techniques (e.g., DART [18] [19] or [20] ), greedy algorithms (see [21] for approximation guarantees), and Monte Carlo algorithms. [22] [23]

Applications

Various algorithms have been applied in image processing, [18] medicine, three-dimensional statistical data security problems, computer tomograph assisted engineering and design, electron microscopy [24] [25] and materials science, including the 3DXRD microscope. [22] [23] [26]

A form of discrete tomography also forms the basis of nonograms, a type of logic puzzle in which information about the rows and columns of a digital image is used to reconstruct the image. [27]

See also

Related Research Articles

An inverse problem in science is the process of calculating from a set of observations the causal factors that produced them: for example, calculating an image in X-ray computed tomography, source reconstruction in acoustics, or calculating the density of the Earth from measurements of its gravity field. It is called an inverse problem because it starts with the effects and then calculates the causes. It is the inverse of a forward problem, which starts with the causes and then calculates the effects.

<span class="mw-page-title-main">Geometry of numbers</span>

Geometry of numbers is the part of number theory which uses geometry for the study of algebraic numbers. Typically, a ring of algebraic integers is viewed as a lattice in and the study of these lattices provides fundamental information on algebraic numbers. The geometry of numbers was initiated by Hermann Minkowski.

<span class="mw-page-title-main">Tomography</span> Imaging by sections or sectioning using a penetrative wave

Tomography is imaging by sections or sectioning that uses any kind of penetrating wave. The method is used in radiology, archaeology, biology, atmospheric science, geophysics, oceanography, plasma physics, materials science, cosmochemistry, astrophysics, quantum information, and other areas of science. The word tomography is derived from Ancient Greek τόμος tomos, "slice, section" and γράφω graphō, "to write" or, in this context as well, "to describe." A device used in tomography is called a tomograph, while the image produced is a tomogram.

In computer science, 2-satisfiability, 2-SAT or just 2SAT is a computational problem of assigning values to variables, each of which has two possible values, in order to satisfy a system of constraints on pairs of variables. It is a special case of the general Boolean satisfiability problem, which can involve constraints on more than two variables, and of constraint satisfaction problems, which can allow more than two choices for the value of each variable. But in contrast to those more general problems, which are NP-complete, 2-satisfiability can be solved in polynomial time.

<span class="mw-page-title-main">Radon transform</span> Integral transform

In mathematics, the Radon transform is the integral transform which takes a function f defined on the plane to a function Rf defined on the (two-dimensional) space of lines in the plane, whose value at a particular line is equal to the line integral of the function over that line. The transform was introduced in 1917 by Johann Radon, who also provided a formula for the inverse transform. Radon further included formulas for the transform in three dimensions, in which the integral is taken over planes. It was later generalized to higher-dimensional Euclidean spaces and more broadly in the context of integral geometry. The complex analogue of the Radon transform is known as the Penrose transform. The Radon transform is widely applicable to tomography, the creation of an image from the projection data associated with cross-sectional scans of an object.

<span class="mw-page-title-main">Tomographic reconstruction</span> Estimate object properties from a finite number of projections

Tomographic reconstruction is a type of multidimensional inverse problem where the challenge is to yield an estimate of a specific system from a finite number of projections. The mathematical basis for tomographic imaging was laid down by Johann Radon. A notable example of applications is the reconstruction of computed tomography (CT) where cross-sectional images of patients are obtained in non-invasive manner. Recent developments have seen the Radon transform and its inverse used for tasks related to realistic object insertion required for testing and evaluating computed tomography use in airport security.

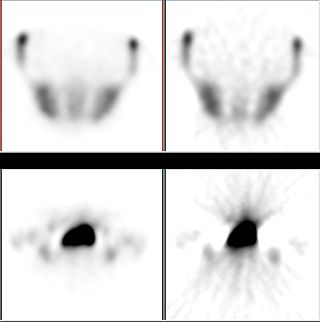
<span class="mw-page-title-main">Iterative reconstruction</span>

Iterative reconstruction refers to iterative algorithms used to reconstruct 2D and 3D images in certain imaging techniques. For example, in computed tomography an image must be reconstructed from projections of an object. Here, iterative reconstruction techniques are usually a better, but computationally more expensive alternative to the common filtered back projection (FBP) method, which directly calculates the image in a single reconstruction step. In recent research works, scientists have shown that extremely fast computations and massive parallelism is possible for iterative reconstruction, which makes iterative reconstruction practical for commercialization.

A logical matrix, binary matrix, relation matrix, Boolean matrix, or (0, 1)-matrix is a matrix with entries from the Boolean domain B = {0, 1}. Such a matrix can be used to represent a binary relation between a pair of finite sets. It is an important tool in combinatorial mathematics and theoretical computer science.

<span class="mw-page-title-main">Electron tomography</span>

Electron tomography (ET) is a tomography technique for obtaining detailed 3D structures of sub-cellular, macro-molecular, or materials specimens. Electron tomography is an extension of traditional transmission electron microscopy and uses a transmission electron microscope to collect the data. In the process, a beam of electrons is passed through the sample at incremental degrees of rotation around the center of the target sample. This information is collected and used to assemble a three-dimensional image of the target. For biological applications, the typical resolution of ET systems are in the 5–20 nm range, suitable for examining supra-molecular multi-protein structures, although not the secondary and tertiary structure of an individual protein or polypeptide. Recently, atomic resolution in 3D electron tomography reconstructions has been demonstrated.

Compressed sensing is a signal processing technique for efficiently acquiring and reconstructing a signal, by finding solutions to underdetermined linear systems. This is based on the principle that, through optimization, the sparsity of a signal can be exploited to recover it from far fewer samples than required by the Nyquist–Shannon sampling theorem. There are two conditions under which recovery is possible. The first one is sparsity, which requires the signal to be sparse in some domain. The second one is incoherence, which is applied through the isometric property, which is sufficient for sparse signals. Compressed sensing has applications in, for example, MRI where the incoherence condition is typically satisfied.

<span class="mw-page-title-main">Algebraic reconstruction technique</span> Technique in computed tomography

The algebraic reconstruction technique (ART) is an iterative reconstruction technique used in computed tomography. It reconstructs an image from a series of angular projections. Gordon, Bender and Herman first showed its use in image reconstruction; whereas the method is known as Kaczmarz method in numerical linear algebra.

Geometric tomography is a mathematical field that focuses on problems of reconstructing homogeneous objects from tomographic data. More precisely, according to R.J. Gardner, "Geometric tomography deals with the retrieval of information about a geometric object from data concerning its projections (shadows) on planes or cross-sections by planes."

<span class="mw-page-title-main">3D reconstruction from multiple images</span> Creation of a 3D model from a set of images

3D reconstruction from multiple images is the creation of three-dimensional models from a set of images. It is the reverse process of obtaining 2D images from 3D scenes.

In the mathematical fields of numerical analysis and approximation theory, box splines are piecewise polynomial functions of several variables. Box splines are considered as a multivariate generalization of basis splines (B-splines) and are generally used for multivariate approximation/interpolation. Geometrically, a box spline is the shadow (X-ray) of a hypercube projected down to a lower-dimensional space. Box splines and simplex splines are well studied special cases of polyhedral splines which are defined as shadows of general polytopes.

In iterative reconstruction in digital imaging, interior reconstruction (also known as limited field of view (LFV) reconstruction) is a technique to correct truncation artifacts caused by limiting image data to a small field of view. The reconstruction focuses on an area known as the region of interest (ROI). Although interior reconstruction can be applied to dental or cardiac CT images, the concept is not limited to CT. It is applied with one of several methods.

Simultaneous algebraic reconstruction technique (SART) is a computerized tomography (CT) imaging algorithm useful in cases when the projection data is limited; it was proposed by Anders Andersen and Avinash Kak in 1984. It generates a good reconstruction in just one iteration and it is superior to standard algebraic reconstruction technique (ART).

<span class="mw-page-title-main">Operation of computed tomography</span>

X-ray computed tomography operates by using an X-ray generator that rotates around the object; X-ray detectors are positioned on the opposite side of the circle from the X-ray source.

Photon-counting computed tomography (PCCT) is a form of X-ray computed tomography (CT) in which X-rays are detected using a photon-counting detector (PCD) which registers the interactions of individual photons. By keeping track of the deposited energy in each interaction, the detector pixels of a PCD each record an approximate energy spectrum, making it a spectral or energy-resolved CT technique. In contrast, more conventional CT scanners use energy-integrating detectors (EIDs), where the total energy deposited in a pixel during a fixed period of time is registered. These EIDs thus register only photon intensity, comparable to black-and-white photography, whereas PCDs register also spectral information, similar to color photography.

X-ray diffraction computed tomography is an experimental technique that combines X-ray diffraction with the computed tomography data acquisition approach. X-ray diffraction (XRD) computed tomography (CT) was first introduced in 1987 by Harding et al. using a laboratory diffractometer and a monochromatic X-ray pencil beam. The first implementation of the technique at synchrotron facilities was performed in 1998 by Kleuker et al.

References

  1. 1 2 Herman, G. T. and Kuba, A., Discrete Tomography: Foundations, Algorithms, and Applications, Birkhäuser Boston, 1999
  2. 1 2 Herman, G. T. and Kuba, A., Advances in Discrete Tomography and Its Applications, Birkhäuser Boston, 2007
  3. ↑ R.J. Gardner, P. Gritzmann, Discrete tomography: determination of finite sets by X-rays, Trans. Amer. Math. Soc. 349 (1997), no. 6, 2271-2295.
  4. ↑ L. Hajdu, R. Tijdeman, Algebraic aspects of discrete tomography, J. reine angew. Math. 534 (2001), 119-128.
  5. ↑ A. Alpers, R. Tijdeman, The Two-Dimensional Prouhet-Tarry-Escott Problem, Journal of Number Theory, 123 (2), pp. 403-412, 2007 .
  6. ↑ S. Brunetti, A. Del Lungo, P. Gritzmann, S. de Vries, On the reconstruction of binary and permutation matrices under (binary) tomographic constraints. Theoret. Comput. Sci. 406 (2008), no. 1-2, 63-71.
  7. ↑ A. Alpers, P. Gritzmann, On Stability, Error Correction, and Noise Compensation in Discrete Tomography, SIAM Journal on Discrete Mathematics 20 (1), pp. 227-239, 2006
  8. ↑ P. Gritzmann, B. Langfeld, On the index of Siegel grids and its application to the tomography of quasicrystals. European J. Combin. 29 (2008), no. 8, 1894-1909.
  9. 1 2 R.J. Gardner, P. Gritzmann, D. Prangenberg, On the computational complexity of reconstructing lattice sets from their X-rays. Discrete Math. 202 (1999), no. 1-3, 45-71.
  10. 1 2 C. Dürr, F. Guiñez, M. Matamala, Reconstructing 3-Colored Grids from Horizontal and Vertical Projections Is NP-hard. ESA 2009: 776-787.
  11. ↑ H.J. Ryser, Matrices of zeros and ones, Bull. Amer. Math. Soc. 66 1960 442-464.
  12. ↑ D. Gale, A theorem on flows in networks, Pacific J. Math. 7 (1957), 1073-1082.
  13. ↑ E. Barcucci, S. Brunetti, A. Del Lungo, M. Nivat, Reconstruction of lattice sets from their horizontal, vertical and diagonal X-rays, Discrete Mathematics 241(1-3): 65-78 (2001).
  14. ↑ Brualdi, Richard A. (2006). Combinatorial matrix classes. Encyclopedia of Mathematics and Its Applications. Vol. 108. Cambridge: Cambridge University Press. p.  27. ISBN   978-0-521-86565-4. Zbl   1106.05001.
  15. 1 2 A. Alpers, P. Gritzmann, L. Thorens, Stability and Instability in Discrete Tomography, Lecture Notes in Computer Science 2243; Digital and Image Geometry (Advanced Lectures), G. Bertrand, A. Imiya, R. Klette (Eds.), pp. 175-186, Springer-Verlag, 2001.
  16. ↑ A. Alpers, S. Brunetti, On the Stability of Reconstructing Lattice Sets from X-rays Along Two Directions, Lecture Notes in Computer Science 3429; Digital Geometry for Computer Imagery, E. Andres, G. Damiand, P. Lienhardt (Eds.), pp. 92-103, Springer-Verlag, 2005.
  17. ↑ B. van Dalen, Stability results for uniquely determined sets from two directions in discrete tomography, Discrete Mathematics 309(12): 3905-3916 (2009).
  18. 1 2 Batenburg, Joost; Sijbers, Jan - DART: A practical reconstruction algorithm for discrete tomography - In: IEEE transactions on image processing, Vol. 20, Nr. 9, p. 2542-2553, (2011). doi : 10.1109/TIP.2011.2131661
  19. ↑ W. van Aarle, K J. Batenburg, and J. Sijbers, Automatic parameter estimation for the Discrete Algebraic Reconstruction Technique (DART), IEEE Transactions on Image Processing, 2012
  20. ↑ K. J. Batenburg, and J. Sijbers, "Generic iterative subset algorithms for discrete tomography", Discrete Applied Mathematics, vol. 157, no. 3, pp. 438-451, 2009
  21. ↑ P. Gritzmann, S. de Vries, M. Wiegelmann, Approximating binary images from discrete X-rays, SIAM J. Optim. 11 (2000), no. 2, 522-546.
  22. 1 2 A. Alpers, H.F. Poulsen, E. Knudsen, G.T. Herman, A Discrete Tomography Algorithm for Improving the Quality of 3DXRD Grain Maps, Journal of Applied Crystallography 39, pp. 582-588, 2006 .
  23. 1 2 L. Rodek, H.F. Poulsen, E. Knudsen, G.T. Herman, A stochastic algorithm for reconstruction of grain maps of moderately deformed specimens based on X-ray diffraction, Journal of Applied Crystallography 40:313-321, 2007.
  24. ↑ S. Bals, K. J. Batenburg, J. Verbeeck, J. Sijbers, and G. Van Tendeloo, "Quantitative 3D reconstruction of catalyst particles for bamboo-like carbon-nanotubes", Nano Letters, Vol. 7, Nr. 12, p. 3669-3674, (2007) doi : 10.1021/nl071899m
  25. ↑ Batenburg J., S. Bals, Sijbers J., C. Kubel, P.A. Midgley, J.C. Hernandez, U. Kaiser, E.R. Encina, E.A. Coronado, and G. Van Tendeloo, "3D imaging of nanomaterials by discrete tomography", Ultramicroscopy, Vol. 109, p. 730-740, (2009) doi : 10.1016/j.ultramic.2009.01.009
  26. ↑ K. J. Batenburg, J. Sijbers, H. F. Poulsen, and E. Knudsen, "DART: A Robust Algorithm for Fast Reconstruction of 3D Grain Maps", Journal of Applied Crystallography, vol. 43, pp. 1464-1473, 2010
  27. ↑ Games Magazine Presents Paint by Numbers. Random House. 1994. ISBN   978-0-8129-2384-1.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.