Projection (mathematics)

Last updated May 31, 2024

In mathematics, a projection is an idempotent mapping of a set (or other mathematical structure) into a subset (or sub-structure). In this case, idempotent means that projecting twice is the same as projecting once. The restriction to a subspace of a projection is also called a projection, even if the idempotence property is lost. An everyday example of a projection is the casting of shadows onto a plane (sheet of paper): the projection of a point is its shadow on the sheet of paper, and the projection (shadow) of a point on the sheet of paper is that point itself (idempotency). The shadow of a three-dimensional sphere is a closed disk. Originally, the notion of projection was introduced in Euclidean geometry to denote the projection of the three-dimensional Euclidean space onto a plane in it, like the shadow example. The two main projections of this kind are:

The projection from a point onto a plane or central projection: If $C$ is a point, called the center of projection, then the projection of a point $P$ different from $C$ onto a plane that does not contain $C$ is the intersection of the line $CP$ with the plane. The points $P$ such that the line $CP$ is parallel to the plane does not have any image by the projection, but one often says that they project to a point at infinity of the plane (see Projective geometry for a formalization of this terminology). The projection of the point $C$ itself is not defined.
The projection parallel to a direction $D$ , onto a plane or parallel projection : The image of a point $P$ is the intersection of the plane with the line parallel to $D$ passing through $P$ . See Affine space § Projection for an accurate definition, generalized to any dimension.^{[ citation needed ]}

The concept of projection in mathematics is a very old one, and most likely has its roots in the phenomenon of the shadows cast by real-world objects on the ground. This rudimentary idea was refined and abstracted, first in a geometric context and later in other branches of mathematics. Over time different versions of the concept developed, but today, in a sufficiently abstract setting, we can unify these variations.^{[ citation needed ]}

In cartography, a map projection is a map of a part of the surface of the Earth onto a plane, which, in some cases, but not always, is the restriction of a projection in the above meaning. The 3D projections are also at the basis of the theory of perspective.^{[ citation needed ]}

The need for unifying the two kinds of projections and of defining the image by a central projection of any point different of the center of projection are at the origin of projective geometry. However, a projective transformation is a bijection of a projective space, a property not shared with the projections of this article.^{[ citation needed ]}

Definition

The commutativity of this diagram is the universality of the projection p, for any map f and set X. Proj-map.svg — The commutativity of this diagram is the universality of the projection $π$ , for any map $f$ and set $X$ .

Generally, a mapping where the domain and codomain are the same set (or mathematical structure) is a projection if the mapping is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a right inverse. Both notions are strongly related, as follows. Let $p$ be an idempotent mapping from a set $A$ into itself (thus $p \circ p = p$ ) and $B = p (A)$ be the image of $p$ . If we denote by $π$ the map $p$ viewed as a map from $A$ onto $B$ and by $i$ the injection of $B$ into $A$ (so that $p = i \circ π$ ), then we have $π \circ i = Id B$ (so that $π$ has a right inverse). Conversely, if $π$ has a right inverse $i$ , then $π \circ i = Id B$ implies that $i \circ π \circ i \circ π = i \circ Id B \circ π = i \circ π$ ; that is, $p = i \circ π$ is idempotent.^{[ citation needed ]}

Applications

The original notion of projection has been extended or generalized to various mathematical situations, frequently, but not always, related to geometry, for example:

In set theory:
- An operation typified by the $j$ -^th projection map, written $proj j$ , that takes an element $x = (x 1, ..., x j, ..., x n)$ of the Cartesian product $X 1 \times \dots \times X j \times \dots \times X n$ to the value $proj j (x) = x j .$ ^[1] This map is always surjective and, when each space $X k$ has a topology, this map is also continuous and open.^[2]
- A mapping that takes an element to its equivalence class under a given equivalence relation is known as the canonical projection.^[3]
- The evaluation map sends a function $f$ to the value $f (x)$ for a fixed $x$ . The space of functions $Y X$ can be identified with the Cartesian product ${\textstyle \prod _{i\in X}Y}$ , and the evaluation map is a projection map from the Cartesian product.^{[ citation needed ]}
For relational databases and query languages, the projection is a unary operation written as $\Pi _{a_{1},\ldots ,a_{n}}(R)$ where $a_{1},\ldots ,a_{n}$ is a set of attribute names. The result of such projection is defined as the set that is obtained when all tuples in $R$ are restricted to the set $\{a_{1},\ldots ,a_{n}\}$ .^[4]^[5]^[6]^{[ verification needed ]} $R$ is a database-relation.^{[ citation needed ]}
In spherical geometry, projection of a sphere upon a plane was used by Ptolemy (~150) in his Planisphaerium.^[7] The method is called stereographic projection and uses a plane tangent to a sphere and a pole C diametrically opposite the point of tangency. Any point $P$ on the sphere besides $C$ determines a line $CP$ intersecting the plane at the projected point for $P$ .^[8] The correspondence makes the sphere a one-point compactification for the plane when a point at infinity is included to correspond to $C$ , which otherwise has no projection on the plane. A common instance is the complex plane where the compactification corresponds to the Riemann sphere. Alternatively, a hemisphere is frequently projected onto a plane using the gnomonic projection.^{[ citation needed ]}
In linear algebra, a linear transformation that remains unchanged if applied twice: $p (u) = p (p (u))$ . In other words, an idempotent operator. For example, the mapping that takes a point $(x, y, z)$ in three dimensions to the point $(x, y, 0)$ is a projection. This type of projection naturally generalizes to any number of dimensions $n$ for the domain and $k \leq n$ for the codomain of the mapping. See Orthogonal projection, Projection (linear algebra). In the case of orthogonal projections, the space admits a decomposition as a product, and the projection operator is a projection in that sense as well.^[9]^[10]^{[ verification needed ]}
In differential topology, any fiber bundle includes a projection map as part of its definition. Locally at least this map looks like a projection map in the sense of the product topology and is therefore open and surjective.^{[ citation needed ]}
In topology, a retraction is a continuous map $r : X \to X$ which restricts to the identity map on its image.^[11] This satisfies a similar idempotency condition $r 2 = r$ and can be considered a generalization of the projection map. The image of a retraction is called a retract of the original space. A retraction which is homotopic to the identity is known as a deformation retraction. This term is also used in category theory to refer to any split epimorphism.^{[ citation needed ]}
The scalar projection (or resolute) of one vector onto another.^{[ citation needed ]}
In category theory, the above notion of Cartesian product of sets can be generalized to arbitrary categories. The product of some objects has a canonical projection morphism to each factor. This projection will take many forms in different categories. The projection from the Cartesian product of sets, the product topology of topological spaces (which is always surjective and open), or from the direct product of groups, etc. Although these morphisms are often epimorphisms and even surjective, they do not have to be.^[12]^{[ verification needed ]}

Related Research Articles

In mathematics, one can often define a direct product of objects already known, giving a new one. This induces a structure on the Cartesian product of the underlying sets from that of the contributing objects. More abstractly, one talks about the product in category theory, which formalizes these notions.

In mathematics, an $n$ -sphere or hypersphere is an -dimensional generalization of the -dimensional circle and -dimensional sphere to any non-negative integer . The -sphere is the setting for -dimensional spherical geometry.

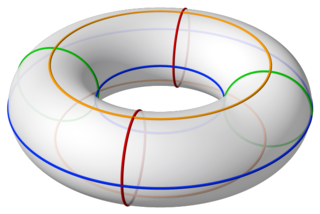
In geometry, a torus is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanar with the circle. The main types of toruses include ring toruses, horn toruses, and spindle toruses. A ring torus is sometimes colloquially referred to as a donut or doughnut.

In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine the position of the points or other geometric elements on a manifold such as Euclidean space. The order of the coordinates is significant, and they are sometimes identified by their position in an ordered tuple and sometimes by a letter, as in "the x-coordinate". The coordinates are taken to be real numbers in elementary mathematics, but may be complex numbers or elements of a more abstract system such as a commutative ring. The use of a coordinate system allows problems in geometry to be translated into problems about numbers and vice versa; this is the basis of analytic geometry.

In mathematics, a stereographic projection is a perspective projection of the sphere, through a specific point on the sphere, onto a plane perpendicular to the diameter through the point. It is a smooth, bijective function from the entire sphere except the center of projection to the entire plane. It maps circles on the sphere to circles or lines on the plane, and is conformal, meaning that it preserves angles at which curves meet and thus locally approximately preserves shapes. It is neither isometric nor equiareal.

In database theory, relational algebra is a theory that uses algebraic structures for modeling data, and defining queries on it with a well founded semantics. The theory was introduced by Edgar F. Codd.

<span class="mw-page-title-main">Quotient space (topology)</span> Topological space construction

In topology and related areas of mathematics, the quotient space of a topological space under a given equivalence relation is a new topological space constructed by endowing the quotient set of the original topological space with the quotient topology, that is, with the finest topology that makes continuous the canonical projection map. In other words, a subset of a quotient space is open if and only if its preimage under the canonical projection map is open in the original topological space.

<span class="mw-page-title-main">Fiber bundle</span> Continuous surjection satisfying a local triviality condition

In mathematics, and particularly topology, a fiber bundle is a space that is locally a product space, but globally may have a different topological structure. Specifically, the similarity between a space $and a product space is defined using a continuous surjective map, that in small regions of behaves just like a projection from corresponding regions of to The map called the projection or submersion of the bundle, is regarded as part of the structure of the bundle. The space is known as the total space of the fiber bundle, as the base space, and the fiber .$

In mathematics, a principal bundle is a mathematical object that formalizes some of the essential features of the Cartesian product $of a space with a group . In the same way as with the Cartesian product, a principal bundle is equipped with$

An action of $on, analogous to for a product space.$
A projection onto $. For a product space, this is just the projection onto the first factor, .$

In the mathematical field of differential topology, the Hopf fibration describes a 3-sphere in terms of circles and an ordinary sphere. Discovered by Heinz Hopf in 1931, it is an influential early example of a fiber bundle. Technically, Hopf found a many-to-one continuous function from the $3$ -sphere onto the $2$ -sphere such that each distinct point of the $2$ -sphere is mapped from a distinct great circle of the $3$ -sphere. Thus the $3$ -sphere is composed of fibers, where each fiber is a circle — one for each point of the $2$ -sphere.

In mathematics, the spectrum of a C*-algebra or dual of a C*-algebraA, denoted Â, is the set of unitary equivalence classes of irreducible *-representations of A. A *-representation π of A on a Hilbert space H is irreducible if, and only if, there is no closed subspace K different from H and {0} which is invariant under all operators π(x) with x ∈ A. We implicitly assume that irreducible representation means non-null irreducible representation, thus excluding trivial (i.e. identically 0) representations on one-dimensional spaces. As explained below, the spectrum Â is also naturally a topological space; this is similar to the notion of the spectrum of a ring.

In the mathematical field of algebraic topology, the homotopy groups of spheres describe how spheres of various dimensions can wrap around each other. They are examples of topological invariants, which reflect, in algebraic terms, the structure of spheres viewed as topological spaces, forgetting about their precise geometry. Unlike homology groups, which are also topological invariants, the homotopy groups are surprisingly complex and difficult to compute.

In mathematics, specifically algebraic topology, the mapping cylinder of a continuous function $between topological spaces and is the quotient$

In topology, a branch of mathematics, a retraction is a continuous mapping from a topological space into a subspace that preserves the position of all points in that subspace. The subspace is then called a retract of the original space. A deformation retraction is a mapping that captures the idea of continuously shrinking a space into a subspace.

In differential geometry, in the category of differentiable manifolds, a fibered manifold is a surjective submersion

In set theory, a projection is one of two closely related types of functions or operations, namely:

<span class="mw-page-title-main">Clifford torus</span> Geometrical object in four-dimensional space

In geometric topology, the Clifford torus is the simplest and most symmetric flat embedding of the Cartesian product of two circles $S 1 a$ and $S 1 b$ . It is named after William Kingdon Clifford. It resides in $R 4$ , as opposed to in $R 3$ . To see why $R 4$ is necessary, note that if $S 1 a$ and $S 1 b$ each exists in its own independent embedding space $R 2 a$ and $R 2 b$ , the resulting product space will be $R 4$ rather than $R 3$ . The historically popular view that the Cartesian product of two circles is an $R 3$ torus in contrast requires the highly asymmetric application of a rotation operator to the second circle, since that circle will only have one independent axis $z$ available to it after the first circle consumes $x$ and $y$ .

In category theory, a branch of mathematics, given a morphism f: X → Y and a morphism g: Z → Y, a lift or lifting of f to Z is a morphism h: X → Z such that f = g∘h. We say that f factors through h.

In mathematics, especially in the area of mathematical analysis known as dynamical systems theory, a linear flow on the torus is a flow on the n-dimensional torus

In mathematics, particularly in functional analysis, a webbed space is a topological vector space designed with the goal of allowing the results of the open mapping theorem and the closed graph theorem to hold for a wider class of linear maps whose codomains are webbed spaces. A space is called webbed if there exists a collection of sets, called a web that satisfies certain properties. Webs were first investigated by de Wilde.

References

↑ "Direct product - Encyclopedia of Mathematics". encyclopediaofmath.org. Retrieved 2021-08-11.
↑ Lee, John M. (2012). Introduction to Smooth Manifolds. Graduate Texts in Mathematics. Vol. 218 (Second ed.). p. 606. doi:10.1007/978-1-4419-9982-5. ISBN 978-1-4419-9982-5. Exercise A.32. Suppose $X_{1},\ldots ,X_{k}$ are topological spaces. Show that each projection $\pi _{i}:X_{1}\times \cdots \times X_{k}\to X_{i}$ is an open map.
↑ Brown, Arlen; Pearcy, Carl (1994-12-16). An Introduction to Analysis. Springer Science & Business Media. ISBN 978-0-387-94369-5.
↑ Alagic, Suad (2012-12-06). Relational Database Technology. Springer Science & Business Media. ISBN 978-1-4612-4922-1.
↑ Date, C. J. (2006-08-28). The Relational Database Dictionary: A Comprehensive Glossary of Relational Terms and Concepts, with Illustrative Examples. "O'Reilly Media, Inc.". ISBN 978-1-4493-9115-7.
↑ "Relational Algebra". www.cs.rochester.edu. Archived from the original on 30 January 2004. Retrieved 29 August 2021.
↑ Sidoli, Nathan; Berggren, J. L. (2007). "The Arabic version of Ptolemy's Planisphere or Flattening the Surface of the Sphere: Text, Translation, Commentary" (PDF). Sciamvs. 8. Retrieved 11 August 2021.
↑ "Stereographic projection - Encyclopedia of Mathematics". encyclopediaofmath.org. Retrieved 2021-08-11.
↑ "Projection - Encyclopedia of Mathematics". encyclopediaofmath.org. Retrieved 2021-08-11.
↑ Roman, Steven (2007-09-20). Advanced Linear Algebra. Springer Science & Business Media. ISBN 978-0-387-72831-5.
↑ "Retraction - Encyclopedia of Mathematics". encyclopediaofmath.org. Retrieved 2021-08-11.
↑ "Product of a family of objects in a category - Encyclopedia of Mathematics". encyclopediaofmath.org. Retrieved 2021-08-11.

Projection (mathematics)

Contents

Definition

Applications

Related Research Articles

References

Further reading