Perspective (graphical)

Last updated

Staircase in six-point perspective Staircase perspective.jpg
Staircase in six-point perspective
External videos
Ultima Cena - Da Vinci 5.jpg
Nuvola apps kaboodle.svg Linear Perspective: Brunelleschi's Experiment, Smarthistory [1]
Nuvola apps kaboodle.svg How One-Point Linear Perspective Works, Smarthistory [2]
Nuvola apps kaboodle.svg Empire of the Eye: The Magic of Illusion: The Trinity-Masaccio, Part 2, National Gallery of Art [3]

Linear or point-projection perspective (from Latin perspicere  'to see through') is one of two types of graphical projection perspective in the graphic arts; the other is parallel projection.[ citation needed ] Linear perspective is an approximate representation, generally on a flat surface, of an image as it is seen by the eye. Perspective drawing is useful for representing a three-dimensional scene in a two-dimensional medium, like paper.

Contents

The most characteristic features of linear perspective are that objects appear smaller as their distance from the observer increases, and that they are subject to foreshortening, meaning that an object's dimensions along the line of sight appear shorter than its dimensions across the line of sight. All objects will recede to points in the distance, usually along the horizon line, but also above and below the horizon line depending on the view used.

Italian Renaissance painters and architects including Filippo Brunelleschi, Leon Battista Alberti, Masaccio, Paolo Uccello, Piero della Francesca and Luca Pacioli studied linear perspective, wrote treatises on it, and incorporated it into their artworks.

Overview

Rays of light travel from the object, through the picture plane, and to the viewer's eye. This is the basis for graphical perspective. Perspectiva-2.svg
Rays of light travel from the object, through the picture plane, and to the viewer's eye. This is the basis for graphical perspective.

Perspective works by representing the light that passes from a scene through an imaginary rectangle (the picture plane), to the viewer's eye, as if a viewer were looking through a window and painting what is seen directly onto the windowpane. If viewed from the same spot as the windowpane was painted, the painted image would be identical to what was seen through the unpainted window. Each painted object in the scene is thus a flat, scaled down version of the object on the other side of the window. [4]

Examples of one-point perspective

A cube drawing using two-point perspective Perspective1.jpg
A cube drawing using two-point perspective

Examples of two-point perspective

A cube in three-point perspective Perspective-3point.svg
A cube in three-point perspective

Examples of three-point perspective

Examples of curvilinear perspective

Additionally, a central vanishing point can be used (just as with one-point perspective) to indicate frontal (foreshortened) depth. [5]

History

Early history

The earliest art paintings and drawings typically sized many objects and characters hierarchically according to their spiritual or thematic importance, not their distance from the viewer, and did not use foreshortening. The most important figures are often shown as the highest in a composition, also from hieratic motives, leading to the so-called "vertical perspective", common in the art of Ancient Egypt, where a group of "nearer" figures are shown below the larger figure or figures; simple overlapping was also employed to relate distance. [7] Additionally, oblique foreshortening of round elements like shields and wheels is evident in Ancient Greek red-figure pottery. [8]

Systematic attempts to evolve a system of perspective are usually considered to have begun around the fifth century BC in the art of ancient Greece, as part of a developing interest in illusionism allied to theatrical scenery. This was detailed within Aristotle's Poetics as skenographia: using flat panels on a stage to give the illusion of depth. [9] The philosophers Anaxagoras and Democritus worked out geometric theories of perspective for use with skenographia. Alcibiades had paintings in his house designed using skenographia, so this art was not confined merely to the stage. Euclid in his Optics (c. 300 BC) argues correctly that the perceived size of an object is not related to its distance from the eye by a simple proportion. [10] In the first-century BC frescoes of the Villa of P. Fannius Synistor, multiple vanishing points are used in a systematic but not fully consistent manner. [6]

Chinese artists made use of oblique projection from the first or second century until the 18th century. It is not certain how they came to use the technique; Dubery and Willats (1983) speculate that the Chinese acquired the technique from India, which acquired it from Ancient Rome, [11] while others credit it as an indigenous invention of Ancient China. [12] [13] [14] Oblique projection is also seen in Japanese art, such as in the Ukiyo-e paintings of Torii Kiyonaga (1752–1815). [11] [lower-alpha 1]

By the later periods of antiquity, artists, especially those in less popular traditions, were well aware that distant objects could be shown smaller than those close at hand for increased realism, but whether this convention was actually used in a work depended on many factors. Some of the paintings found in the ruins of Pompeii show a remarkable realism and perspective for their time. [15] It has been claimed that comprehensive systems of perspective were evolved in antiquity, but most scholars do not accept this. Hardly any of the many works where such a system would have been used have survived. A passage in Philostratus suggests that classical artists and theorists thought in terms of "circles" at equal distance from the viewer, like a classical semi-circular theatre seen from the stage. [16] The roof beams in rooms in the Vatican Virgil, from about 400 AD, are shown converging, more or less, on a common vanishing point, but this is not systematically related to the rest of the composition. [17]

Medieval artists in Europe, like those in the Islamic world and China, were aware of the general principle of varying the relative size of elements according to distance, but even more than classical art were perfectly ready to override it for other reasons. Buildings were often shown obliquely according to a particular convention. The use and sophistication of attempts to convey distance increased steadily during the period, but without a basis in a systematic theory. Byzantine art was also aware of these principles, but also used the reverse perspective convention for the setting of principal figures. Ambrogio Lorenzetti painted a floor with convergent lines in his Presentation at the Temple (1342), though the rest of the painting lacks perspective elements. [18]

Renaissance

Detail of Masolino da Panicale's St. Peter Healing a Cripple and the Raising of Tabitha (c. 1423), the earliest extant artwork known to use a consistent vanishing point Cappella brancacci, Guarigione dello storpio e resurrezione di Tabita (restaurato), Masolino.jpg
Detail of Masolino da Panicale's St. Peter Healing a Cripple and the Raising of Tabitha (c. 1423), the earliest extant artwork known to use a consistent vanishing point

It is generally accepted that Filippo Brunelleschi conducted a series of experiments between 1415 and 1420, which included making drawings of various Florentine buildings in correct perspective. [20] According to Vasari and Antonio Manetti, in about 1420, Brunelleschi demonstrated his discovery by having people look through a hole in the back of a painting he had made. Through it, they would see a building such as the Florence Baptistery. When Brunelleschi lifted a mirror in front of the viewer, it reflected his painting of the buildings which had been seen previously, so that the vanishing point was centered from the perspective of the participant. [21] Brunelleschi applied the new system of perspective to his paintings around 1425. [22]

This scenario is indicative, but faces several problems, that are still debated. First of all, nothing can be said for certain about the correctness of his perspective construction of the Baptistery of San Giovanni, because Brunelleschi's panel is lost. Second, no other perspective painting or drawing by Brunelleschi is known. (In fact, Brunelleschi was not known to have painted at all.) Third, in the account written by Antonio Manetti in his Vita di Ser Brunellesco at the end of the 15th century on Brunelleschi's panel, there is not a single occurrence of the word "experiment". Fourth, the conditions listed by Manetti are contradictory with each other. For example, the description of the eyepiece sets a visual field of 15°, much narrower than the visual field resulting from the urban landscape described. [23] [24]

Melozzo da Forli's use of upward foreshortening in his frescoes, Basilica dei Santi Apostoli, Rome, ca. 1480 Melozzo da forli, apostolo, 1480 ca., da ss. apostoli, 02.JPG
Melozzo da Forlì's use of upward foreshortening in his frescoes, Basilica dei Santi Apostoli, Rome, ca. 1480

Soon after Brunelleschi's demonstrations, nearly every interested artist in Florence and in Italy used geometrical perspective in their paintings and sculpture, [25] notably Donatello, Masaccio, [26] Lorenzo Ghiberti, Masolino da Panicale, Paolo Uccello, [26] and Filippo Lippi. Not only was perspective a way of showing depth, it was also a new method of creating a composition. Visual art could now depict a single, unified scene, rather than a combination of several. Early examples include Masolino's St. Peter Healing a Cripple and the Raising of Tabitha (c. 1423), Donatello's The Feast of Herod (c. 1427), as well as Ghiberti's Jacob and Esau and other panels from the east doors of the Florence Baptistery. [27] Masaccio (d. 1428) achieved an illusionistic effect by placing the vanishing point at the viewer's eye level in his Holy Trinity (c. 1427), [28] and in The Tribute Money , it is placed behind the face of Jesus. [29] [lower-alpha 2] In the late 15th century, Melozzo da Forlì first applied the technique of foreshortening (in Rome, Loreto, Forlì and others). [31]

This overall story is based on qualitative judgments, and would need to be faced against the material evaluations that have been conducted on Renaissance perspective paintings. Apart from the paintings of Piero della Francesca, which are a model of the genre, the majority of 15th century works show serious errors in their geometric construction. This is true of Masaccio's Trinity fresco [32] [33] and of many works, including those by renowned artists like Leonardo da Vinci. [34] [35]

As shown by the quick proliferation of accurate perspective paintings in Florence, Brunelleschi likely understood (with help from his friend the mathematician Toscanelli), [36] but did not publish, the mathematics behind perspective. Decades later, his friend Leon Battista Alberti wrote De pictura (c. 1435), a treatise on proper methods of showing distance in painting. Alberti's primary breakthrough was not to show the mathematics in terms of conical projections, as it actually appears to the eye. Instead, he formulated the theory based on planar projections, or how the rays of light, passing from the viewer's eye to the landscape, would strike the picture plane (the painting). He was then able to calculate the apparent height of a distant object using two similar triangles. The mathematics behind similar triangles is relatively simple, having been long ago formulated by Euclid. [lower-alpha 3] Alberti was also trained in the science of optics through the school of Padua and under the influence of Biagio Pelacani da Parma who studied Alhazen's Book of Optics . [37] This book, translated around 1200 into Latin, had laid the mathematical foundation for perspective in Europe. [38]

Pietro Perugino's use of perspective in Delivery of the Keys (1482), a fresco at the Sistine Chapel Entrega de las llaves a San Pedro (Perugino).jpg
Pietro Perugino's use of perspective in Delivery of the Keys  (1482), a fresco at the Sistine Chapel

Piero della Francesca elaborated on De pictura in his De Prospectiva pingendi in the 1470s, making many references to Euclid. [39] Alberti had limited himself to figures on the ground plane and giving an overall basis for perspective. Della Francesca fleshed it out, explicitly covering solids in any area of the picture plane. Della Francesca also started the now common practice of using illustrated figures to explain the mathematical concepts, making his treatise easier to understand than Alberti's. Della Francesca was also the first to accurately draw the Platonic solids as they would appear in perspective. Luca Pacioli's 1509 Divina proportione (Divine Proportion), illustrated by Leonardo da Vinci, summarizes the use of perspective in painting, including much of Della Francesca's treatise. [40] Leonardo applied one-point perspective as well as shallow focus to some of his works. [41]

Two-point perspective was demonstrated as early as 1525 by Albrecht Dürer, who studied perspective by reading Piero and Pacioli's works, in his Unterweisung der Messung ("Instruction of the Measurement"). [42]

Limitations

Satire on False Perspective by William Hogarth, 1753 William Hogarth - Absurd perspectives.png
Satire on False Perspective by William Hogarth, 1753
Example of a painting that combines various perspectives: The Frozen City (Museum of Art Aarau, Switzerland) by Matthias A. K. Zimmermann Die gefrorene Stadt.jpg
Example of a painting that combines various perspectives: The Frozen City (Museum of Art Aarau, Switzerland) by Matthias A. K. Zimmermann

Perspective images are created with reference to a particular center of vision for the picture plane. In order for the resulting image to appear identical to the original scene, a viewer must view the image from the exact vantage point used in the calculations relative to the image. When viewed from a different point, this cancels out what would appear to be distortions in the image. For example, a sphere drawn in perspective will be stretched into an ellipse. These apparent distortions are more pronounced away from the center of the image as the angle between a projected ray (from the scene to the eye) becomes more acute relative to the picture plane. Artists may choose to "correct" perspective distortions, for example by drawing all spheres as perfect circles, or by drawing figures as if centered on the direction of view. In practice, unless the viewer observes the image from an extreme angle, like standing far to the side of a painting, the perspective normally looks more or less correct. This is referred to as "Zeeman's Paradox". [43]

See also

Notes

  1. ↑ In the 18th century, Chinese artists began to combine oblique perspective with regular diminution of size of people and objects with distance; no particular vantage point is chosen, but a convincing effect is achieved. [11]
  2. ↑ Near the end of the 15th century, Leonardo da Vinci placed the vanishing point in his Last Supper behind Christ's other cheek. [30]
  3. ↑ In viewing a wall, for instance, the first triangle has a vertex at the user's eye, and vertices at the top and bottom of the wall. The bottom of this triangle is the distance from the viewer to the wall. The second, similar triangle, has a point at the viewer's eye, and has a length equal to the viewer's eye from the painting. The height of the second triangle can then be determined through a simple ratio, as proven by Euclid.

Related Research Articles

<span class="mw-page-title-main">Leonardo da Vinci</span> Italian Renaissance polymath (1452–1519)

Leonardo di ser Piero da Vinci was an Italian polymath of the High Renaissance who was active as a painter, draughtsman, engineer, scientist, theorist, sculptor, and architect. While his fame initially rested on his achievements as a painter, he also became known for his notebooks, in which he made drawings and notes on a variety of subjects, including anatomy, astronomy, botany, cartography, painting, and paleontology. Leonardo is widely regarded to have been a genius who epitomized the Renaissance humanist ideal, and his collective works comprise a contribution to later generations of artists matched only by that of his younger contemporary by 23 years Michelangelo Buonarroti.

<span class="mw-page-title-main">Luca Pacioli</span> Italian mathematician and cleric

Fra. Luca Bartolomeo de Pacioli was an Italian mathematician, Franciscan friar, collaborator with Leonardo da Vinci, and an early contributor to the field now known as accounting. He is referred to as the father of accounting and bookkeeping and he was the first person to publish a work on the double-entry system of book-keeping on the continent. He was also called Luca di Borgo after his birthplace, Borgo Sansepolcro, Tuscany.

<span class="mw-page-title-main">Masaccio</span> 15th-century Italian Renaissance painter

Masaccio, born Tommaso di Ser Giovanni di Simone, was a Florentine artist who is regarded as the first great Italian painter of the Quattrocento period of the Italian Renaissance. According to Vasari, Masaccio was the best painter of his generation because of his skill at imitating nature, recreating lifelike figures and movements as well as a convincing sense of three-dimensionality. He employed nudes and foreshortenings in his figures. This had seldom been done before him.

<span class="mw-page-title-main">Filippo Brunelleschi</span> Italian Renaissance architect (1377–1446)

Filippo di ser Brunellesco di Lippo Lapi, commonly known as Filippo Brunelleschi and also nicknamed Pippo by Leon Battista Alberti, was an Italian architect, designer, goldsmith and sculptor. He is considered to be a founding father of Renaissance architecture. He is recognized as the first modern engineer, planner, and sole construction supervisor. In 1421, Brunelleschi became the first person to receive a patent in the Western world. He is most famous for designing the dome of the Florence Cathedral, and for the mathematical technique of linear perspective in art which governed pictorial depictions of space until the late 19th century and influenced the rise of modern science. His accomplishments also include other architectural works, sculpture, mathematics, engineering, and ship design. Most surviving works can be found in Florence.

<span class="mw-page-title-main">Renaissance art</span> Visual arts produced during the European Renaissance

Renaissance art is the painting, sculpture, and decorative arts of the period of European history known as the Renaissance, which emerged as a distinct style in Italy in about AD 1400, in parallel with developments which occurred in philosophy, literature, music, science, and technology. Renaissance art took as its foundation the art of Classical antiquity, perceived as the noblest of ancient traditions, but transformed that tradition by absorbing recent developments in the art of Northern Europe and by applying contemporary scientific knowledge. Along with Renaissance humanist philosophy, it spread throughout Europe, affecting both artists and their patrons with the development of new techniques and new artistic sensibilities. For art historians, Renaissance art marks the transition of Europe from the medieval period to the Early Modern age.

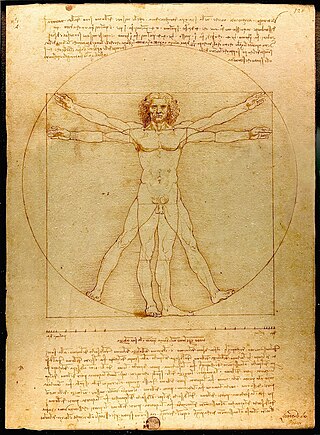
<i>Vitruvian Man</i> Drawing by Leonardo da Vinci, c. 1490

The Vitruvian Man is a drawing by the Italian Renaissance artist and scientist Leonardo da Vinci, dated to c. 1490. Inspired by the writings of the ancient Roman architect Vitruvius, the drawing depicts a nude man in two superimposed positions with his arms and legs apart and inscribed in both a circle and square. It was described by the art historian Carmen C. Bambach as "justly ranked among the all-time iconic images of Western civilization". Although not the only known drawing of a man inspired by the writings of Vitruvius, the work is a unique synthesis of artistic and scientific ideals and often considered an archetypal representation of the High Renaissance.

<span class="mw-page-title-main">Italian art</span>

Since ancient times, Greeks, Etruscans and Celts have inhabited the south, centre and north of the Italian peninsula respectively. The very numerous rock drawings in Valcamonica are as old as 8,000 BC, and there are rich remains of Etruscan art from thousands of tombs, as well as rich remains from the Greek colonies at Paestum, Agrigento and elsewhere. Ancient Rome finally emerged as the dominant Italian and European power. The Roman remains in Italy are of extraordinary richness, from the grand Imperial monuments of Rome itself to the survival of exceptionally preserved ordinary buildings in Pompeii and neighbouring sites. Following the fall of the Roman Empire, in the Middle Ages Italy remained an important centre, not only of the Carolingian art, Ottonian art of the Holy Roman Emperors, Norman art, but for the Byzantine art of Ravenna and other sites.

<span class="mw-page-title-main">Anamorphosis</span> Optical distortion used in art

Anamorphosis is a distorted projection that requires the viewer to occupy a specific vantage point, use special devices, or both to view a recognizable image. It is used in painting, photography, sculpture and installation, toys, and film special effects. The word is derived from the Greek prefix ana-, meaning "back" or "again", and the word morphe, meaning "shape" or "form". Extreme anamorphosis has been used by artists to disguise caricatures, erotic and scatological scenes, and other furtive images from a casual spectator, while revealing an undistorted image to the knowledgeable viewer.

<i>Holy Trinity</i> (Masaccio) Fresco painting by Masaccio

The Holy Trinity, with the Virgin and Saint John and donors is a fresco by the Italian Renaissance artist Masaccio in the Dominican church of Santa Maria Novella, in Florence. The fresco was among Masaccio's last major commissions and is often cited as one of the first monumental Renaissance paintings to utilize linear perspective.

<span class="mw-page-title-main">Science and inventions of Leonardo da Vinci</span> Leonardo da Vincis inventions and his relationship to science

Leonardo da Vinci (1452–1519) was an Italian polymath, regarded as the epitome of the "Renaissance Man", displaying skills in numerous diverse areas of study. While most famous for his paintings such as the Mona Lisa and the Last Supper, Leonardo is also renowned in the fields of civil engineering, chemistry, geology, geometry, hydrodynamics, mathematics, mechanical engineering, optics, physics, pyrotechnics, and zoology.

<span class="mw-page-title-main">Hockney–Falco thesis</span> Theory in art history

The Hockney–Falco thesis is a theory of art history, advanced by artist David Hockney and physicist Charles M. Falco. Both argued that advances in realism and accuracy in the history of Western art since the Renaissance were primarily the result of optical instruments such as the camera obscura, camera lucida, and curved mirrors, rather than solely due to the development of artistic technique and skill. Nineteenth-century artists' use of photography had been well documented.

<span class="mw-page-title-main">Florentine painting</span> Naturalistic painting style developed in the 14th century Florence

Florentine painting or the Florentine School refers to artists in, from, or influenced by the naturalistic style developed in Florence in the 14th century, largely through the efforts of Giotto di Bondone, and in the 15th century the leading school of Western painting. Some of the best known painters of the earlier Florentine School are Fra Angelico, Botticelli, Filippo Lippi, the Ghirlandaio family, Masolino, and Masaccio.

<span class="mw-page-title-main">Italian Renaissance painting</span> Art movement

Italian Renaissance painting is the painting of the period beginning in the late 13th century and flourishing from the early 15th to late 16th centuries, occurring in the Italian Peninsula, which was at that time divided into many political states, some independent but others controlled by external powers. The painters of Renaissance Italy, although often attached to particular courts and with loyalties to particular towns, nonetheless wandered the length and breadth of Italy, often occupying a diplomatic status and disseminating artistic and philosophical ideas.

<span class="mw-page-title-main">Themes in Italian Renaissance painting</span>

This article about the development of themes in Italian Renaissance painting is an extension to the article Italian Renaissance painting, for which it provides additional pictures with commentary. The works encompassed are from Giotto in the early 14th century to Michelangelo's Last Judgement of the 1530s.

<i>Divina proportione</i> Book on proportions by Luca Pacioli, illustrated by Leonardo da Vinci

Divina proportione, later also called De divina proportione is a book on mathematics written by Luca Pacioli and illustrated by Leonardo da Vinci, completed by February 9th, 1498 in Milan and first printed in 1509. Its subject was mathematical proportions and their applications to geometry, to visual art through perspective, and to architecture. The clarity of the written material and Leonardo's excellent diagrams helped the book to achieve an impact beyond mathematical circles, popularizing contemporary geometric concepts and images.

<span class="mw-page-title-main">Mathematics and art</span> Relationship between mathematics and art

Mathematics and art are related in a variety of ways. Mathematics has itself been described as an art motivated by beauty. Mathematics can be discerned in arts such as music, dance, painting, architecture, sculpture, and textiles. This article focuses, however, on mathematics in the visual arts.

<i>Portrait of a Man in Red Chalk</i> Drawing by Leonardo da Vinci

The portrait of a man in red chalk in the Royal Library of Turin is widely, though not universally, accepted as a self-portrait of Leonardo da Vinci. It is thought that Leonardo da Vinci drew this self-portrait at about the age of 60. The portrait has been extensively reproduced and has become an iconic representation of Leonardo as a polymath or "Renaissance Man". Despite this, some historians and scholars disagree as to the true identity of the sitter.

<i>De pictura</i> 1435 treatise by Leon Battista Alberti

De pictura is a treatise or commentarii written by the Italian humanist and artist Leon Battista Alberti. The first version, composed in Latin in 1435, was not published until 1450. It is one of his three treatises on art; the other two are De statua and De re aedificatoria, that would form the Renaissance concept for the fine arts: painting, sculpture, and architecture.

<i>Portrait of Luca Pacioli</i> Painting by Jacopo de Barbari

The Portrait of Luca Pacioli is a painting attributed to the Italian Renaissance artist Jacopo de' Barbari, dating to around 1500 and housed in the Capodimonte Museum, Naples, southern Italy. The painting portrays the Renaissance mathematician Luca Pacioli and may have been painted by his collaborator Leonardo da Vinci. The person on the right has not been identified conclusively, but could be the German painter Albrecht Dürer, whom Barbari met between 1495 and 1500.

<span class="mw-page-title-main">Museo leonardiano di Vinci</span> Museum dedicated to Leonardo da Vinci in Italy

The Museo Leonardiano di Vinci, or Leonardian Museum of Vinci, is a museum dedicated to Leonardo da Vinci, located in Vinci, Leonardo's birthplace, in the province of Florence, Italy.

References

  1. ↑ "Linear Perspective: Brunelleschi's Experiment". Smarthistory at Khan Academy. Archived from the original on 24 May 2013. Retrieved 12 May 2013.
  2. ↑ "How One-Point Linear Perspective Works". Smarthistory at Khan Academy. Archived from the original on 13 July 2013. Retrieved 12 May 2013.
  3. ↑ "Empire of the Eye: The Magic of Illusion: The Trinity-Masaccio, Part 2". National Gallery of Art at ArtBabble. Archived from the original on 1 May 2013. Retrieved 12 May 2013.
  4. ↑ D'Amelio, Joseph (2003). Perspective Drawing Handbook . Dover. p.  19. ISBN   9780486432083.
  5. ↑ "The Beginner's Guide to Perspective Drawing". The Curiously Creative. Retrieved 17 August 2019.
  6. 1 2 Hurt, Carla (9 August 2013). "Romans paint better perspective than Renaissance artists". Found in Antiquity. Retrieved 4 October 2020.
  7. ↑ Calvert, Amy. "Egyptian Art (article)". Khan Academy . Retrieved 14 May 2020.
  8. ↑ Regoli, Gigetta Dalli; Gioseffi, Decio; Mellini, Gian Lorenzo; Salvini, Roberto (1968). Vatican Museums: Rome . Italy: Newsweek. p.  22.
  9. ↑ "Skenographia in Fifth Century". CUNY. Archived from the original on 17 December 2007. Retrieved 27 December 2007.
  10. ↑ Smith, A. Mark (1999). Ptolemy and the Foundations of Ancient Mathematical Optics: A Source Based Guided Study. Philadelphia: American Philosophical Society. p. 57. ISBN   978-0-87169-893-3.
  11. 1 2 3 Cucker, Felipe (2013). Manifold Mirrors: The Crossing Paths of the Arts and Mathematics. Cambridge University Press. pp. 269–278. ISBN   978-0-521-72876-8. Dubery and Willats (1983:33) write that 'Oblique projection seems to have arrived in China from Rome by way of India round about the first or second century AD.' Figure 10.9 [Wen-Chi returns home, anon, China, 12th century] shows an archetype of the classical use of oblique perspective in Chinese painting.
  12. ↑ "Seeing History: Is perspective learned or natural?". Eclectic Light. 10 January 2018. Over the same period, the development of sophisticated and highly-detailed visual art in Asia arrived at a slightly different solution, now known as the oblique projection. Whereas Roman and subsequent European visual art effectively had multiple and incoherent vanishing points, Asian art usually lacked any vanishing point, but aligned recession in parallel. An important factor here is the use of long scrolls, which even now make fully coherent perspective projection unsuitable.
  13. ↑ Martijn de Geus (9 March 2019). "China Projections". Arch Daily. Retrieved 8 July 2020.
  14. ↑ Krikke, Jan (2 January 2018). "Why the world relies on a Chinese "perspective"". Medium.com. About 2000 years ago, the Chinese developed dengjiao toushi (等角透視), a graphic tool probably invented by Chinese architects. It came to be known in the West as axonometry. Axonometry was crucial in the development of the Chinese hand scroll painting, an art form that art historian George Rowley referred to as "the supreme creation of Chinese genius". Classic hand scroll paintings were up to ten meters in length. They are viewed by unrolling them from right to left in equal segments of about 50 cm. The painting takes the viewer through a visual story in space and time.
  15. ↑ "Pompeii. House of the Vettii. Fauces and Priapus". SUNY Buffalo. Archived from the original on 24 December 2007. Retrieved 27 December 2007.
  16. ↑ Panofsky, Erwin (1960). Renaissance and Renascences in Western Art . Stockholm: Almqvist & Wiksell. p.  122, note 1. ISBN   0-06-430026-9.
  17. ↑ Vatican Virgil image
  18. ↑ Heidi J. Hornik and Mikeal Carl Parsons, Illuminating Luke: The infancy narrative in Italian Renaissance painting, p. 132
  19. ↑ "Perspective: The Rise of Renaissance Perspective". WebExhibits. Retrieved 15 October 2020.
  20. ↑ Gärtner, Peter (1998). Brunelleschi. Cologne: Könemann. p. 23. ISBN   978-3-8290-0701-6.
  21. ↑ Edgerton 2009, pp. 44–46.
  22. ↑ Edgerton 2009, p. 40.
  23. ↑ Dominique Raynaud (1998). L'Hypothèse d'Oxford. Essai sur les origines de la perspective. Paris: Presses universitaires de France. pp. 132–141.
  24. ↑ Raynaud, Dominique (2014). Optics and the Rise of Perspective. Oxford: Bardwell Press. pp. 1–2].
  25. ↑ "...and these works (of perspective by Brunelleschi) were the means of arousing the minds of the other craftsmen, who afterwards devoted themselves to this with great zeal."
    Vasari's Lives of the Artists , chapter on Brunelleschi.
  26. 1 2 Hale, John R . (1981) [1965]. Great Ages of Man: Renaissance (rev. ed.). Time-Life. p. 98.
  27. ↑ "The Gates of Paradise: Lorenzo Ghiberti's Renaissance Masterpiece". Art Institute of Chicago . 2007. Retrieved 20 September 2020.
  28. ↑ Vasari, The Lives of the Artists, "Masaccio".
  29. ↑ Adams, Laurie (2001). Italian Renaissance Art. Oxford: Westview Press. p. 98. ISBN   978-0-8133-4902-2.
  30. ↑ White, Susan D. (2006). Draw Like Da Vinci. London: Cassell Illustrated, p. 132. ISBN   978-1-84403-444-4.
  31. ↑ Harness, Brenda. "Melozzo da Forli: Master of Foreshortening". Fine Art Touch. Retrieved 15 October 2020.
  32. ↑ Field, J. V.; Lunardi, R.; Settle, T. B. (1989). "The perspective scheme of Masaccio's Trinity fresco". Nuncius. 4 (2): 31–118. doi:10.1163/182539189X00680. INIST   11836604.
  33. ↑ Dominique Raynaud (1998). L'Hypothèse d'Oxford. Paris: Presses universitaires de France. pp. 72–120.
  34. ↑ Raynaud, Dominique (2016). "Fact and Fiction Regarding Masaccio's Trinity Fresco". Studies on Binocular Vision. Archimedes. Vol. 47. pp. 53–67. doi:10.1007/978-3-319-42721-8_4. ISBN   978-3-319-42720-1.
  35. ↑ Raynaud, Dominique (2020). "Las fuentes ópticas de Leonardo". In Ramón-Laca, Luis (ed.). Leonardo da Vinci. Perspectiva y visión. Alcalá de Henares: UAH. pp. 61–62. ISBN   978-84-18254-89-5. OCLC   1243556932.
  36. ↑ Vasari, Giorgio (1885). Stories of the Italian Artists. Scribner & Welford. p. 53. Messer Paolo dal Pozzo Toscanelli, having returned from his studies, invited Filippo with other friends to supper in a garden, and the discourse falling on mathematical subjects, Filippo formed a friendship with him and learned geometry from him.
  37. ↑ El-Bizri, Nader (2010). "Classical Optics and the Perspectiva Traditions Leading to the Renaissance". In Hendrix, John Shannon; Carman, Charles H. (eds.). Renaissance Theories of Vision (Visual Culture in Early Modernity) . Farnham, Surrey: Ashgate Publishing. pp.  11–30. ISBN   978-1-409400-24-0.
  38. ↑ Hans, Belting (2011). Florence and Baghdad: Renaissance art and Arab science (1st English ed.). Cambridge, Massachusetts: Belknap Press of Harvard University Press. pp. 90–92. ISBN   978-0-674-05004-4. OCLC   701493612.
  39. ↑ Livio, Mario (2003). The Golden Ratio. New York: Broadway Books. p. 126. ISBN   0-7679-0816-3.
  40. ↑ O'Connor, J. J.; Robertson, E. F. (July 1999). "Luca Pacioli". University of St Andrews. Archived from the original on 22 September 2015. Retrieved 23 September 2015.
  41. ↑ Goldstein, Andrew M. (17 November 2011). "The Male "Mona Lisa"?: Art Historian Martin Kemp on Leonardo da Vinci's Mysterious "Salvator Mundi"". Blouin Artinfo.
  42. ↑ MacKinnon, Nick (1993). "The Portrait of Fra Luca Pacioli". The Mathematical Gazette . 77 (479): 206. doi:10.2307/3619717. JSTOR   3619717. S2CID   195006163.
  43. ↑ "Handprint : Perspective in the world". Archived from the original on 6 January 2007. Retrieved 25 December 2006. Retrieved on 25 December 2006

Sources

Further reading

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.