In computing, a compiler is a computer program that translates computer code written in one programming language into another language. The name "compiler" is primarily used for programs that translate source code from a high-level programming language to a low-level programming language to create an executable program.
A mathematical model is an abstract description of a concrete system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used in applied mathematics and in the natural sciences and engineering disciplines, as well as in non-physical systems such as the social sciences (such as economics, psychology, sociology, political science). It can also be taught as a subject in its own right.

Supervised learning (SL) is a paradigm in machine learning where input objects and a desired output value train a model. The training data is processed, building a function that maps new data on expected output values. An optimal scenario will allow for the algorithm to correctly determine output values for unseen instances. This requires the learning algorithm to generalize from the training data to unseen situations in a "reasonable" way. This statistical quality of an algorithm is measured through the so-called generalization error.

In computer science, a search algorithm is an algorithm designed to solve a search problem. Search algorithms work to retrieve information stored within particular data structure, or calculated in the search space of a problem domain, with either discrete or continuous values.
In computing, an optimizing compiler is a compiler that tries to minimize or maximize some attributes of an executable computer program. Common requirements are to minimize a program's execution time, memory footprint, storage size, and power consumption.

Mathematical optimization or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries.
In computer science, program optimization, code optimization, or software optimization is the process of modifying a software system to make some aspect of it work more efficiently or use fewer resources. In general, a computer program may be optimized so that it executes more rapidly, or to make it capable of operating with less memory storage or other resources, or draw less power.
Sensitivity analysis is the study of how the uncertainty in the output of a mathematical model or system can be divided and allocated to different sources of uncertainty in its inputs. A related practice is uncertainty analysis, which has a greater focus on uncertainty quantification and propagation of uncertainty; ideally, uncertainty and sensitivity analysis should be run in tandem.
In mathematics, nonlinear programming (NLP) is the process of solving an optimization problem where some of the constraints or the objective function are nonlinear. An optimization problem is one of calculation of the extrema of an objective function over a set of unknown real variables and conditional to the satisfaction of a system of equalities and inequalities, collectively termed constraints. It is the sub-field of mathematical optimization that deals with problems that are not linear.
In mathematics, computer science and economics, an optimization problem is the problem of finding the best solution from all feasible solutions.
In statistics, classification is the problem of identifying which of a set of categories (sub-populations) an observation belongs to. Examples are assigning a given email to the "spam" or "non-spam" class, and assigning a diagnosis to a given patient based on observed characteristics of the patient.
Design Closure is a part of the digital electronic design automation workflow by which an integrated circuit design is modified from its initial description to meet a growing list of design constraints and objectives.
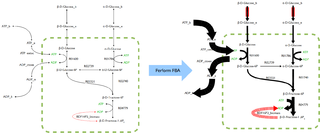
Flux balance analysis (FBA) is a mathematical method for simulating metabolism in genome-scale reconstructions of metabolic networks. In comparison to traditional methods of modeling, FBA is less intensive in terms of the input data required for constructing the model. Simulations performed using FBA are computationally inexpensive and can calculate steady-state metabolic fluxes for large models in a few seconds on modern personal computers. The related method of metabolic pathway analysis seeks to find and list all possible pathways between metabolites.
Interprocedural optimization (IPO) is a collection of compiler techniques used in computer programming to improve performance in programs containing many frequently used functions of small or medium length. IPO differs from other compiler optimizations by analyzing the entire program as opposed to a single function or block of code.
Goals-Based Investing or Goal-Driven Investing is the use of financial markets to fund goals within a specified period of time. Traditional portfolio construction balances expected portfolio variance with return and uses a risk aversion metric to select the optimal mix of investments. By contrast, GBI optimizes an investment mix to minimize the probability of failing to achieve a minimum wealth level within a set period of time.
A Gödel machine is a hypothetical self-improving computer program that solves problems in an optimal way. It uses a recursive self-improvement protocol in which it rewrites its own code when it can prove the new code provides a better strategy. The machine was invented by Jürgen Schmidhuber, but is named after Kurt Gödel who inspired the mathematical theories.
OptimJ is an extension for Java with language support for writing optimization models and abstractions for bulk data processing. The extensions and the proprietary product implementing the extensions were developed by Ateji which went out of business in September 2011. OptimJ aims at providing a clear and concise algebraic notation for optimization modeling, removing compatibility barriers between optimization modeling and application programming tools, and bringing software engineering techniques such as object-orientation and modern IDE support to optimization experts.
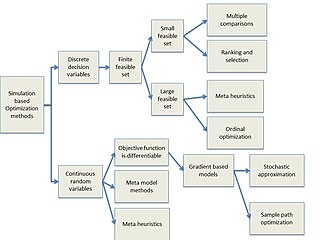
Simulation-based optimization integrates optimization techniques into simulation modeling and analysis. Because of the complexity of the simulation, the objective function may become difficult and expensive to evaluate. Usually, the underlying simulation model is stochastic, so that the objective function must be estimated using statistical estimation techniques.
Quantum optimization algorithms are quantum algorithms that are used to solve optimization problems. Mathematical optimization deals with finding the best solution to a problem from a set of possible solutions. Mostly, the optimization problem is formulated as a minimization problem, where one tries to minimize an error which depends on the solution: the optimal solution has the minimal error. Different optimization techniques are applied in various fields such as mechanics, economics and engineering, and as the complexity and amount of data involved rise, more efficient ways of solving optimization problems are needed. Quantum computing may allow problems which are not practically feasible on classical computers to be solved, or suggest a considerable speed up with respect to the best known classical algorithm.




