
In mathematics and computer science, graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of vertices which are connected by edges. A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically. Graphs are one of the principal objects of study in discrete mathematics.
A Bayesian network is a probabilistic graphical model that represents a set of variables and their conditional dependencies via a directed acyclic graph (DAG). While it is one of several forms of causal notation, causal networks are special cases of Bayesian networks. Bayesian networks are ideal for taking an event that occurred and predicting the likelihood that any one of several possible known causes was the contributing factor. For example, a Bayesian network could represent the probabilistic relationships between diseases and symptoms. Given symptoms, the network can be used to compute the probabilities of the presence of various diseases.
A graphical model or probabilistic graphical model (PGM) or structured probabilistic model is a probabilistic model for which a graph expresses the conditional dependence structure between random variables. They are commonly used in probability theory, statistics—particularly Bayesian statistics—and machine learning.
DOT is a graph description language, developed as a part of the Graphviz project. DOT graphs are typically stored as files with the .gv or .dot filename extension — .gv is preferred, to avoid confusion with the .dot extension used by versions of Microsoft Word before 2007. dot is also the name of the main program to process DOT files in the Graphviz package.

In mathematics, computer science and network science, network theory is a part of graph theory. It defines networks as graphs where the vertices or edges possess attributes. Network theory analyses these networks over the symmetric relations or asymmetric relations between their (discrete) components.
In computer science, graph transformation, or graph rewriting, concerns the technique of creating a new graph out of an original graph algorithmically. It has numerous applications, ranging from software engineering to layout algorithms and picture generation.

In the context of network theory, a complex network is a graph (network) with non-trivial topological features—features that do not occur in simple networks such as lattices or random graphs but often occur in networks representing real systems. The study of complex networks is a young and active area of scientific research inspired largely by empirical findings of real-world networks such as computer networks, biological networks, technological networks, brain networks, climate networks and social networks.
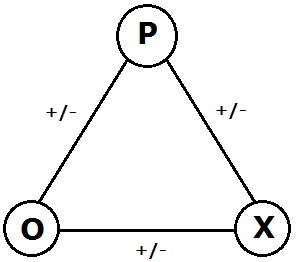
In the area of graph theory in mathematics, a signed graph is a graph in which each edge has a positive or negative sign.
Graph Modeling Language (GML) is a hierarchical ASCII-based file format for describing graphs. It has been also named Graph Meta Language.
In computing, a sink, or data sink generally refers to the destination of data flow.
Dynamic network analysis (DNA) is an emergent scientific field that brings together traditional social network analysis (SNA), link analysis (LA), social simulation and multi-agent systems (MAS) within network science and network theory. Dynamic networks are a function of time to a set of graphs; for each time point there is a graph. This is akin to the definition of dynamical systems, in which the function is from time to an ambient space, where instead of ambient space time is translated to relationships between pairs of vertices.
An object-based spatial database is a spatial database that stores the location as objects. The object-based spatial model treats the world as surface littered with recognizable objects, which exist independent of their locations.
In computing, reactive programming is a declarative programming paradigm concerned with data streams and the propagation of change. With this paradigm, it is possible to express static or dynamic data streams with ease, and also communicate that an inferred dependency within the associated execution model exists, which facilitates the automatic propagation of the changed data flow.

Network science is an academic field which studies complex networks such as telecommunication networks, computer networks, biological networks, cognitive and semantic networks, and social networks, considering distinct elements or actors represented by nodes and the connections between the elements or actors as links. The field draws on theories and methods including graph theory from mathematics, statistical mechanics from physics, data mining and information visualization from computer science, inferential modeling from statistics, and social structure from sociology. The United States National Research Council defines network science as "the study of network representations of physical, biological, and social phenomena leading to predictive models of these phenomena."
A graph database (GDB) is a database that uses graph structures for semantic queries with nodes, edges, and properties to represent and store data. A key concept of the system is the graph. The graph relates the data items in the store to a collection of nodes and edges, the edges representing the relationships between the nodes. The relationships allow data in the store to be linked together directly and, in many cases, retrieved with one operation. Graph databases hold the relationships between data as a priority. Querying relationships is fast because they are perpetually stored in the database. Relationships can be intuitively visualized using graph databases, making them useful for heavily inter-connected data.

NetworkX is a Python library for studying graphs and networks. NetworkX is free software released under the BSD-new license.
Cypher is a declarative graph query language that allows for expressive and efficient data querying in a property graph.
In graph theory and network analysis, node influence metrics are measures that rank or quantify the influence of every node within a graph. They are related to centrality indices. Applications include measuring the influence of each person in a social network, understanding the role of infrastructure nodes in transportation networks, the Internet, or urban networks, and the participation of a given node in disease dynamics.
The field of complex networks has emerged as an important area of science to generate novel insights into nature of complex systems The application of network theory to climate science is a young and emerging field. To identify and analyze patterns in global climate, scientists model climate data as complex networks.
Dual phase evolution (DPE) is a process that drives self-organization within complex adaptive systems. It arises in response to phase changes within the network of connections formed by a system's components. DPE occurs in a wide range of physical, biological and social systems. Its applications to technology include methods for manufacturing novel materials and algorithms to solve complex problems in computation.








