
In mathematics, graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of vertices which are connected by edges. A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically. Graphs are one of the principal objects of study in discrete mathematics.

A minimum spanning tree (MST) or minimum weight spanning tree is a subset of the edges of a connected, edge-weighted undirected graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight. That is, it is a spanning tree whose sum of edge weights is as small as possible. More generally, any edge-weighted undirected graph has a minimum spanning forest, which is a union of the minimum spanning trees for its connected components.

In graph theory, the shortest path problem is the problem of finding a path between two vertices in a graph such that the sum of the weights of its constituent edges is minimized.

Dijkstra's algorithm is an algorithm for finding the shortest paths between nodes in a graph, which may represent, for example, road networks. It was conceived by computer scientist Edsger W. Dijkstra in 1956 and published three years later.
In computer science, the Floyd–Warshall algorithm is an algorithm for finding shortest paths in a directed weighted graph with positive or negative edge weights. A single execution of the algorithm will find the lengths of shortest paths between all pairs of vertices. Although it does not return details of the paths themselves, it is possible to reconstruct the paths with simple modifications to the algorithm. Versions of the algorithm can also be used for finding the transitive closure of a relation , or widest paths between all pairs of vertices in a weighted graph.

In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets and such that every edge connects a vertex in to one in . Vertex sets and are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.

In graph theory, a component of an undirected graph is a connected subgraph that is not part of any larger connected subgraph. The components of any graph partition its vertices into disjoint sets, and are the induced subgraphs of those sets. A graph that is itself connected has exactly one component, consisting of the whole graph. Components are also sometimes called connected components.

In the mathematical field of graph theory, a spanning treeT of an undirected graph G is a subgraph that is a tree which includes all of the vertices of G. In general, a graph may have several spanning trees, but a graph that is not connected will not contain a spanning tree. If all of the edges of G are also edges of a spanning tree T of G, then G is a tree and is identical to T.

The Steiner tree problem, or minimum Steiner tree problem, named after Jakob Steiner, is an umbrella term for a class of problems in combinatorial optimization. While Steiner tree problems may be formulated in a number of settings, they all require an optimal interconnect for a given set of objects and a predefined objective function. One well-known variant, which is often used synonymously with the term Steiner tree problem, is the Steiner tree problem in graphs. Given an undirected graph with non-negative edge weights and a subset of vertices, usually referred to as terminals, the Steiner tree problem in graphs requires a tree of minimum weight that contains all terminals. Further well-known variants are the Euclidean Steiner tree problem and the rectilinear minimum Steiner tree problem.
In the mathematical discipline of graph theory, a matching or independent edge set in an undirected graph is a set of edges without common vertices. Finding a matching in a bipartite graph can be treated as a network flow problem.

In graph theory, a path in a graph is a finite or infinite sequence of edges which joins a sequence of vertices which, by most definitions, are all distinct. A directed path in a directed graph is a finite or infinite sequence of edges which joins a sequence of distinct vertices, but with the added restriction that the edges be all directed in the same direction.
In the mathematical subfield of graph theory a level structure of an undirected graph is a partition of the vertices into subsets that have the same distance from a given root vertex.
In the mathematical field of graph theory, the distance between two vertices in a graph is the number of edges in a shortest path connecting them. This is also known as the geodesic distance or shortest-path distance. Notice that there may be more than one shortest path between two vertices. If there is no path connecting the two vertices, i.e., if they belong to different connected components, then conventionally the distance is defined as infinite.
Johnson's algorithm is a way to find the shortest paths between all pairs of vertices in an edge-weighted directed graph. It allows some of the edge weights to be negative numbers, but no negative-weight cycles may exist. It works by using the Bellman–Ford algorithm to compute a transformation of the input graph that removes all negative weights, allowing Dijkstra's algorithm to be used on the transformed graph. It is named after Donald B. Johnson, who first published the technique in 1977.
In graph theory, a cut is a partition of the vertices of a graph into two disjoint subsets. Any cut determines a cut-set, the set of edges that have one endpoint in each subset of the partition. These edges are said to cross the cut. In a connected graph, each cut-set determines a unique cut, and in some cases cuts are identified with their cut-sets rather than with their vertex partitions.
In chemical graph theory, the Wiener index introduced by Harry Wiener, is a topological index of a molecule, defined as the sum of the lengths of the shortest paths between all pairs of vertices in the chemical graph representing the non-hydrogen atoms in the molecule.
In computer science, the method of contraction hierarchies is a speed-up technique for finding the shortest-path in a graph. The most intuitive applications are car-navigation systems: a user wants to drive from to using the quickest possible route. The metric optimized here is the travel time. Intersections are represented by vertices, the road sections connecting them by edges. The edge weights represent the time it takes to drive along this segment of the road. A path from to is a sequence of edges ; the shortest path is the one with the minimal sum of edge weights among all possible paths. The shortest path in a graph can be computed using Dijkstra's algorithm but, given that road networks consist of tens of millions of vertices, this is impractical. Contraction hierarchies is a speed-up method optimized to exploit properties of graphs representing road networks. The speed-up is achieved by creating shortcuts in a preprocessing phase which are then used during a shortest-path query to skip over "unimportant" vertices. This is based on the observation that road networks are highly hierarchical. Some intersections, for example highway junctions, are "more important" and higher up in the hierarchy than for example a junction leading into a dead end. Shortcuts can be used to save the precomputed distance between two important junctions such that the algorithm doesn't have to consider the full path between these junctions at query time. Contraction hierarchies do not know about which roads humans consider "important", but they are provided with the graph as input and are able to assign importance to vertices using heuristics.
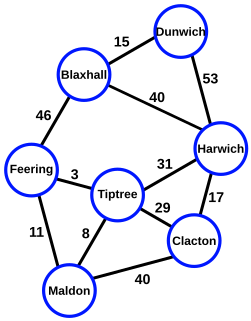
In graph algorithms, the widest path problem is the problem of finding a path between two designated vertices in a weighted graph, maximizing the weight of the minimum-weight edge in the path. The widest path problem is also known as the maximum capacity path problem. It is possible to adapt most shortest path algorithms to compute widest paths, by modifying them to use the bottleneck distance instead of path length. However, in many cases even faster algorithms are possible.
In graph theory, betweenness centrality is a measure of centrality in a graph based on shortest paths. For every pair of vertices in a connected graph, there exists at least one shortest path between the vertices such that either the number of edges that the path passes through or the sum of the weights of the edges is minimized. The betweenness centrality for each vertex is the number of these shortest paths that pass through the vertex.
In network theory, the Wiener connector is a means of maximizing efficiency in connecting specified "query vertices" in a network. Given a connected, undirected graph and a set of query vertices in a graph, the minimum Wiener connector is an induced subgraph that connects the query vertices and minimizes the sum of shortest path distances among all pairs of vertices in the subgraph. In combinatorial optimization, the minimum Wiener connector problem is the problem of finding the minimum Wiener connector. It can be thought of as a version of the classic Steiner tree problem, where instead of minimizing the size of the tree, the objective is to minimize the distances in the subgraph.











