| Great triakis octahedron | |
|---|---|
 | |
| Type | Star polyhedron |
| Face |  |
| Elements | F = 24, E = 36 V = 14 (χ = 2) |
| Symmetry group | Oh, [4,3], *432 |
| Index references | DU 19 |
| dual polyhedron | Stellated truncated hexahedron |
In geometry, the great triakis octahedron is the dual of the stellated truncated hexahedron (U19). It has 24 intersecting isosceles triangle faces. Part of each triangle lies within the solid, hence is invisible in solid models.
The triangles have one angle of and two of . The dihedral angle equals .
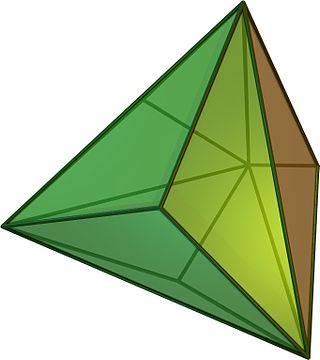
In geometry, a triakis tetrahedron is a Catalan solid with 12 faces. Each Catalan solid is the dual of an Archimedean solid. The dual of the triakis tetrahedron is the truncated tetrahedron.
In geometry, a triakis octahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated cube.
In geometry, the deltoidal icositetrahedron is a Catalan solid. Its 24 faces are congruent kites. The deltoidal icositetrahedron, whose dual is the (uniform) rhombicuboctahedron, is tightly related to the pseudo-deltoidal icositetrahedron, whose dual is the pseudorhombicuboctahedron; but the actual and pseudo-d.i. are not to be confused with each other.
In geometry, a disdyakis dodecahedron,, is a Catalan solid with 48 faces and the dual to the Archimedean truncated cuboctahedron. As such it is face-transitive but with irregular face polygons. It resembles an augmented rhombic dodecahedron. Replacing each face of the rhombic dodecahedron with a flat pyramid creates a polyhedron that looks almost like the disdyakis dodecahedron, and is topologically equivalent to it. More formally, the disdyakis dodecahedron is the Kleetope of the rhombic dodecahedron. The net of the rhombic dodecahedral pyramid also shares the same topology.
In geometry, a pentagonal hexecontahedron is a Catalan solid, dual of the snub dodecahedron. It has two distinct forms, which are mirror images of each other. It has 92 vertices that span 60 pentagonal faces. It is the Catalan solid with the most vertices. Among the Catalan and Archimedean solids, it has the second largest number of vertices, after the truncated icosidodecahedron, which has 120 vertices.
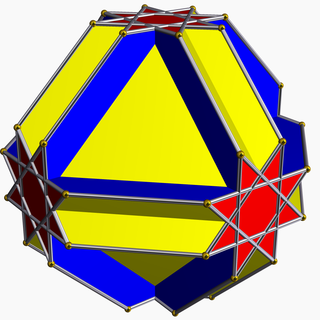
In geometry, the cubitruncated cuboctahedron or cuboctatruncated cuboctahedron is a nonconvex uniform polyhedron, indexed as U16. It has 20 faces (8 hexagons, 6 octagons, and 6 octagrams), 72 edges, and 48 vertices,and has a shäfli symbol of tr{4,3/2}
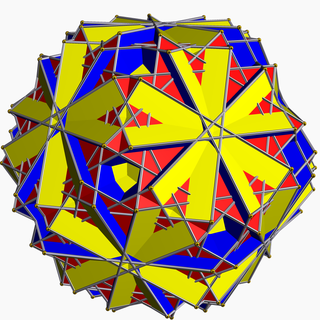
In geometry, the great truncated icosidodecahedron (or great quasitruncated icosidodecahedron or stellatruncated icosidodecahedron) is a nonconvex uniform polyhedron, indexed as U68. It has 62 faces (30 squares, 20 hexagons, and 12 decagrams), 180 edges, and 120 vertices. It is given a Schläfli symbol t0,1,2{5⁄3,3}, and Coxeter-Dynkin diagram, .
In geometry, the tridyakis icosahedron is the dual polyhedron of the nonconvex uniform polyhedron, icositruncated dodecadodecahedron. It has 44 vertices, 180 edges, and 120 scalene triangular faces.
In geometry, the great rhombic triacontahedron is a nonconvex isohedral, isotoxal polyhedron. It is the dual of the great icosidodecahedron (U54). Like the convex rhombic triacontahedron it has 30 rhombic faces, 60 edges and 32 vertices.
In geometry, the great hexacronic icositetrahedron is the dual of the great cubicuboctahedron. Its faces are kites. Part of each kite lies inside the solid, hence is invisible in solid models.
In geometry, the great deltoidal icositetrahedron is the dual of the nonconvex great rhombicuboctahedron. Its faces are darts. Part of each dart lies inside the solid, hence is invisible in solid models.
In geometry, the small rhombihexacron is the dual of the small rhombihexahedron. It is visually identical to the small hexacronic icositetrahedron. Its faces are antiparallelograms formed by pairs of coplanar triangles.
In geometry, the small hexacronic icositetrahedron is the dual of the small cubicuboctahedron. It is visually identical to the small rhombihexacron. A part of each dart lies inside the solid, hence is invisible in solid models.
In geometry, the great rhombihexacron (or great dipteral disdodecahedron) is a nonconvex isohedral polyhedron. It is the dual of the uniform great rhombihexahedron (U21). It has 24 identical bow-tie-shaped faces, 18 vertices, and 48 edges.
In geometry, the small stellapentakis dodecahedron is a nonconvex isohedral polyhedron. It is the dual of the truncated great dodecahedron. It has 60 intersecting triangular faces.
In geometry, the great stellapentakis dodecahedron is a nonconvex isohedral polyhedron. It is the dual of the truncated great icosahedron. It has 60 intersecting triangular faces.
In geometry, the great triakis icosahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform great stellated truncated dodecahedron. Its faces are isosceles triangles. Part of each triangle lies within the solid, hence is invisible in solid models.
In geometry, the great disdyakis dodecahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform great truncated cuboctahedron. It has 48 triangular faces.
In geometry, the great pentakis dodecahedron is a nonconvex isohedral polyhedron.
In geometry, the medial disdyakis triacontahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform truncated dodecadodecahedron. It has 120 triangular faces.
 | This polyhedron-related article is a stub. You can help Wikipedia by expanding it. |
