Related Research Articles

Gregory John Chaitin is an Argentine-American mathematician and computer scientist. Beginning in the late 1960s, Chaitin made contributions to algorithmic information theory and metamathematics, in particular a computer-theoretic result equivalent to Gödel's incompleteness theorem. He is considered to be one of the founders of what is today known as algorithmic complexity together with Andrei Kolmogorov and Ray Solomonoff. Along with the works of e.g. Solomonoff, Kolmogorov, Martin-Löf, and Leonid Levin, algorithmic information theory became a foundational part of theoretical computer science, information theory, and mathematical logic. It is a common subject in several computer science curricula. Besides computer scientists, Chaitin's work draws attention of many philosophers and mathematicians to fundamental problems in mathematical creativity and digital philosophy.
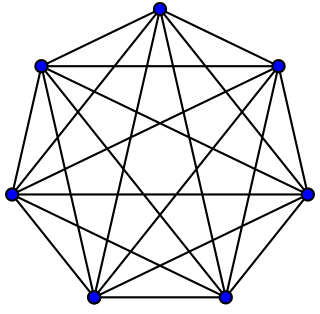
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge. A complete digraph is a directed graph in which every pair of distinct vertices is connected by a pair of unique edges.

A greedy algorithm is any algorithm that follows the problem-solving heuristic of making the locally optimal choice at each stage. In many problems, a greedy strategy does not produce an optimal solution, but a greedy heuristic can yield locally optimal solutions that approximate a globally optimal solution in a reasonable amount of time.

In mathematics, particularly graph theory, and computer science, a directed acyclic graph (DAG) is a directed graph with no directed cycles. That is, it consists of vertices and edges, with each edge directed from one vertex to another, such that following those directions will never form a closed loop. A directed graph is a DAG if and only if it can be topologically ordered, by arranging the vertices as a linear ordering that is consistent with all edge directions. DAGs have numerous scientific and computational applications, ranging from biology to information science to computation (scheduling).
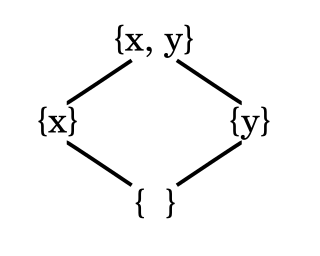
In order theory, a Hasse diagram is a type of mathematical diagram used to represent a finite partially ordered set, in the form of a drawing of its transitive reduction. Concretely, for a partially ordered set one represents each element of as a vertex in the plane and draws a line segment or curve that goes upward from one vertex to another vertex whenever covers . These curves may cross each other but must not touch any vertices other than their endpoints. Such a diagram, with labeled vertices, uniquely determines its partial order.
Given a directed graph G = (V, E), a path cover is a set of directed paths such that every vertex v ∈ V belongs to at least one path. Note that a path cover may include paths of length 0 (a single vertex).

Egon Börger is a German-born computer scientist based in Italy.

David Arthur Eppstein is an American computer scientist and mathematician. He is a distinguished professor of computer science at the University of California, Irvine. He is known for his work in computational geometry, graph algorithms, and recreational mathematics. In 2011, he was named an ACM Fellow.

Noga Alon is an Israeli mathematician and a professor of mathematics at Princeton University noted for his contributions to combinatorics and theoretical computer science, having authored hundreds of papers.

Jaroslav (Jarik) Nešetřil is a Czech mathematician, working at Charles University in Prague. His research areas include combinatorics, graph theory, algebra, posets, computer science.
In graph theory, an arborescence is a directed graph having a distinguished vertex u such that, for any other vertex v, there is exactly one directed path from u to v. An arborescence is thus the directed-graph form of a rooted tree, understood here as an undirected graph. An arborescence is also a directed rooted tree in which all edges point away from the root; a number of other equivalent characterizations exist.

Martin Charles Golumbic is a mathematician and computer scientist known for his research on perfect graphs, graph sandwich problems, compiler optimization, and spatial-temporal reasoning. He is a professor emeritus of computer science at the University of Haifa, and was the founder of the journal Annals of Mathematics and Artificial Intelligence.
Michael Ralph Fellows AC HFRSNZ MAE is a computer scientist and the Elite Professor of Computer Science in the Department of Informatics at the University of Bergen, Norway as of January 2016.

In a graph, a maximum cut is a cut whose size is at least the size of any other cut. That is, it is a partition of the graph's vertices into two complementary sets S and T, such that the number of edges between S and T is as large as possible. Finding such a cut is known as the max-cut problem.
In the mathematical fields of graph theory and combinatorial optimization, the bipartite dimension or biclique cover number of a graph G = (V, E) is the minimum number of bicliques (that is complete bipartite subgraphs), needed to cover all edges in E. A collection of bicliques covering all edges in G is called a biclique edge cover, or sometimes biclique cover. The bipartite dimension of G is often denoted by the symbol d(G).

In mathematics, and more specifically in graph theory, a directed graph is a graph that is made up of a set of vertices connected by directed edges, often called arcs.

Grzegorz Rozenberg is a Polish and Dutch computer scientist.

In graph theory, an ear of an undirected graph G is a path P where the two endpoints of the path may coincide, but where otherwise no repetition of edges or vertices is allowed, so every internal vertex of P has degree two in G. An ear decomposition of an undirected graph G is a partition of its set of edges into a sequence of ears, such that the one or two endpoints of each ear belong to earlier ears in the sequence and such that the internal vertices of each ear do not belong to any earlier ear. Additionally, in most cases the first ear in the sequence must be a cycle. An open ear decomposition or a proper ear decomposition is an ear decomposition in which the two endpoints of each ear after the first are distinct from each other.

Peter D. Eades is an Australian computer scientist, an emeritus professor in the School of Information Technologies at the University of Sydney, known for his expertise in graph drawing.
Dorothea Wagner is a German computer scientist, known for her research in graph drawing, route planning, and social network analysis. She heads the Institute of Theoretical Informatics at the Karlsruhe Institute of Technology.
References
- ↑ "Gregory Gutin". Royal Society. Retrieved 10 July 2017.
- ↑ "Symposium on Access control Models and Technologies". Sacmat.org. Retrieved 10 July 2017.
- ↑ "Symposium on Access control Models and Technologies". Sacmat.org. Retrieved 10 July 2017.
- ↑ "Symposium on Access control Models and Technologies". Sacmat.org. Retrieved 21 March 2022.
- ↑ "Gregory Gutin's 60th Birthday ConferenceGregory Gutin's 60th Birthday Conference | January 7th & 8th 2017". Gutin60.ma.rhul.ac.uk. 8 January 2017. Retrieved 10 July 2017.
- ↑ "G. Gutin's Academia Europaea webpage".