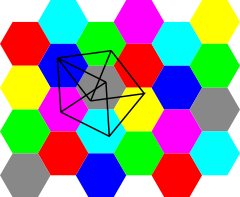
In mathematics, the four color theorem, or the four color map theorem, states that no more than four colors are required to color the regions of any map so that no two adjacent regions have the same color. Adjacent means that two regions share a common boundary of non-zero length. It was the first major theorem to be proved using a computer. Initially, this proof was not accepted by all mathematicians because the computer-assisted proof was infeasible for a human to check by hand. The proof has gained wide acceptance since then, although some doubts remain.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.

Hugo Hadwiger was a Swiss mathematician, known for his work in geometry, combinatorics, and cryptography.

In graph theory, a proper edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most k different colors, for a given value of k, or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three.

In graph theory, the Erdős–Faber–Lovász conjecture is a problem about graph coloring, named after Paul Erdős, Vance Faber, and László Lovász, who formulated it in 1972. It says:

In graph theory, a circle graph is the intersection graph of a chord diagram. That is, it is an undirected graph whose vertices can be associated with a finite system of chords of a circle such that two vertices are adjacent if and only if the corresponding chords cross each other.

In graph theory, the Hadwiger conjecture states that if is loopless and has no minor then its chromatic number satisfies . It is known to be true for . The conjecture is a generalization of the four-color theorem and is considered to be one of the most important and challenging open problems in the field.

In graph theory, the Hadwiger number of an undirected graph G is the size of the largest complete graph that can be obtained by contracting edges of G. Equivalently, the Hadwiger number h(G) is the largest number n for which the complete graph Kn is a minor of G, a smaller graph obtained from G by edge contractions and vertex and edge deletions. The Hadwiger number is also known as the contraction clique number of G or the homomorphism degree of G. It is named after Hugo Hadwiger, who introduced it in 1943 in conjunction with the Hadwiger conjecture, which states that the Hadwiger number is always at least as large as the chromatic number of G.

In mathematics, particularly geometric graph theory, a unit distance graph is a graph formed from a collection of points in the Euclidean plane by connecting two points whenever the distance between them is exactly one. To distinguish these graphs from a broader definition that allows some non-adjacent pairs of vertices to be at distance one, they may also be called strict unit distance graphs or faithful unit distance graphs. As a hereditary family of graphs, they can be characterized by forbidden induced subgraphs. The unit distance graphs include the cactus graphs, the matchstick graphs and penny graphs, and the hypercube graphs. The generalized Petersen graphs are non-strict unit distance graphs.
In geometry, the Beckman–Quarles theorem states that if a transformation of the Euclidean plane or a higher-dimensional Euclidean space preserves unit distances, then it preserves all Euclidean distances. Equivalently, every homomorphism from the unit distance graph of the plane to itself must be an isometry of the plane. The theorem is named after Frank S. Beckman and Donald A. Quarles Jr., who published this result in 1953; it was later rediscovered by other authors and re-proved in multiple ways. Analogous theorems for rational subsets of Euclidean spaces, or for non-Euclidean geometry, are also known.
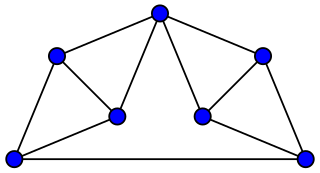
In graph theory, a branch of mathematics, the Moser spindle is an undirected graph, named after mathematicians Leo Moser and his brother William, with seven vertices and eleven edges. It is a unit distance graph requiring four colors in any graph coloring, and its existence can be used to prove that the chromatic number of the plane is at least four.
In graph theory, a branch of mathematics, a crown graph on 2n vertices is an undirected graph with two sets of vertices {u1, u2, …, un} and {v1, v2, …, vn} and with an edge from ui to vj whenever i ≠ j.
In graph theory, an area of mathematics, an equitable coloring is an assignment of colors to the vertices of an undirected graph, in such a way that
In graph theory, the De Bruijn–Erdős theorem relates graph coloring of an infinite graph to the same problem on its finite subgraphs. It states that, when all finite subgraphs can be colored with colors, the same is true for the whole graph. The theorem was proved by Nicolaas Govert de Bruijn and Paul Erdős, after whom it is named.

In combinatorial mathematics, the Albertson conjecture is an unproven relationship between the crossing number and the chromatic number of a graph. It is named after Michael O. Albertson, a professor at Smith College, who stated it as a conjecture in 2007; it is one of his many conjectures in graph coloring theory. The conjecture states that, among all graphs requiring colors, the complete graph is the one with the smallest crossing number. Equivalently, if a graph can be drawn with fewer crossings than , then, according to the conjecture, it may be colored with fewer than colors.
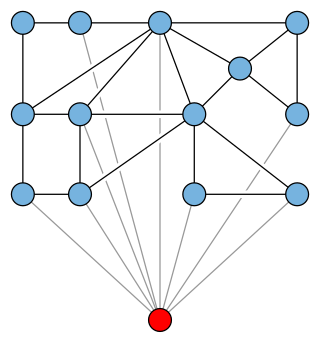
In graph theory, a branch of mathematics, an apex graph is a graph that can be made planar by the removal of a single vertex. The deleted vertex is called an apex of the graph. It is an apex, not the apex because an apex graph may have more than one apex; for example, in the minimal nonplanar graphs K5 or K3,3, every vertex is an apex. The apex graphs include graphs that are themselves planar, in which case again every vertex is an apex. The null graph is also counted as an apex graph even though it has no vertex to remove.

In mathematics, and particularly in graph theory, the dimension of a graph is the least integer n such that there exists a "classical representation" of the graph in the Euclidean space of dimension n with all the edges having unit length.

In graph theory, the Golomb graph is a polyhedral graph with 10 vertices and 18 edges. It is named after Solomon W. Golomb, who constructed it as a unit distance graph that requires four colors in any graph coloring. Thus, like the simpler Moser spindle, it provides a lower bound for the Hadwiger–Nelson problem: coloring the points of the Euclidean plane so that each unit line segment has differently-colored endpoints requires at least four colors.
The Mathematical Coloring Book: Mathematics of Coloring and the Colorful Life of Its Creators is a book on graph coloring, Ramsey theory, and the history of development of these areas, concentrating in particular on the Hadwiger–Nelson problem and on the biography of Bartel Leendert van der Waerden. It was written by Alexander Soifer and published by Springer-Verlag in 2009 (ISBN 978-0-387-74640-1).