Hard-core predicate

Last updated

In cryptography, a hard-core predicate of a one-way function f is a predicate b (i.e., a function whose output is a single bit) which is easy to compute (as a function of x) but is hard to compute given f(x). In formal terms, there is no probabilistic polynomial-time (PPT) algorithm that computes b(x) from f(x) with probability significantly greater than one half over random choice of x. [1] :34 In other words, if x is drawn uniformly at random, then given f(x), any PPT adversary can only distinguish the hard-core bit b(x) and a uniformly random bit with negligible advantage over the length of x. [2]

Cryptography practice and study of techniques for secure communication in the presence of third parties

Cryptography or cryptology is the practice and study of techniques for secure communication in the presence of third parties called adversaries. More generally, cryptography is about constructing and analyzing protocols that prevent third parties or the public from reading private messages; various aspects in information security such as data confidentiality, data integrity, authentication, and non-repudiation are central to modern cryptography. Modern cryptography exists at the intersection of the disciplines of mathematics, computer science, electrical engineering, communication science, and physics. Applications of cryptography include electronic commerce, chip-based payment cards, digital currencies, computer passwords, and military communications.

In computer science, a one-way function is a function that is easy to compute on every input, but hard to invert given the image of a random input. Here, "easy" and "hard" are to be understood in the sense of computational complexity theory, specifically the theory of polynomial time problems. Not being one-to-one is not considered sufficient of a function for it to be called one-way.

In cryptography, an adversary's advantage is a measure of how successfully it can attack a cryptographic algorithm, by distinguishing it from an idealized version of that type of algorithm. Note that in this context, the "adversary" is itself an algorithm and not a person. A cryptographic algorithm is considered secure if no adversary has a non-negligible advantage, subject to specified bounds on the adversary's computational resources. "Negligible" usually means "within O(2−p)" where p is a security parameter associated with the algorithm. For example, p might be the number of bits in a block cipher's key.

A hard-core function can be defined similarly. That is, if x is chosen uniformly at random, then given f(x), any PPT algorithm can only distinguish the hard-core function value h(x) and uniformly random bits of length |h(x)| with negligible advantage over the length of x. [3] [4]

A hard-core predicate captures "in a concentrated sense" the hardness of inverting f.

While a one-way function is hard to invert, there are no guarantees about the feasibility of computing partial information about the preimage c from the image f(x). For instance, while RSA is conjectured to be a one-way function, the Jacobi symbol of the preimage can be easily computed from that of the image. [1] :121

The Jacobi symbol is a generalization of the Legendre symbol. Introduced by Jacobi in 1837, it is of theoretical interest in modular arithmetic and other branches of number theory, but its main use is in computational number theory, especially primality testing and integer factorization; these in turn are important in cryptography.

It is clear that if a one-to-one function has a hard-core predicate, then it must be one way. Oded Goldreich and Leonid Levin (1989) showed how every one-way function can be trivially modified to obtain a one-way function that has a specific hard-core predicate. [5] Let f be a one-way function. Define g(x,r) = (f(x), r) where the length of r is the same as that of x. Let xj denote the jth bit of x and rj the jth bit of r. Then

Injective function

In mathematics, an injective function or injection or one-to-one function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is the image of at most one element of its domain. The term one-to-one function must not be confused with one-to-one correspondence, which uniquely maps all elements in both domain and codomain to each other.

Oded Goldreich Israeli cryptographer

Oded Goldreich is a professor of Computer Science at the Faculty of Mathematics and Computer Science of Weizmann Institute of Science, Israel. His research interests lie within the theory of computation and are, specifically, the interplay of randomness and computation, the foundations of cryptography, and computational complexity theory. He won the Knuth Prize in 2017.

Leonid Levin Russian mathematician

Leonid Anatolievich Levin is a Soviet-American computer scientist.

is a hard core predicate of g. Note that b(x, r) = <x, r> where <·, ·> denotes the standard inner product on the vector space (Z2)n. This predicate is hard-core due to computational issues; that is, it is not hard to compute because g(x, r) is information theoretically lossy. Rather, if there exists an algorithm that computes this predicate efficiently, then there is another algorithm that can invert f efficiently.

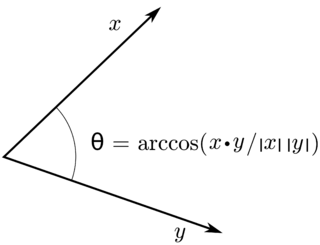
Inner product space vector space with an additional structure called an inner product

In linear algebra, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors. Inner products allow the rigorous introduction of intuitive geometrical notions such as the length of a vector or the angle between two vectors. They also provide the means of defining orthogonality between vectors. Inner product spaces generalize Euclidean spaces to vector spaces of any dimension, and are studied in functional analysis. The first usage of the concept of a vector space with an inner product is due to Giuseppe Peano, in 1898.

Vector space mathematical structure formed by a collection of elements called vectors

A vector space is a collection of objects called vectors, which may be added together and multiplied ("scaled") by numbers, called scalars. Scalars are often taken to be real numbers, but there are also vector spaces with scalar multiplication by complex numbers, rational numbers, or generally any field. The operations of vector addition and scalar multiplication must satisfy certain requirements, called axioms, listed below.

Information theory studies the quantification, storage, and communication of information. It was originally proposed by Claude Shannon in 1948 to find fundamental limits on signal processing and communication operations such as data compression, in a landmark paper entitled "A Mathematical Theory of Communication". Applications of fundamental topics of information theory include lossless data compression, lossy data compression, and channel coding. Its impact has been crucial to the success of the Voyager missions to deep space, the invention of the compact disc, the feasibility of mobile phones, the development of the Internet, the study of linguistics and of human perception, the understanding of black holes, and numerous other fields.

A similar construction yields a hard-core function with O(log |x|) output bits. Suppose f is a strong one-way function. Define g(x, r) = (f(x), r) where |r| = 2|x|. Choose a length function l(n) = O(log n) s.t. l(n) ≤ n. Let

Then h(x, r) := b1(x, r) b2(x, r) ... bl(|x|)(x, r) is a hard-core function with output length l(|x|). [6]

It is sometimes the case that an actual bit of the input x is hard-core. For example, every single bit of inputs to the RSA function is a hard-core predicate of RSA and blocks of O(log |x|) bits of x are indistinguishable from random bit strings in polynomial time (under the assumption that the RSA function is hard to invert). [7]

Hard-core predicates give a way to construct a pseudorandom generator from any one-way permutation. If b is a hard-core predicate of a one-way permutation f, and s is a random seed, then

is a pseudorandom bit sequence, where fn means the n-th iteration of applying f on s, and b is the generated hard-core bit by each round n. [1] :132

Hard-core predicates of trapdoor one-way permutations (known as trapdoor predicates) can be used to construct semantically secure public-key encryption schemes. [1] :129

See also

Related Research Articles

In cryptography, a block cipher is a deterministic algorithm operating on fixed-length groups of bits, called a block, with an unvarying transformation that is specified by a symmetric key. Block ciphers operate as important elementary components in the design of many cryptographic protocols, and are widely used to implement encryption of bulk data.

Hash function type of function that can be used to map data of arbitrary size to data of fixed size

A hash function is any function that can be used to map data of arbitrary size onto data of a fixed size. The values returned by a hash function are called hash values, hash codes, digests, or simply hashes. Hash functions are often used in combination with a hash table, a common data structure used in computer software for rapid data lookup. Hash functions accelerate table or database lookup by detecting duplicated records in a large file. One such application is finding similar stretches in DNA sequences. They are also useful in cryptography. A cryptographic hash function allows one to easily verify whether some input data map onto a given hash value, but if the input data is unknown it is deliberately difficult to reconstruct it by knowing the stored hash value. This is used for assuring integrity of transmitted data, and is the building block for HMACs, which provide message authentication.

RSA (Rivest–Shamir–Adleman) is one of the first public-key cryptosystems and is widely used for secure data transmission. In such a cryptosystem, the encryption key is public and it is different from the decryption key which is kept secret (private). In RSA, this asymmetry is based on the practical difficulty of the factorization of the product of two large prime numbers, the "factoring problem". The acronym RSA is made of the initial letters of the surnames of Ron Rivest, Adi Shamir, and Leonard Adleman, who first publicly described the algorithm in 1978. Clifford Cocks, an English mathematician working for the British intelligence agency Government Communications Headquarters (GCHQ), had developed an equivalent system in 1973, but this was not declassified until 1997.

A cryptographically secure pseudo-random number generator (CSPRNG) or cryptographic pseudo-random number generator (CPRNG) is a pseudo-random number generator (PRNG) with properties that make it suitable for use in cryptography.

Trapdoor function type of function that is easy to compute in one direction, yet difficult to compute in the opposite direction without special information

A trapdoor function is a function that is easy to compute in one direction, yet difficult to compute in the opposite direction without special information, called the "trapdoor". Trapdoor functions are widely used in cryptography.

A commitment scheme is a cryptographic primitive that allows one to commit to a chosen value while keeping it hidden to others, with the ability to reveal the committed value later. Commitment schemes are designed so that a party cannot change the value or statement after they have committed to it: that is, commitment schemes are binding. Commitment schemes have important applications in a number of cryptographic protocols including secure coin flipping, zero-knowledge proofs, and secure computation.

In cryptography, a random oracle is an oracle that responds to every unique query with a (truly) random response chosen uniformly from its output domain. If a query is repeated it responds the same way every time that query is submitted.

In cryptography, blinding is a technique by which an agent can provide a service to a client in an encoded form without knowing either the real input or the real output. Blinding techniques also have applications to preventing side-channel attacks on encryption devices.

In cryptography, the McEliece cryptosystem is an asymmetric encryption algorithm developed in 1978 by Robert McEliece. It was the first such scheme to use randomization in the encryption process. The algorithm has never gained much acceptance in the cryptographic community, but is a candidate for "post-quantum cryptography", as it is immune to attacks using Shor's algorithm and — more generally — measuring coset states using Fourier sampling.

Probabilistic encryption is the use of randomness in an encryption algorithm, so that when encrypting the same message several times it will, in general, yield different ciphertexts. The term "probabilistic encryption" is typically used in reference to public key encryption algorithms, however various symmetric key encryption algorithms achieve a similar property. To be semantically secure, that is, to hide even partial information about the plaintext, an encryption algorithm must be probabilistic.

In cryptography, Optimal Asymmetric Encryption Padding (OAEP) is a padding scheme often used together with RSA encryption. OAEP was introduced by Bellare and Rogaway, and subsequently standardized in PKCS#1 v2 and RFC 2437.

Random self-reducibility (RSR) is the rule that a good algorithm for the average case implies a good algorithm for the worst case. RSR is the ability to solve all instances of a problem by solving a large fraction of the instances.

In computational complexity theory and cryptography, the existence of pseudorandom generators is related to the existence of one-way functions through a number of theorems, collectively referred to as the pseudorandom generator theorem.

In computational complexity theory, the average-case complexity of an algorithm is the amount of some computational resource used by the algorithm, averaged over all possible inputs. It is frequently contrasted with worst-case complexity which considers the maximal complexity of the algorithm over all possible inputs.

SHA-3 is the latest member of the Secure Hash Algorithm family of standards, released by NIST on August 5, 2015. Although part of the same series of standards, SHA-3 is internally different from the MD5-like structure of SHA-1 and SHA-2.

Post-quantum cryptography refers to cryptographic algorithms that are thought to be secure against an attack by a quantum computer. As of 2018, this is not true for the most popular public-key algorithms, which can be efficiently broken by a sufficiently strong hypothetical quantum computer. The problem with currently popular algorithms is that their security relies on one of three hard mathematical problems: the integer factorization problem, the discrete logarithm problem or the elliptic-curve discrete logarithm problem. All of these problems can be easily solved on a sufficiently powerful quantum computer running Shor's algorithm. Even though current, publicly known, experimental quantum computers lack processing power to break any real cryptographic algorithm, many cryptographers are designing new algorithms to prepare for a time when quantum computing becomes a threat. This work has gained greater attention from academics and industry through the PQCrypto conference series since 2006 and more recently by several workshops on Quantum Safe Cryptography hosted by the European Telecommunications Standards Institute (ETSI) and the Institute for Quantum Computing.

VMPC is a stream cipher similar to the well known and popular cipher RC4 designed by Ron Rivest. It was designed by Bartosz Zoltak, presented in 2004 at the Fast Software Encryption conference. VMPC is a modification of the RC4 cipher.

References

  1. 1 2 3 4 Goldwasser, S. and Bellare, M. "Lecture Notes on Cryptography". Summer course on cryptography, MIT, 1996-2001
  2. ↑ Definition 2.4 in Lindell, Yehuda. "Foundations of Cryptography 89-856" (PDF). Computer Science, Bar Ilan University. Bar Ilan University. Retrieved 11 January 2016.
  3. ↑ Goldreich's FoC, vol 1, def 2.5.5.
  4. ↑ Definition 3 in Holenstein, Thomas; et al. "Complete Classification of Bilinear Hard-Core Functions" (PDF). IACR eprint. IACR. Retrieved 11 January 2016.
  5. ↑ O. Goldreich and L.A. Levin, A Hard-Core Predicate for all One-Way Functions, STOC 1989, pp25–32.
  6. ↑ Goldreich's FoC, vol 1, Theorem 2.5.6.
  7. ↑ J. Håstad, M. Naslund, The Security of all RSA and Discrete Log Bits (2004): Journal of the ACM, 2004.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.