
Fick's laws of diffusion describe diffusion and were first posited by Adolf Fick in 1855 on the basis of largely experimental results. They can be used to solve for the diffusion coefficient, D. Fick's first law can be used to derive his second law which in turn is identical to the diffusion equation.
In heat transfer analysis, thermal diffusivity is the thermal conductivity divided by density and specific heat capacity at constant pressure. It measures the rate of transfer of heat of a material from the hot end to the cold end. It has the SI derived unit of m2/s. Thermal diffusivity is usually denoted by lowercase alpha, but a, h, κ (kappa), K, and D are also used.

In mathematics and physics, the heat equation is a certain partial differential equation. Solutions of the heat equation are sometimes known as caloric functions. The theory of the heat equation was first developed by Joseph Fourier in 1822 for the purpose of modeling how a quantity such as heat diffuses through a given region.

In physics, the dynamo theory proposes a mechanism by which a celestial body such as Earth or a star generates a magnetic field. The dynamo theory describes the process through which a rotating, convecting, and electrically conducting fluid can maintain a magnetic field over astronomical time scales. A dynamo is thought to be the source of the Earth's magnetic field and the magnetic fields of Mercury and the Jovian planets.
A continuity equation or transport equation is an equation that describes the transport of some quantity. It is particularly simple and powerful when applied to a conserved quantity, but it can be generalized to apply to any extensive quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described using continuity equations.

In thermodynamics, the Onsager reciprocal relations express the equality of certain ratios between flows and forces in thermodynamic systems out of equilibrium, but where a notion of local equilibrium exists.

Electromigration is the transport of material caused by the gradual movement of the ions in a conductor due to the momentum transfer between conducting electrons and diffusing metal atoms. The effect is important in applications where high direct current densities are used, such as in microelectronics and related structures. As the structure size in electronics such as integrated circuits (ICs) decreases, the practical significance of this effect increases.
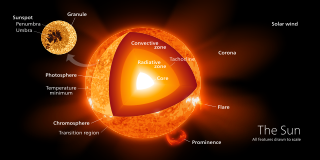
A radiation zone, or radiative region is a layer of a star's interior where energy is primarily transported toward the exterior by means of radiative diffusion and thermal conduction, rather than by convection. Energy travels through the radiation zone in the form of electromagnetic radiation as photons.
In physics, the Einstein relation is a previously unexpected connection revealed independently by William Sutherland in 1904, Albert Einstein in 1905, and by Marian Smoluchowski in 1906 in their works on Brownian motion. The more general form of the equation in the classical case is

Opacity is the measure of impenetrability to electromagnetic or other kinds of radiation, especially visible light. In radiative transfer, it describes the absorption and scattering of radiation in a medium, such as a plasma, dielectric, shielding material, glass, etc. An opaque object is neither transparent nor translucent. When light strikes an interface between two substances, in general some may be reflected, some absorbed, some scattered, and the rest transmitted. Reflection can be diffuse, for example light reflecting off a white wall, or specular, for example light reflecting off a mirror. An opaque substance transmits no light, and therefore reflects, scatters, or absorbs all of it. Other categories of visual appearance, related to the perception of regular or diffuse reflection and transmission of light, have been organized under the concept of cesia in an order system with three variables, including opacity, transparency and translucency among the involved aspects. Both mirrors and carbon black are opaque. Opacity depends on the frequency of the light being considered. For instance, some kinds of glass, while transparent in the visual range, are largely opaque to ultraviolet light. More extreme frequency-dependence is visible in the absorption lines of cold gases. Opacity can be quantified in many ways; for example, see the article mathematical descriptions of opacity.

The lattice Boltzmann methods (LBM), originated from the lattice gas automata (LGA) method (Hardy-Pomeau-Pazzis and Frisch-Hasslacher-Pomeau models), is a class of computational fluid dynamics (CFD) methods for fluid simulation. Instead of solving the Navier–Stokes equations directly, a fluid density on a lattice is simulated with streaming and collision (relaxation) processes. The method is versatile as the model fluid can straightforwardly be made to mimic common fluid behaviour like vapour/liquid coexistence, and so fluid systems such as liquid droplets can be simulated. Also, fluids in complex environments such as porous media can be straightforwardly simulated, whereas with complex boundaries other CFD methods can be hard to work with.
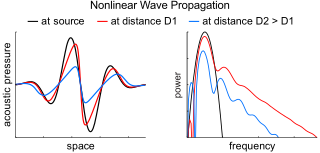
Nonlinear acoustics (NLA) is a branch of physics and acoustics dealing with sound waves of sufficiently large amplitudes. Large amplitudes require using full systems of governing equations of fluid dynamics and elasticity. These equations are generally nonlinear, and their traditional linearization is no longer possible. The solutions of these equations show that, due to the effects of nonlinearity, sound waves are being distorted as they travel.

HydroGeoSphere (HGS) is a 3D control-volume finite element groundwater model, and is based on a rigorous conceptualization of the hydrologic system consisting of surface and subsurface flow regimes. The model is designed to take into account all key components of the hydrologic cycle. For each time step, the model solves surface and subsurface flow, solute and energy transport equations simultaneously, and provides a complete water and solute balance.
The convection–diffusion equation is a combination of the diffusion and convection (advection) equations, and describes physical phenomena where particles, energy, or other physical quantities are transferred inside a physical system due to two processes: diffusion and convection. Depending on context, the same equation can be called the advection–diffusion equation, drift–diffusion equation, or (generic) scalar transport equation.

Diffusion is the net movement of anything generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. In the context of Quantum Physics, diffusion refers to spreading of wave packets. In simplest example, a Gaussian wave packet will spread along the spatial dimensions, as time progresses, resulting in diffusion of the wave packet energy. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, like in spinodal decomposition. Diffusion is a stochastic process due to the inherent randomness of the diffusing entity and can be used to model many real-life stochastic scenarios. Therefore, diffusion and the corresponding mathematical models are used in several fields, beyond physics, such as statistics, probability theory, information theory, neural networks, finance and marketing etc.
Relativistic heat conduction refers to the modelling of heat conduction in a way compatible with special relativity. In special relativity, the usual heat equation for non-relativistic heat conduction must be modified, as it leads to faster-than-light signal propagation. Relativistic heat conduction, therefore, encompasses a set of models for heat propagation in continuous media that are consistent with relativistic causality, namely the principle that an effect must be within the light-cone associated to its cause. Any reasonable relativistic model for heat conduction must also be stable, in the sense that differences in temperature propagate both slower than light and are damped over time.
Miniaturizing components has always been a primary goal in the semiconductor industry because it cuts production cost and lets companies build smaller computers and other devices. Miniaturization, however, has increased dissipated power per unit area and made it a key limiting factor in integrated circuit performance. Temperature increase becomes relevant for relatively small-cross-sections wires, where it may affect normal semiconductor behavior. Besides, since the generation of heat is proportional to the frequency of operation for switching circuits, fast computers have larger heat generation than slow ones, an undesired effect for chips manufacturers. This article summaries physical concepts that describe the generation and conduction of heat in an integrated circuit, and presents numerical methods that model heat transfer from a macroscopic point of view.

Double diffusive convection is a fluid dynamics phenomenon that describes a form of convection driven by two different density gradients, which have different rates of diffusion.
The porous medium equation, also called the nonlinear heat equation, is a nonlinear partial differential equation taking the form:
In fluid dynamics, the general equation of heat transfer is a nonlinear partial differential equation describing specific entropy production in a Newtonian fluid subject to thermal conduction and viscous forces:

















