Hill–Beck land division problem

Last updated August 17, 2024

The following variant of the fair cake-cutting problem was introduced by Ted Hill in 1983.^[1]

There is a territory D adjacent to n countries. Each country values the different subsets of D differently. The countries would like to divide D fairly among them, where "fair" means a proportional division. Additionally, the share allocated to each country must be connected and adjacent to that country. This geographic constraint distinguishes this problem from classic fair cake-cutting.

Formally, every country C_i must receive a disjoint piece of D, marked D_i, such that a portion of the border between C_i and D is contained in the interior of C_i ∪ D_i.

Impossibility and possibility

There are cases in which the problem cannot be solved:

If there is a single point to which two countries assign all their value (e.g. a holy place), then obviously the territory cannot be divided proportionally. To prevent such situations, we assume that all countries assign a value of 0 to all singular points.
If D is a square, there are 4 countries adjacent to the 4 sides of the square, and each country assigns all its value to the border at the opposite side, then every allocation that connects, say, the northern country with its desired southern border will make it impossible to connect the eastern country with its desired western border (as long as we are in a two-dimensional plane). To prevent such situations, we assume that all countries assign a value of 0 to the boundary of D.

In 1983, Hill proved that, if each single point in D has a value of 0 for all countries, and the boundary of D has a value of 0 for all countries, then there exists a proportional division with the adjacency constraint. His proof was only existential – no algorithm was described.^[1]

Algorithm

4 years later, Anatole Beck described a protocol for attaining such a division.^[2] In essence, the protocol is an elaboration of the Last diminisher protocol. It lets the countries bid for parts of D, gives the smallest bid to its bidder and divides the remainder among the remaining n − 1 countries. Some variations are needed to guarantee that the adjacency constraint is satisfied.

Simply-connected territory

When D is simply-connected, the following algorithm is used.

1. Find a Riemann mapping h that maps D to the unit disc, such that for all countries, the value of every circle centered at the origin is 0 and the value of every radius from the origin is 0 (the existence of such an h is proved by a counting argument).

2. Ask each country to draw, on the unit disc map h(D), a disc centered at the origin with a value of 1/n. This is possible thanks to the condition that the value of all circles centered at the origin is 0.

3. Find the disc D₁ with the smallest radius, r₁.

There are two cases.

Single winner

4. If D₁ was drawn by only a single country, say C_i, then give this disc to C_i. Its value for the other countries is strictly less than 1/n, so we can give to C_i a small additional piece connecting it to its allocated disc.

To do this, draw a sector connecting D₁ to the image of the boundary between C_i and D. Let each country (other than C_i) trim this sector such that all countries value the union of the disc and the sector as at most 1/n. This is possible thanks to the condition that the value of all radii from the origin is 0. Allocate to C_i the union of D₁ and the trimmed sector.

The remainder is simply-connected and has a value of at least (n − 1)/n to the remaining n − 1 countries, so the division can proceed recursively in step 1.

Many winners

If D₁ was drawn by k>1 countries, then some more sophisticated auctions are required in order to find a country to which we can give a disc and a connecting sector.

5. pick an arbitrary winner country and call it the declarer, C₁. Let it add a sector connecting D₁ to its current territory, and let the other countries trim that sector such that:

For every non-winning country, the value of D₁ plus the trimmed sector is at most 1/n (this is possible because the value of D₁ for them is less than 1/n).
For every winning country, the value of the trimmed sector alone is less than 1/n.

6. Let each of the winning countries bid a new radius r (smaller than its first bid), such that the value of the trimmed sector plus the disc of radius r is exactly 1/n. Select the smallest such disc, D₂. Again there are two cases:

If C₁ is one of the countries bidding D₂, then just give it D₂ (which is slightly smaller than the original D₁) and the connecting sector. C₁ agreed that the value is 1/n and the other countries agreed that it is at most 1/n, so we can proceed recursively at step 1.

Otherwise, C₁ agrees that the total value of D₂ plus the connecting sector is less than 1/n. All non-winners must also agree to this since D₂ is smaller than D₁. So C₁ and all other countries that agree to this are removed from the set of winners.

7. From among the remaining winners, pick a new declarer C₂. Let it add another sector connecting D₂ to its current territory, and let the other countries trim that sector as in step 5.

Note that now D₂ is connected to two different territories – C₁ and C₂. This is a problem because it makes the remaining territory disconnected. To solve this, C₂ is allowed to take another sector, this time of length less than 1 so that it doesn't harm the connectivity.^[2] That third sector is again trimmed by all countries as in step 5. In return, C₂ is required to give up some part of the sector connecting D₂ to C₁, whose value is equal to the value of the third sector it received.

C₂'s candidate allocation now contains the following parts: D₂, a single sector of length 1 connecting D₂ to C₂, and two short sectors that do not reach the border of D. The value of this construction for C₂ is 1/n, its value for the non-winners is less than 1/n, and its value for the remaining winners is at most 1/n.

This process continues with the remaining winners, until only a single winner remains.

Finitely-connected territory

If the territory D is k-connected with a finite k, then the division can proceed by induction on k.

When k = 1, D is simply-connected and can be divided by the protocol of the previous section.

Otherwise (k > 1), mark the outer boundary of D by B₁ and its inner boundaries by B₂, ..., B_k.

Find a line L connecting the outer boundary B₁ to the inner boundary B_k, such that all countries value L as 0. This is possible by the following counting argument. There is an uncountable infinity of pairwise-disjoint lines connecting B₁ and B_k and contained in D. But the measure of D is finite, so the number of lines with a positive measure must be finite.

The set D \ L is (k − 1)-connected. Divide it recursively, then assign L arbitrarily to any country adjacent to it. This does not affect the fairness of the allocation since the value of L is 0 for all countries.

Related Research Articles

<span class="mw-page-title-main">Circle</span> Simple curve of Euclidean geometry

A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. The distance between any point of the circle and the centre is called the radius.

A multivibrator is an electronic circuit used to implement a variety of simple two-state devices such as relaxation oscillators, timers, latches and flip-flops. The first multivibrator circuit, the astable multivibrator oscillator, was invented by Henri Abraham and Eugene Bloch during World War I. It consisted of two vacuum tube amplifiers cross-coupled by a resistor-capacitor network. They called their circuit a "multivibrator" because its output waveform was rich in harmonics. A variety of active devices can be used to implement multivibrators that produce similar harmonic-rich wave forms; these include transistors, neon lamps, tunnel diodes and others. Although cross-coupled devices are a common form, single-element multivibrator oscillators are also common.

In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the ambient space which takes the object to itself, and which preserves all the relevant structure of the object. A frequent notation for the symmetry group of an object X is G = Sym(X).

In the mathematical field of differential geometry, the Gauss–Bonnet theorem is a fundamental formula which links the curvature of a surface to its underlying topology.

In geometry, the kissing number of a mathematical space is defined as the greatest number of non-overlapping unit spheres that can be arranged in that space such that they each touch a common unit sphere. For a given sphere packing in a given space, a kissing number can also be defined for each individual sphere as the number of spheres it touches. For a lattice packing the kissing number is the same for every sphere, but for an arbitrary sphere packing the kissing number may vary from one sphere to another.

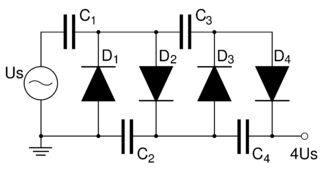
A voltage multiplier is an electrical circuit that converts AC electrical power from a lower voltage to a higher DC voltage, typically using a network of capacitors and diodes.

In mathematics, an Apollonian gasket or Apollonian net is a fractal generated by starting with a triple of circles, each tangent to the other two, and successively filling in more circles, each tangent to another three. It is named after Greek mathematician Apollonius of Perga.

In mathematics, and in particular in combinatorics, the combinatorial number system of degree k, also referred to as combinadics, or the Macaulay representation of an integer, is a correspondence between natural numbers N and k-combinations. The combinations are represented as strictly decreasing sequences c_k > ... > c₂ > c₁ ≥ 0 where each c_i corresponds to the index of a chosen element in a given k-combination. Distinct numbers correspond to distinct k-combinations, and produce them in lexicographic order. The numbers less than $correspond to all k -combinations of {0, 1, ..., n - 1}. The correspondence does not depend on the size n of the set that the k -combinations are taken from, so it can be interpreted as a map from N to the k -combinations taken from N; in this view the correspondence is a bijection.$

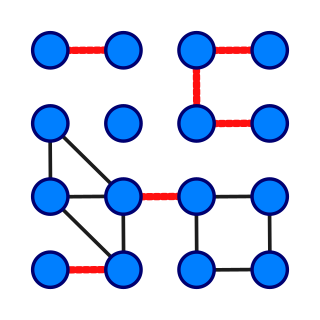
In graph theory, a bridge, isthmus, cut-edge, or cut arc is an edge of a graph whose deletion increases the graph's number of connected components. Equivalently, an edge is a bridge if and only if it is not contained in any cycle. For a connected graph, a bridge can uniquely determine a cut. A graph is said to be bridgeless or isthmus-free if it contains no bridges.

The Cockcroft–Walton (CW) generator, or multiplier, is an electric circuit that generates a high DC voltage from a low-voltage AC. It was named after the British and Irish physicists John Douglas Cockcroft and Ernest Thomas Sinton Walton, who in 1932 used this circuit design to power their particle accelerator, performing the first artificial nuclear disintegration in history. They used this voltage multiplier cascade for most of their research, which in 1951 won them the Nobel Prize in Physics for "Transmutation of atomic nuclei by artificially accelerated atomic particles".

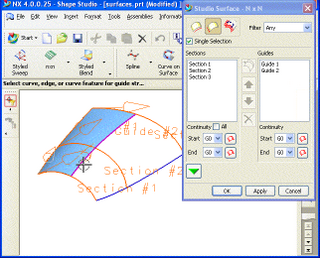
Freeform surface modelling is a technique for engineering freeform surfaces with a CAD or CAID system.

In geometry, a two-dimensional point group or rosette group is a group of geometric symmetries (isometries) that keep at least one point fixed in a plane. Every such group is a subgroup of the orthogonal group O(2), including O(2) itself. Its elements are rotations and reflections, and every such group containing only rotations is a subgroup of the special orthogonal group SO(2), including SO(2) itself. That group is isomorphic to R/Z and the first unitary group, U(1), a group also known as the circle group.

In hyperbolic geometry, a hypercycle, hypercircle or equidistant curve is a curve whose points have the same orthogonal distance from a given straight line.

<i>Catene</i> (album) 1984 studio album by Mina

Catene is a double studio album by Italian singer Mina, released in October 1983 by PDU and distributed by EMI Italiana.

The FIBA World Olympic Qualifying Tournament for Men 2008 was the final qualifying tournament for the 2008 Olympic men's basketball tournament. Organized by FIBA, it took place from 14 to 20 July 2008 at the OAKA Indoor Sports Arena, in Athens, Greece. The draw for the tournament was held on 31 January 2008 at the Divani Caravel hotel in Athens.

<i>Kyrie</i> (album) 1980 studio album by Mina

Kyrie is a double studio album by Italian singer Mina released on 27 November 1980 by PDU and distributed by EMI Italiana. Later the album was released in separate parts with subtitles "Vol. 1" and "Vol. 2". On this album Mina experiments with various genres, especially rock. The cover of the album features Mina's son Massimiliano Pani dressed as a hockey player.

The Kawasaki KR-1 and KR-1S are road-orientated 249 cc (15.2 cu in) two-stroke sports bikes introduced between 1988 and 1992 by Kawasaki Heavy Industries.

The 2012 FIBA World Olympic Qualifying Tournament was a men's basketball tournament that consisted of 12 national teams, where the top three teams earned a place in the 2012 Olympics basketball tournament. It was held on 2–8 July 2012 in Caracas, Venezuela.

In statistics and data analysis, the application software SegReg is a free and user-friendly tool for linear segmented regression analysis to determine the breakpoint where the relation between the dependent variable and the independent variable changes abruptly.

<i>Italiana</i> (album) 1982 studio album by Mina

Italiana is a double studio album by Italian singer Mina, released in November 1982 by PDU and distributed by EMI Italiana.

References

1 2 Hill, T. P. (1983). "Determining a Fair Border". The American Mathematical Monthly. 90 (7): 438–442. doi:10.2307/2975720. JSTOR 2975720.
1 2 Beck, A. (1987). "Constructing a Fair Border". The American Mathematical Monthly. 94 (2): 157–162. doi:10.2307/2322417. JSTOR 2322417.

For an additional solution to the problem, see: Webb, W. A. (1990). "A Combinatorial Algorithm to Establish a Fair Border". European Journal of Combinatorics. 11 (3): 301–304. doi:10.1016/s0195-6698(13)80129-1.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[Hill-1] 1 2 Hill, T. P. (1983). "Determining a Fair Border". The American Mathematical Monthly. 90 (7): 438–442. doi:10.2307/2975720. JSTOR 2975720.

[Beck-2] 1 2 Beck, A. (1987). "Constructing a Fair Border". The American Mathematical Monthly. 94 (2): 157–162. doi:10.2307/2322417. JSTOR 2322417.

[1]

[2]