The honeycomb conjecture states that a regular hexagonal grid or honeycomb has the least total perimeter of any subdivision of the plane into regions of equal area. The conjecture was proven in 1999 by mathematician Thomas C. Hales. [1]
The honeycomb conjecture states that a regular hexagonal grid or honeycomb has the least total perimeter of any subdivision of the plane into regions of equal area. The conjecture was proven in 1999 by mathematician Thomas C. Hales. [1]
Let be any system of smooth curves in , subdividing the plane into regions (connected components of the complement of ) all of which are bounded and have unit area. Then, averaged over large disks in the plane, the average length of per unit area is at least as large as for the hexagon tiling. The theorem applies even if the complement of has additional components that are unbounded or whose area is not one; allowing these additional components cannot shorten . Formally, let denote the disk of radius centered at the origin, let denote the total length of , and let denote the total area of covered by bounded unit-area components. (If these are the only components, then .) Then the theorem states that The value on the right hand side of the inequality is the limiting length per unit area of the hexagonal tiling.
The first record of the conjecture dates back to 36 BC, from Marcus Terentius Varro, but is often attributed to Pappus of Alexandria (c. 290 – c. 350). [2] In the 17th century, Jan Brożek used a similar theorem to argue why bees create hexagonal honeycombs. In 1943, László Fejes Tóth published a proof for a special case of the conjecture, in which each cell is required to be a convex polygon. [3] The full conjecture was proven in 1999 by mathematician Thomas C. Hales, who mentions in his work that there is reason to believe that the conjecture may have been present in the minds of mathematicians before Varro. [1] [2]
It is also related to the densest circle packing of the plane, in which every circle is tangent to six other circles, which fill just over 90% of the area of the plane.
The case when the problem is restricted to a square grid was solved in 1989 by Jaigyoung Choe who proved that the optimal figure is an irregular hexagon. [4] [5]
In mathematics, curvature is any of several strongly related concepts in geometry that intuitively measure the amount by which a curve deviates from being a straight line or by which a surface deviates from being a plane. If a curve or surface is contained in a larger space, curvature can be defined extrinsically relative to the ambient space. Curvature of Riemannian manifolds of dimension at least two can be defined intrinsically without reference to a larger space.
In mathematics, the Cauchy integral theorem in complex analysis, named after Augustin-Louis Cauchy, is an important statement about line integrals for holomorphic functions in the complex plane. Essentially, it says that if is holomorphic in a simply connected domain Ω, then for any simply closed contour in Ω, that contour integral is zero.
In mathematics, the winding number or winding index of a closed curve in the plane around a given point is an integer representing the total number of times that the curve travels counterclockwise around the point, i.e., the curve's number of turns. For certain open plane curves, the number of turns may be a non-integer. The winding number depends on the orientation of the curve, and it is negative if the curve travels around the point clockwise.
In trigonometry, the law of sines, sine law, sine formula, or sine rule is an equation relating the lengths of the sides of any triangle to the sines of its angles. According to the law, where a, b, and c are the lengths of the sides of a triangle, and α, β, and γ are the opposite angles, while R is the radius of the triangle's circumcircle. When the last part of the equation is not used, the law is sometimes stated using the reciprocals; The law of sines can be used to compute the remaining sides of a triangle when two angles and a side are known—a technique known as triangulation. It can also be used when two sides and one of the non-enclosed angles are known. In some such cases, the triangle is not uniquely determined by this data and the technique gives two possible values for the enclosed angle.
In vector calculus, Green's theorem relates a line integral around a simple closed curve C to a double integral over the plane region D bounded by C. It is the two-dimensional special case of Stokes' theorem. In one dimension, it is equivalent to the fundamental theorem of calculus. In three dimensions, it is equivalent to the divergence theorem.
In mathematics, the isoperimetric inequality is a geometric inequality involving the perimeter of a set and its volume. In -dimensional space the inequality lower bounds the surface area or perimeter of a set by its volume ,
The Kepler conjecture, named after the 17th-century mathematician and astronomer Johannes Kepler, is a mathematical theorem about sphere packing in three-dimensional Euclidean space. It states that no arrangement of equally sized spheres filling space has a greater average density than that of the cubic close packing and hexagonal close packing arrangements. The density of these arrangements is around 74.05%.
In the mathematical discipline of complex analysis, the analytic capacity of a compact subset K of the complex plane is a number that denotes "how big" a bounded analytic function on C \ K can become. Roughly speaking, γ(K) measures the size of the unit ball of the space of bounded analytic functions outside K.
In geometry, close-packing of equal spheres is a dense arrangement of congruent spheres in an infinite, regular arrangement. Carl Friedrich Gauss proved that the highest average density – that is, the greatest fraction of space occupied by spheres – that can be achieved by a lattice packing is
In Euclidean geometry, Ptolemy's theorem is a relation between the four sides and two diagonals of a cyclic quadrilateral. The theorem is named after the Greek astronomer and mathematician Ptolemy. Ptolemy used the theorem as an aid to creating his table of chords, a trigonometric table that he applied to astronomy.
In mathematics, Carathéodory's theorem is a theorem in complex analysis, named after Constantin Carathéodory, which extends the Riemann mapping theorem. The theorem, published by Carathéodory in 1913, states that any conformal mapping sending the unit disk to some region in the complex plane bounded by a Jordan curve extends continuously to a homeomorphism from the unit circle onto the Jordan curve. The result is one of Carathéodory's results on prime ends and the boundary behaviour of univalent holomorphic functions.
László Fejes Tóth was a Hungarian mathematician who specialized in geometry. He proved that a lattice pattern is the most efficient way to pack centrally symmetric convex sets on the Euclidean plane. He also investigated the sphere packing problem. He was the first to show, in 1953, that proof of the Kepler conjecture can be reduced to a finite case analysis and, later, that the problem might be solved using a computer.
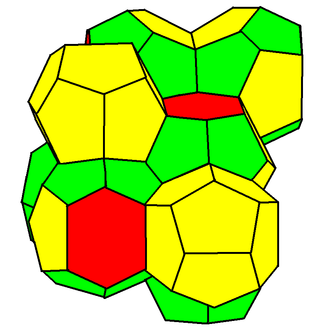
In geometry, the Weaire–Phelan structure is a three-dimensional structure representing an idealised foam of equal-sized bubbles, with two different shapes. In 1993, Denis Weaire and Robert Phelan found that this structure was a better solution of the Kelvin problem of tiling space by equal volume cells of minimum surface area than the previous best-known solution, the Kelvin structure.
In probability theory, the Schramm–Loewner evolution with parameter κ, also known as stochastic Loewner evolution (SLEκ), is a family of random planar curves that have been proven to be the scaling limit of a variety of two-dimensional lattice models in statistical mechanics. Given a parameter κ and a domain in the complex plane U, it gives a family of random curves in U, with κ controlling how much the curve turns. There are two main variants of SLE, chordal SLE which gives a family of random curves from two fixed boundary points, and radial SLE, which gives a family of random curves from a fixed boundary point to a fixed interior point. These curves are defined to satisfy conformal invariance and a domain Markov property.
In mathematics, specifically in operator K-theory, the Baum–Connes conjecture suggests a link between the K-theory of the reduced C*-algebra of a group and the K-homology of the classifying space of proper actions of that group. The conjecture sets up a correspondence between different areas of mathematics, with the K-homology of the classifying space being related to geometry, differential operator theory, and homotopy theory, while the K-theory of the group's reduced C*-algebra is a purely analytical object.
In complex analysis, a branch of mathematics, Bloch's theorem describes the behaviour of holomorphic functions defined on the unit disk. It gives a lower bound on the size of a disk in which an inverse to a holomorphic function exists. It is named after André Bloch.
In mathematics, the differential geometry of surfaces deals with the differential geometry of smooth surfaces with various additional structures, most often, a Riemannian metric.
In the mathematical theory of conformal mappings, the area theorem gives an inequality satisfied by the power series coefficients of certain conformal mappings. The theorem is called by that name, not because of its implications, but rather because the proof uses the notion of area.
In geometry, circle packing is the study of the arrangement of circles on a given surface such that no overlapping occurs and so that no circle can be enlarged without creating an overlap. The associated packing density, η, of an arrangement is the proportion of the surface covered by the circles. Generalisations can be made to higher dimensions – this is called sphere packing, which usually deals only with identical spheres.
In mathematics, the connective constant is a numerical quantity associated with self-avoiding walks on a lattice. It is studied in connection with the notion of universality in two-dimensional statistical physics models. While the connective constant depends on the choice of lattice so itself is not universal, it is nonetheless an important quantity that appears in conjectures for universal laws. Furthermore, the mathematical techniques used to understand the connective constant, for example in the recent rigorous proof by Duminil-Copin and Smirnov that the connective constant of the hexagonal lattice has the precise value , may provide clues to a possible approach for attacking other important open problems in the study of self-avoiding walks, notably the conjecture that self-avoiding walks converge in the scaling limit to the Schramm–Loewner evolution.
