
The Navier–Stokes equations are partial differential equations which describe the motion of viscous fluid substances. They were named after French engineer and physicist Claude-Louis Navier and the Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes).

In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function where U is an open subset of that satisfies Laplace's equation, that is,

In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is invertible, or equivalently that there are no real characteristic directions.
In physics, the Hamilton–Jacobi equation, named after William Rowan Hamilton and Carl Gustav Jacob Jacobi, is an alternative formulation of classical mechanics, equivalent to other formulations such as Newton's laws of motion, Lagrangian mechanics and Hamiltonian mechanics.
In the mathematical fields of differential equations and geometric analysis, the maximum principle is one of the most useful and best known tools of study. Solutions of a differential inequality in a domain D satisfy the maximum principle if they achieve their maxima at the boundary of D.
In mathematics, a hyperbolic partial differential equation of order is a partial differential equation (PDE) that, roughly speaking, has a well-posed initial value problem for the first derivatives. More precisely, the Cauchy problem can be locally solved for arbitrary initial data along any non-characteristic hypersurface. Many of the equations of mechanics are hyperbolic, and so the study of hyperbolic equations is of substantial contemporary interest. The model hyperbolic equation is the wave equation. In one spatial dimension, this is
In mathematics, the viscosity solution concept was introduced in the early 1980s by Pierre-Louis Lions and Michael G. Crandall as a generalization of the classical concept of what is meant by a 'solution' to a partial differential equation (PDE). It has been found that the viscosity solution is the natural solution concept to use in many applications of PDE's, including for example first order equations arising in dynamic programming, differential games or front evolution problems, as well as second-order equations such as the ones arising in stochastic optimal control or stochastic differential games.
In mathematics, Harnack's inequality is an inequality relating the values of a positive harmonic function at two points, introduced by A. Harnack. Harnack's inequality is used to prove Harnack's theorem about the convergence of sequences of harmonic functions. J. Serrin, and J. Moser generalized Harnack's inequality to solutions of elliptic or parabolic partial differential equations. Such results can be used to show the interior regularity of weak solutions.
In mathematics, a real or complex-valued function f on d-dimensional Euclidean space satisfies a Hölder condition, or is Hölder continuous, when there are real constants C ≥ 0, > 0, such that

The Navier–Stokes existence and smoothness problem concerns the mathematical properties of solutions to the Navier–Stokes equations, a system of partial differential equations that describe the motion of a fluid in space. Solutions to the Navier–Stokes equations are used in many practical applications. However, theoretical understanding of the solutions to these equations is incomplete. In particular, solutions of the Navier–Stokes equations often include turbulence, which remains one of the greatest unsolved problems in physics, despite its immense importance in science and engineering.
In mathematics, Gårding's inequality is a result that gives a lower bound for the bilinear form induced by a real linear elliptic partial differential operator. The inequality is named after Lars Gårding.

In mathematics, an elliptic boundary value problem is a special kind of boundary value problem which can be thought of as the stable state of an evolution problem. For example, the Dirichlet problem for the Laplacian gives the eventual distribution of heat in a room several hours after the heating is turned on.
The Hopf maximum principle is a maximum principle in the theory of second order elliptic partial differential equations and has been described as the "classic and bedrock result" of that theory. Generalizing the maximum principle for harmonic functions which was already known to Gauss in 1839, Eberhard Hopf proved in 1927 that if a function satisfies a second order partial differential inequality of a certain kind in a domain of Rn and attains a maximum in the domain then the function is constant. The simple idea behind Hopf's proof, the comparison technique he introduced for this purpose, has led to an enormous range of important applications and generalizations.
In the finite element method for the numerical solution of elliptic partial differential equations, the stiffness matrix is a matrix that represents the system of linear equations that must be solved in order to ascertain an approximate solution to the differential equation.
In mathematics, and more precisely, in functional Analysis and PDEs, the Schauder estimates are a collection of results due to Juliusz Schauder concerning the regularity of solutions to linear, uniformly elliptic partial differential equations. The estimates say that when the equation has appropriately smooth terms and appropriately smooth solutions, then the Hölder norm of the solution can be controlled in terms of the Hölder norms for the coefficient and source terms. Since these estimates assume by hypothesis the existence of a solution, they are called a priori estimates.
In mathematics, a free boundary problem is a partial differential equation to be solved for both an unknown function and an unknown domain . The segment of the boundary of which is not known at the outset of the problem is the free boundary.
In mathematics, Sobolev spaces for planar domains are one of the principal techniques used in the theory of partial differential equations for solving the Dirichlet and Neumann boundary value problems for the Laplacian in a bounded domain in the plane with smooth boundary. The methods use the theory of bounded operators on Hilbert space. They can be used to deduce regularity properties of solutions and to solve the corresponding eigenvalue problems.
The Leray projection, named after Jean Leray, is a linear operator used in the theory of partial differential equations, specifically in the fields of fluid dynamics. Informally, it can be seen as the projection on the divergence-free vector fields. It is used in particular to eliminate both the pressure term and the divergence-free term in the Stokes equations and Navier–Stokes equations.
In fluid dynamics, Rayleigh problem also known as Stokes first problem is a problem of determining the flow created by a sudden movement of an infinitely long plate from rest, named after Lord Rayleigh and Sir George Stokes. This is considered as one of the simplest unsteady problems that have an exact solution for the Navier-Stokes equations. The impulse movement of semi-infinite plate was studied by Keith Stewartson.
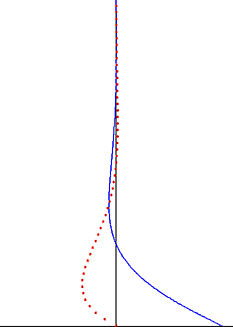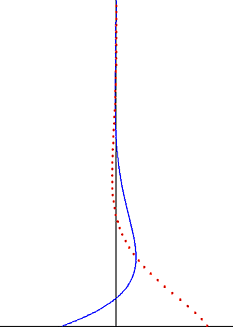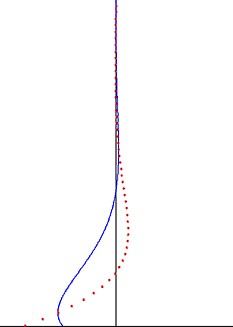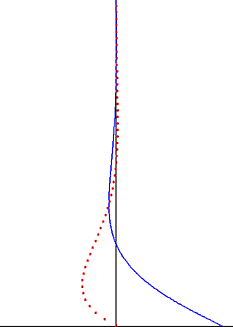
In fluid dynamics, Stokes problem also known as Stokes second problem or sometimes referred to as Stokes boundary layer or Oscillating boundary layer is a problem of determining the flow created by an oscillating solid surface, named after Sir George Stokes. This is considered one of the simplest unsteady problems that has an exact solution for the Navier–Stokes equations. In turbulent flow, this is still named a Stokes boundary layer, but now one has to rely on experiments, numerical simulations or approximate methods in order to obtain useful information on the flow.


































