
Bessel functions, first defined by the mathematician Daniel Bernoulli and then generalized by Friedrich Bessel, are canonical solutions y(x) of Bessel's differential equation

The Navier–Stokes equations are partial differential equations which describe the motion of viscous fluid substances. They were named after French engineer and physicist Claude-Louis Navier and the Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes).

In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points (cos t, sin t) form a circle with a unit radius, the points (cosh t, sinh t) form the right half of the unit hyperbola. Also, similarly to how the derivatives of sin(t) and cos(t) are cos(t) and –sin(t) respectively, the derivatives of sinh(t) and cosh(t) are cosh(t) and +sinh(t) respectively.

In mathematics, the beta function, also called the Euler integral of the first kind, is a special function that is closely related to the gamma function and to binomial coefficients. It is defined by the integral

In mathematics, the Gudermannian function relates a hyperbolic angle measure to a circular angle measure called the gudermannian of and denoted . The Gudermannian function reveals a close relationship between the circular functions and hyperbolic functions. It was introduced in the 1760s by Johann Heinrich Lambert, and later named for Christoph Gudermann who also described the relationship between circular and hyperbolic functions in 1830. The gudermannian is sometimes called the hyperbolic amplitude as a limiting case of the Jacobi elliptic amplitude when parameter

In geometry, a solid of revolution is a solid figure obtained by rotating a plane figure around some straight line, which may not intersect the generatrix. The surface created by this revolution and which bounds the solid is the surface of revolution.

In the physical sciences, the Airy function (or Airy function of the first kind) Ai(x) is a special function named after the British astronomer George Biddell Airy (1801–1892). The function Ai(x) and the related function Bi(x), are linearly independent solutions to the differential equation
In the mathematical field of complex analysis, contour integration is a method of evaluating certain integrals along paths in the complex plane.

In geometry, hyperbolic angle is a real number determined by the area of the corresponding hyperbolic sector of xy = 1 in Quadrant I of the Cartesian plane. The hyperbolic angle parametrises the unit hyperbola, which has hyperbolic functions as coordinates. In mathematics, hyperbolic angle is an invariant measure as it is preserved under hyperbolic rotation.
In calculus, the Leibniz integral rule for differentiation under the integral sign states that for an integral of the form
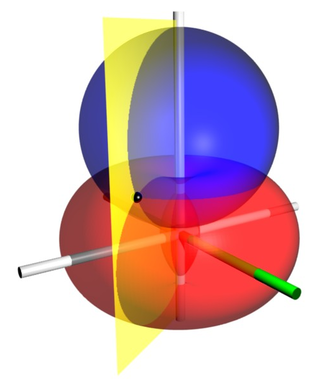
Bispherical coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional bipolar coordinate system about the axis that connects the two foci. Thus, the two foci and in bipolar coordinates remain points in the bispherical coordinate system.

In mathematics, the Struve functionsHα(x), are solutions y(x) of the non-homogeneous Bessel's differential equation:
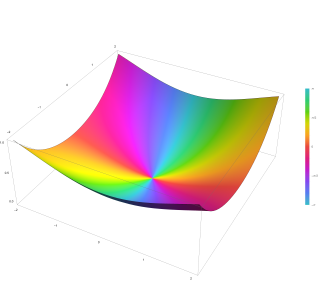
In mathematics, the Anger function, introduced by C. T. Anger, is a function defined as

In fluid dynamics, the mild-slope equation describes the combined effects of diffraction and refraction for water waves propagating over bathymetry and due to lateral boundaries—like breakwaters and coastlines. It is an approximate model, deriving its name from being originally developed for wave propagation over mild slopes of the sea floor. The mild-slope equation is often used in coastal engineering to compute the wave-field changes near harbours and coasts.

Bending of plates, or plate bending, refers to the deflection of a plate perpendicular to the plane of the plate under the action of external forces and moments. The amount of deflection can be determined by solving the differential equations of an appropriate plate theory. The stresses in the plate can be calculated from these deflections. Once the stresses are known, failure theories can be used to determine whether a plate will fail under a given load.
In mathematics, a relative scalar is a scalar-valued function whose transform under a coordinate transform,

In calculus, the integral of the secant function can be evaluated using a variety of methods and there are multiple ways of expressing the antiderivative, all of which can be shown to be equivalent via trigonometric identities,
In mathematics, the Mittag-Leffler polynomials are the polynomials gn(x) or Mn(x) studied by Mittag-Leffler (1891).
Bioche's rules, formulated by the French mathematician Charles Bioche (1859–1949), are rules to aid in the computation of certain indefinite integrals in which the integrand contains sines and cosines.
Some mathematicians defined this type incomplete-version of Bessel function or this type generalized-version of incomplete gamma function:



























































