
In mathematics, a hypergraph is a generalization of a graph in which an edge can join any number of vertices. In contrast, in an ordinary graph, an edge connects exactly two vertices.
In combinatorics, a branch of mathematics, a matroid is a structure that abstracts and generalizes the notion of linear independence in vector spaces. There are many equivalent ways to define a matroid axiomatically, the most significant being in terms of: independent sets; bases or circuits; rank functions; closure operators; and closed sets or flats. In the language of partially ordered sets, a finite simple matroid is equivalent to a geometric lattice.

In mathematics, the Erdős–Ko–Rado theorem limits the number of sets in a family of sets for which every two sets have at least one element in common. Paul Erdős, Chao Ko, and Richard Rado proved the theorem in 1938, but did not publish it until 1961. It is part of the field of combinatorics, and one of the central results of extremal set theory.
In mathematics, and more particularly in set theory, a cover of a set is a family of subsets of whose union is all of . More formally, if is an indexed family of subsets , then is a cover of if . Thus the collection is a cover of if each element of belongs to at least one of the subsets .
In mathematics, a closure operator on a set S is a function :{\mathcal {P}}(S)\rightarrow {\mathcal {P}}(S)} from the power set of S to itself that satisfies the following conditions for all sets
In topology, the nerve complex of a set family is an abstract complex that records the pattern of intersections between the sets in the family. It was introduced by Pavel Alexandrov and now has many variants and generalisations, among them the Čech nerve of a cover, which in turn is generalised by hypercoverings. It captures many of the interesting topological properties in an algorithmic or combinatorial way.
In combinatorics, a greedoid is a type of set system. It arises from the notion of the matroid, which was originally introduced by Whitney in 1935 to study planar graphs and was later used by Edmonds to characterize a class of optimization problems that can be solved by greedy algorithms. Around 1980, Korte and Lovász introduced the greedoid to further generalize this characterization of greedy algorithms; hence the name greedoid. Besides mathematical optimization, greedoids have also been connected to graph theory, language theory, order theory, and other areas of mathematics.

In mathematics, an antimatroid is a formal system that describes processes in which a set is built up by including elements one at a time, and in which an element, once available for inclusion, remains available until it is included. Antimatroids are commonly axiomatized in two equivalent ways, either as a set system modeling the possible states of such a process, or as a formal language modeling the different sequences in which elements may be included. Dilworth (1940) was the first to study antimatroids, using yet another axiomatization based on lattice theory, and they have been frequently rediscovered in other contexts.
In set theory and related branches of mathematics, a family can mean, depending upon the context, any of the following: set, indexed set, multiset, or class. A collection of subsets of a given set is called a family of subsets of , or a family of sets over More generally, a collection of any sets whatsoever is called a family of sets, set family, or a set system. Additionally, a family of sets may be defined as a function from a set , known as the index set, to , in which case the sets of the family are indexed by members of . In some contexts, a family of sets may be allowed to contain repeated copies of any given member, and in other contexts it may form a proper class.

In combinatorics, an abstract simplicial complex (ASC), often called an abstract complex or just a complex, is a family of sets that is closed under taking subsets, i.e., every subset of a set in the family is also in the family. It is a purely combinatorial description of the geometric notion of a simplicial complex. For example, in a 2-dimensional simplicial complex, the sets in the family are the triangles, their edges, and their vertices.
In mathematics, particularly in combinatorics, given a family of sets, here called a collection C, a transversal (also called a cross-section) is a set containing exactly one element from each member of the collection. When the sets of the collection are mutually disjoint, each element of the transversal corresponds to exactly one member of C (the set it is a member of). If the original sets are not disjoint, there are two possibilities for the definition of a transversal:
In mathematics, a field of sets is a mathematical structure consisting of a pair consisting of a set and a family of subsets of called an algebra over that contains the empty set as an element, and is closed under the operations of taking complements in finite unions, and finite intersections.
Pregeometry, and in full combinatorial pregeometry, are essentially synonyms for "matroid". They were introduced by Gian-Carlo Rota with the intention of providing a less "ineffably cacophonous" alternative term. Also, the term combinatorial geometry, sometimes abbreviated to geometry, was intended to replace "simple matroid". These terms are now infrequently used in the study of matroids.

In mathematics, triangulation describes the replacement of topological spaces by piecewise linear spaces, i.e. the choice of a homeomorphism in a suitable simplicial complex. Spaces being homeomorphic to a simplicial complex are called triangulable. Triangulation has various uses in different branches of mathematics, for instance in algebraic topology, in complex analysis or in modeling.

Clique complexes, independence complexes, flag complexes, Whitney complexes and conformal hypergraphs are closely related mathematical objects in graph theory and geometric topology that each describe the cliques of an undirected graph.
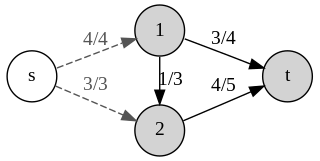
An oriented matroid is a mathematical structure that abstracts the properties of directed graphs, vector arrangements over ordered fields, and hyperplane arrangements over ordered fields. In comparison, an ordinary matroid abstracts the dependence properties that are common both to graphs, which are not necessarily directed, and to arrangements of vectors over fields, which are not necessarily ordered.
In the mathematical theory of matroids, a matroid representation is a family of vectors whose linear independence relation is the same as that of a given matroid. Matroid representations are analogous to group representations; both types of representation provide abstract algebraic structures with concrete descriptions in terms of linear algebra.
In mathematics, a matroid polytope, also called a matroid basis polytope to distinguish it from other polytopes derived from a matroid, is a polytope constructed via the bases of a matroid. Given a matroid , the matroid polytope is the convex hull of the indicator vectors of the bases of .
The independence complex of a graph is a mathematical object describing the independent sets of the graph. Formally, the independence complex of an undirected graph G, denoted by I(G), is an abstract simplicial complex (that is, a family of finite sets closed under the operation of taking subsets), formed by the sets of vertices in the independent sets of G. Any subset of an independent set is itself an independent set, so I(G) is indeed closed under taking subsets.
In mathematics, a basis of a matroid is a maximal independent set of the matroid—that is, an independent set that is not contained in any other independent set.














