
The number e is a mathematical constant approximately equal to 2.71828 that can be characterized in many ways. It is the base of the natural logarithm function. It is the limit of as n tends to infinity, an expression that arises in the computation of compound interest. It is the value at 1 of the (natural) exponential function, commonly denoted It is also the sum of the infinite series

In mathematics, the gamma function is one commonly used extension of the factorial function to complex numbers. The gamma function is defined for all complex numbers except the non-positive integers. For every positive integer n,
In mathematics, a series is, roughly speaking, the operation of adding infinitely many quantities, one after the other, to a given starting quantity. The study of series is a major part of calculus and its generalization, mathematical analysis. Series are used in most areas of mathematics, even for studying finite structures through generating functions. In addition to their ubiquity in mathematics, infinite series are also widely used in other quantitative disciplines such as physics, computer science, statistics and finance.

The natural logarithm of a number is its logarithm to the base of the mathematical constant e, which is an irrational and transcendental number approximately equal to 2.718281828459. The natural logarithm of x is generally written as ln x, logex, or sometimes, if the base e is implicit, simply log x. Parentheses are sometimes added for clarity, giving ln(x), loge(x), or log(x). This is done particularly when the argument to the logarithm is not a single symbol, so as to prevent ambiguity.

In mathematics, the trigonometric functions are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis.
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on. In a finite continued fraction, the iteration/recursion is terminated after finitely many steps by using an integer in lieu of another continued fraction. In contrast, an infinite continued fraction is an infinite expression. In either case, all integers in the sequence, other than the first, must be positive. The integers are called the coefficients or terms of the continued fraction.
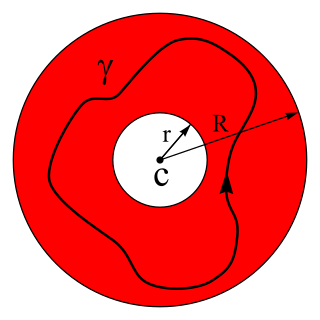
In mathematics, the Laurent series of a complex function is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where a Taylor series expansion cannot be applied. The Laurent series was named after and first published by Pierre Alphonse Laurent in 1843. Karl Weierstrass may have discovered it first in a paper written in 1841, but it was not published until after his death.
In mathematics, a generating function is a representation of an infinite sequence of numbers as the coefficients of a formal power series. Unlike an ordinary series, the formal power series is not required to converge: in fact, the generating function is not actually regarded as a function, and the "variable" remains an indeterminate. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general linear recurrence problem. One can generalize to formal power series in more than one indeterminate, to encode information about infinite multi-dimensional arrays of numbers.
In complex analysis, a branch of mathematics, a generalized continued fraction is a generalization of regular continued fractions in canonical form, in which the partial numerators and partial denominators can assume arbitrary complex values.
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a finite limit.

In mathematics, the lemniscate constantϖ is a transcendental mathematical constant that is the ratio of the perimeter of Bernoulli's lemniscate to its diameter, analogous to the definition of π for the circle. Equivalently, the perimeter of the lemniscate is 2ϖ. The lemniscate constant is closely related to the lemniscate elliptic functions and approximately equal to 2.62205755. The symbol ϖ is a cursive variant of π; see Pi § Variant pi.
In mathematics and theoretical physics, zeta function regularization is a type of regularization or summability method that assigns finite values to divergent sums or products, and in particular can be used to define determinants and traces of some self-adjoint operators. The technique is now commonly applied to problems in physics, but has its origins in attempts to give precise meanings to ill-conditioned sums appearing in number theory.

Approximations for the mathematical constant pi in the history of mathematics reached an accuracy within 0.04% of the true value before the beginning of the Common Era. In Chinese mathematics, this was improved to approximations correct to what corresponds to about seven decimal digits by the 5th century.
In the analytic theory of continued fractions, the convergence problem is the determination of conditions on the partial numeratorsai and partial denominatorsbi that are sufficient to guarantee the convergence of the continued fraction
In the analytic theory of continued fractions, Euler's continued fraction formula is an identity connecting a certain very general infinite series with an infinite continued fraction. First published in 1748, it was at first regarded as a simple identity connecting a finite sum with a finite continued fraction in such a way that the extension to the infinite case was immediately apparent. Today it is more fully appreciated as a useful tool in analytic attacks on the general convergence problem for infinite continued fractions with complex elements.
Ramanujan summation is a technique invented by the mathematician Srinivasa Ramanujan for assigning a value to divergent infinite series. Although the Ramanujan summation of a divergent series is not a sum in the traditional sense, it has properties that make it mathematically useful in the study of divergent infinite series, for which conventional summation is undefined.
In mathematics, for a sequence of complex numbers a1, a2, a3, ... the infinite product
In mathematics, infinite compositions of analytic functions (ICAF) offer alternative formulations of analytic continued fractions, series, products and other infinite expansions, and the theory evolving from such compositions may shed light on the convergence/divergence of these expansions. Some functions can actually be expanded directly as infinite compositions. In addition, it is possible to use ICAF to evaluate solutions of fixed point equations involving infinite expansions. Complex dynamics offers another venue for iteration of systems of functions rather than a single function. For infinite compositions of a single function see Iterated function. For compositions of a finite number of functions, useful in fractal theory, see Iterated function system.











