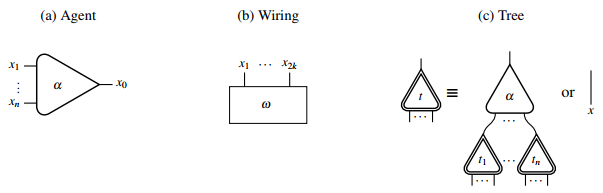
Interaction calculus
Textual representation of interaction nets is called the interaction calculus [4] and can be seen as a programming language.
Inductively defined trees correspond to terms in the interaction calculus, where
in the interaction calculus, where  is called a name.
is called a name.
Any interaction net  can be redrawn using the previously defined wiring and tree primitives as follows:
can be redrawn using the previously defined wiring and tree primitives as follows:

which in the interaction calculus corresponds to a configuration
 ,
,
where  ,
,  , and
, and  are arbitrary terms. The ordered sequence
are arbitrary terms. The ordered sequence  in the left-hand side is called an interface, while the right-hand side contains an unordered multiset of equations
in the left-hand side is called an interface, while the right-hand side contains an unordered multiset of equations . Wiring
. Wiring  translates to names, and each name has to occur exactly twice in a configuration.
translates to names, and each name has to occur exactly twice in a configuration.
Just like in the  -calculus, the interaction calculus has the notions of
-calculus, the interaction calculus has the notions of  -conversion and substitution naturally defined on configurations. Specifically, both occurrences of any name can be replaced with a new name if the latter does not occur in a given configuration. Configurations are considered equivalent up to
-conversion and substitution naturally defined on configurations. Specifically, both occurrences of any name can be replaced with a new name if the latter does not occur in a given configuration. Configurations are considered equivalent up to  -conversion. In turn, substitution
-conversion. In turn, substitution  is the result of replacing the name
is the result of replacing the name  in a term
in a term  with another term
with another term  if
if  has exactly one occurrence in the term
has exactly one occurrence in the term  .
.
Any interaction rule can be graphically represented as follows:
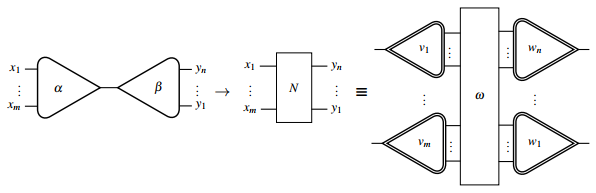
where  , and the interaction net
, and the interaction net  on the right-hand side is redrawn using the wiring and tree primitives in order to translate into the interaction calculus as
on the right-hand side is redrawn using the wiring and tree primitives in order to translate into the interaction calculus as  using Lafont's notation.
using Lafont's notation.
The interaction calculus defines reduction on configurations in more details than seen from graph rewriting defined on interaction nets. Namely, if  , the following reduction:
, the following reduction:

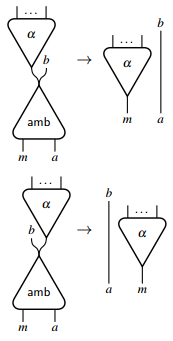
is called interaction. When one of equations has the form of  , indirection can be applied resulting in substitution of the other occurrence of the name
, indirection can be applied resulting in substitution of the other occurrence of the name  in some term
in some term  :
:
 or
or  .
.
An equation  is called a deadlock if
is called a deadlock if  has occurrence in term
has occurrence in term  . Generally only deadlock-free interaction nets are considered. Together, interaction and indirection define the reduction relation on configurations. The fact that configuration
. Generally only deadlock-free interaction nets are considered. Together, interaction and indirection define the reduction relation on configurations. The fact that configuration  reduces to its normal form
reduces to its normal form with no equations left is denoted as
with no equations left is denoted as  .
.
Interaction combinators
One of the simplest interaction systems that can simulate any other interaction system is that of interaction combinators. [5] Its signature is  with
with  and
and  . Interaction rules for these agents are:
. Interaction rules for these agents are:
 called erasing;
called erasing; called duplication;
called duplication; and
and  called annihilation.
called annihilation.
Graphically, the erasing and duplication rules can be represented as follows:
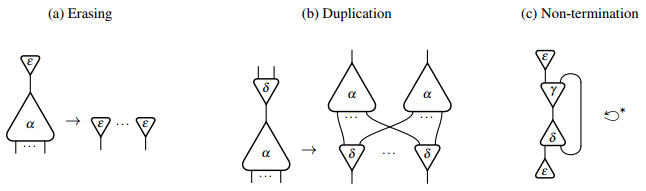
with an example of a non-terminating interaction net that reduces to itself. Its infinite reduction sequence starting from the corresponding configuration in the interaction calculus is as follows: