
The knapsack problem is the following problem in combinatorial optimization:

Linear programming (LP), also called linear optimization, is a method to achieve the best outcome in a mathematical model whose requirements and objective are represented by linear relationships. Linear programming is a special case of mathematical programming.
Constraint programming (CP) is a paradigm for solving combinatorial problems that draws on a wide range of techniques from artificial intelligence, computer science, and operations research. In constraint programming, users declaratively state the constraints on the feasible solutions for a set of decision variables. Constraints differ from the common primitives of imperative programming languages in that they do not specify a step or sequence of steps to execute, but rather the properties of a solution to be found. In addition to constraints, users also need to specify a method to solve these constraints. This typically draws upon standard methods like chronological backtracking and constraint propagation, but may use customized code like a problem-specific branching heuristic.
Constraint satisfaction problems (CSPs) are mathematical questions defined as a set of objects whose state must satisfy a number of constraints or limitations. CSPs represent the entities in a problem as a homogeneous collection of finite constraints over variables, which is solved by constraint satisfaction methods. CSPs are the subject of research in both artificial intelligence and operations research, since the regularity in their formulation provides a common basis to analyze and solve problems of many seemingly unrelated families. CSPs often exhibit high complexity, requiring a combination of heuristics and combinatorial search methods to be solved in a reasonable time. Constraint programming (CP) is the field of research that specifically focuses on tackling these kinds of problems. Additionally, the Boolean satisfiability problem (SAT), satisfiability modulo theories (SMT), mixed integer programming (MIP) and answer set programming (ASP) are all fields of research focusing on the resolution of particular forms of the constraint satisfaction problem.
An integer programming problem is a mathematical optimization or feasibility program in which some or all of the variables are restricted to be integers. In many settings the term refers to integer linear programming (ILP), in which the objective function and the constraints are linear.
In the mathematical field of graph theory, a graph homomorphism is a mapping between two graphs that respects their structure. More concretely, it is a function between the vertex sets of two graphs that maps adjacent vertices to adjacent vertices.
In constraint satisfaction, the AC-3 algorithm is one of a series of algorithms used for the solution of constraint satisfaction problems. It was developed by Alan Mackworth in 1977. The earlier AC algorithms are often considered too inefficient, and many of the later ones are difficult to implement, and so AC-3 is the one most often taught and used in very simple constraint solvers.
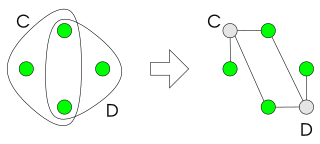
The hidden transformation reformulates a constraint satisfaction problem in such a way all constraints have at most two variables. The new problem is satisfiable if and only if the original problem was, and solutions can be converted easily from one problem to the other.
In computer science, the min-conflicts algorithm is a search algorithm or heuristic method to solve constraint satisfaction problems.
In constraint satisfaction, local consistency conditions are properties of constraint satisfaction problems related to the consistency of subsets of variables or constraints. They can be used to reduce the search space and make the problem easier to solve. Various kinds of local consistency conditions are leveraged, including node consistency, arc consistency, and path consistency.
The dual problem is a reformulation of a constraint satisfaction problem expressing each constraint of the original problem as a variable. Dual problems only contain binary constraints, and are therefore solvable by algorithms tailored for such problems. The join graphs and join trees of a constraint satisfaction problem are graphs representing its dual problem or a problem obtained from the dual problem removing some redundant constraints.

In constraint satisfaction, local search is an incomplete method for finding a solution to a problem. It is based on iteratively improving an assignment of the variables until all constraints are satisfied. In particular, local search algorithms typically modify the value of a variable in an assignment at each step. The new assignment is close to the previous one in the space of assignment, hence the name local search.
In mathematical optimization, constrained optimization is the process of optimizing an objective function with respect to some variables in the presence of constraints on those variables. The objective function is either a cost function or energy function, which is to be minimized, or a reward function or utility function, which is to be maximized. Constraints can be either hard constraints, which set conditions for the variables that are required to be satisfied, or soft constraints, which have some variable values that are penalized in the objective function if, and based on the extent that, the conditions on the variables are not satisfied.
Constraint logic programming is a form of constraint programming, in which logic programming is extended to include concepts from constraint satisfaction. A constraint logic program is a logic program that contains constraints in the body of clauses. An example of a clause including a constraint is A(X,Y):-X+Y>0,B(X),C(Y). In this clause, X+Y>0 is a constraint; A(X,Y), B(X), and C(Y) are literals as in regular logic programming. This clause states one condition under which the statement A(X,Y) holds: X+Y is greater than zero and both B(X) and C(Y) are true.
Distributed constraint optimization is the distributed analogue to constraint optimization. A DCOP is a problem in which a group of agents must distributedly choose values for a set of variables such that the cost of a set of constraints over the variables is minimized.
The complexity of constraint satisfaction is the application of computational complexity theory to constraint satisfaction. It has mainly been studied for discriminating between tractable and intractable classes of constraint satisfaction problems on finite domains.
In computational complexity theory, a branch of computer science, Schaefer's dichotomy theorem, proved by Thomas Jerome Schaefer, states necessary and sufficient conditions under which a finite set S of relations over the Boolean domain yields polynomial-time or NP-complete problems when the relations of S are used to constrain some of the propositional variables. It is called a dichotomy theorem because the complexity of the problem defined by S is either in P or is NP-complete, as opposed to one of the classes of intermediate complexity that is known to exist by Ladner's theorem.
In constraint satisfaction, a decomposition method translates a constraint satisfaction problem into another constraint satisfaction problem that is binary and acyclic. Decomposition methods work by grouping variables into sets, and solving a subproblem for each set. These translations are done because solving binary acyclic problems is a tractable problem.
Semidefinite programming (SDP) is a subfield of mathematical programming concerned with the optimization of a linear objective function over the intersection of the cone of positive semidefinite matrices with an affine space, i.e., a spectrahedron.
In artificial intelligence and operations research, a Weighted Constraint Satisfaction Problem (WCSP) is a generalization of a constraint satisfaction problem (CSP) where some of the constraints can be violated and in which preferences among solutions can be expressed. This generalization makes it possible to represent more real-world problems, in particular those that are over-constrained, or those where we want to find a minimal-cost solution among multiple possible solutions.










