In geometry, the isotomic conjugate of a point P with respect to a triangle ABC is another point, defined in a specific way from P and ABC: If the base points of the lines PA, PB, and PC on the sides opposite A, B, and C are reflected about the midpoints of their respective sides, the resulting lines intersect at the isotomic conjugate of P.
We assume that P is not collinear with any two vertices of ABC. Let A', B' and C' be the points in which the lines AP, BP, CP meet sidelines BC, CA and AB (extended if necessary). Reflecting A', B', C' in the midpoints of sides BC, CA, AB will give points A", B" and C" respectively. The isotomic linesAA", BB" and CC" joining these new points to the vertices meet at a point (which can be proved using Ceva's theorem), the isotomic conjugate of P.
If the trilinears for P are p : q : r, then the trilinears for the isotomic conjugate of P are
where a, b and c are the side lengths opposite vertices A, B, and C respectively.
The isotomic conjugate of the centroid of triangle ABC is the centroid itself.
The isotomic conjugate of the symmedian point is the third Brocard point, and the isotomic conjugate of the Gergonne point is the Nagel point.
Isotomic conjugates of lines are circumconics, and conversely, isotomic conjugates of circumconics are lines. (This property holds for isogonal conjugates as well.)
In geometry, a pedal triangle is obtained by projecting a point onto the sides of a triangle.
In geometry, an altitude of a triangle is a line segment through a vertex and perpendicular to a line containing the base. This line containing the opposite side is called the extended base of the altitude. The intersection of the extended base and the altitude is called the foot of the altitude. The length of the altitude, often simply called "the altitude", is the distance between the extended base and the vertex. The process of drawing the altitude from the vertex to the foot is known as dropping the altitude at that vertex. It is a special case of orthogonal projection.
In mathematics and physics, the centroid or geometric center of a plane figure is the arithmetic mean position of all the points in the figure. Informally, it is the point at which a cutout of the shape could be perfectly balanced on the tip of a pin.
In geometry, the incenter of a triangle is a triangle center, a point defined for any triangle in a way that is independent of the triangle's placement or scale. The incenter may be equivalently defined as the point where the internal angle bisectors of the triangle cross, as the point equidistant from the triangle's sides, as the junction point of the medial axis and innermost point of the grassfire transform of the triangle, and as the center point of the inscribed circle of the triangle.
In geometry, symmedians are three particular geometrical lines associated with every triangle. They are constructed by taking a median of the triangle, and reflecting the line over the corresponding angle bisector. The angle formed by the symmedian and the angle bisector has the same measure as the angle between the median and the angle bisector, but it is on the other side of the angle bisector.
In geometry, the midpoint is the middle point of a line segment. It is equidistant from both endpoints, and it is the centroid both of the segment and of the endpoints. It bisects the segment.
In the geometry of triangles, the incircle and nine-point circle of a triangle are internally tangent to each other at the Feuerbach point of the triangle. The Feuerbach point is a triangle center, meaning that its definition does not depend on the placement and scale of the triangle. It is listed as X(11) in Clark Kimberling's Encyclopedia of Triangle Centers, and is named after Karl Wilhelm Feuerbach.
In mathematics, a cubic plane curve is a plane algebraic curve C defined by a cubic equation
In geometry, the isogonal conjugate of a point P with respect to a triangle ABC is constructed by reflecting the lines PA, PB, and PC about the angle bisectors of A, B, and C respectively. These three reflected lines concur at the isogonal conjugate of P. This is a direct result of the trigonometric form of Ceva's theorem.
The medial triangle or midpoint triangle of a triangle ABC is the triangle with vertices at the midpoints of the triangle's sides AB, AC and BC. It is the n=3 case of the midpoint polygon of a polygon with n sides. The medial triangle is not the same thing as the median triangle, which is the triangle whose sides have the same lengths as the medians of ABC.
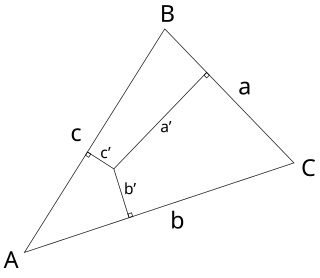
In geometry, the trilinear coordinatesx:y:z of a point relative to a given triangle describe the relative directed distances from the three sidelines of the triangle. Trilinear coordinates are an example of homogeneous coordinates. The ratio x:y is the ratio of the perpendicular distances from the point to the sides opposite vertices A and B respectively; the ratio y:z is the ratio of the perpendicular distances from the point to the sidelines opposite vertices B and C respectively; and likewise for z:x and vertices C and A.
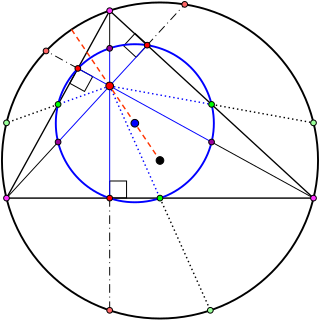
In geometry, the nine-point center is a triangle center, a point defined from a given triangle in a way that does not depend on the placement or scale of the triangle. It is so called because it is the center of the nine-point circle, a circle that passes through nine significant points of the triangle: the midpoints of the three edges, the feet of the three altitudes, and the points halfway between the orthocenter and each of the three vertices. The nine-point center is listed as point X(5) in Clark Kimberling's Encyclopedia of Triangle Centers.
In Euclidean geometry, the isodynamic points of a triangle are points associated with the triangle, with the properties that an inversion centered at one of these points transforms the given triangle into an equilateral triangle, and that the distances from the isodynamic point to the triangle vertices are inversely proportional to the opposite side lengths of the triangle. Triangles that are similar to each other have isodynamic points in corresponding locations in the plane, so the isodynamic points are triangle centers, and unlike other triangle centers the isodynamic points are also invariant under Möbius transformations. A triangle that is itself equilateral has a unique isodynamic point, at its centroid; every non-equilateral triangle has two isodynamic points. Isodynamic points were first studied and named by Joseph Neuberg (1885).
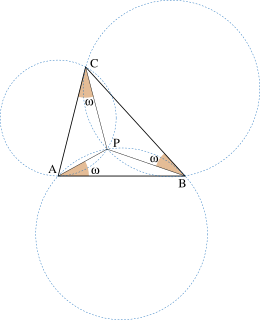
In geometry, Brocard points are special points within a triangle. They are named after Henri Brocard (1845–1922), a French mathematician.
In geometry, the Nagel point is a triangle center, one of the points associated with a given triangle whose definition does not depend on the placement or scale of the triangle. The Nagel point is named after Christian Heinrich von Nagel.
In triangle geometry, a circumconic is a conic section that passes through the three vertices of a triangle, and an inconic is a conic section inscribed in the sides, possibly extended, of a triangle.
In geometry, a triangle center is a point in the plane that is in some sense a center of a triangle akin to the centers of squares and circles, that is, a point that is in the middle of the figure by some measure. For example the centroid, circumcenter, incenter and orthocenter were familiar to the ancient Greeks, and can be obtained by simple constructions.
In geometry, the Steiner inellipse, midpoint inellipse, or midpoint ellipse of a triangle is the unique ellipse inscribed in the triangle and tangent to the sides at their midpoints. It is an example of an inellipse. By comparison the inscribed circle and Mandart inellipse of a triangle are other inconics that are tangent to the sides, but not at the midpoints unless the triangle is equilateral. The Steiner inellipse is attributed by Dörrie to Jakob Steiner, and a proof of its uniqueness is given by Dan Kalman.
In geometry, central lines are certain special straight lines that lie in the plane of a triangle. The special property that distinguishes a straight line as a central line is manifested via the equation of the line in trilinear coordinates. This special property is related to the concept of triangle center also. The concept of a central line was introduced by Clark Kimberling in a paper published in 1994.
In geometry, trilinear polarity is a certain correspondence between the points in the plane of a triangle not lying on the sides of the triangle and lines in the plane of the triangle not passing through the vertices of the triangle. "Although it is called a polarity, it is not really a polarity at all, for poles of concurrent lines are not collinear points." It was Poncelet (1788–1867), a French engineer and mathematician, who introduced the idea of the trilinear polar of a point in 1865.