In geometry, the Nagel point (named for Christian Heinrich von Nagel) is a triangle center, one of the points associated with a given triangle whose definition does not depend on the placement or scale of the triangle. It is the point of concurrency of all three of the triangle's splitters.
Given a triangle △ABC, let TA, TB, TC be the extouch points in which the A-excircle meets line BC, the B-excircle meets line CA, and the C-excircle meets line AB, respectively. The lines ATA, BTB, CTC concur in the Nagel point N of triangle △ABC.
Another construction of the point TA is to start at A and trace around triangle △ABC half its perimeter, and similarly for TB and TC. Because of this construction, the Nagel point is sometimes also called the bisected perimeter point, and the segments ATA, BTB, CTC are called the triangle's splitters.
There exists an easy construction of the Nagel point. Starting from each vertex of a triangle, it suffices to carry twice the length of the opposite edge. We obtain three lines which concur at the Nagel point. [1]
The Nagel point is the isotomic conjugate of the Gergonne point. The Nagel point, the centroid, and the incenter are collinear on a line called the Nagel line. The incenter is the Nagel point of the medial triangle; [2] [3] equivalently, the Nagel point is the incenter of the anticomplementary triangle. The isogonal conjugate of the Nagel point is the point of concurrency of the lines joining the mixtilinear touchpoint and the opposite vertex.
The un-normalized barycentric coordinates of the Nagel point are where is the semi-perimeter of the reference triangle △ABC.
The trilinear coordinates of the Nagel point are [4] as
or, equivalently, in terms of the side lengths
The Nagel point is named after Christian Heinrich von Nagel, a nineteenth-century German mathematician, who wrote about it in 1836. Early contributions to the study of this point were also made by August Leopold Crelle and Carl Gustav Jacob Jacobi. [5]
In geometry, bisection is the division of something into two equal or congruent parts. Usually it involves a bisecting line, also called a bisector. The most often considered types of bisectors are the segment bisector, a line that passes through the midpoint of a given segment, and the angle bisector, a line that passes through the apex of an angle . In three-dimensional space, bisection is usually done by a bisecting plane, also called the bisector.
The orthocenter of a triangle, usually denoted by H, is the point where the three altitudes intersect. The orthocenter lies inside the triangle if and only if the triangle is acute. For a right triangle, the orthocenter coincides with the vertex at the right angle.
In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches the three sides. The center of the incircle is a triangle center called the triangle's incenter.
In geometry, an orthocentric system is a set of four points on a plane, one of which is the orthocenter of the triangle formed by the other three. Equivalently, the lines passing through disjoint pairs among the points are perpendicular, and the four circles passing through any three of the four points have the same radius.
In mathematics and physics, the centroid, also known as geometric center or center of figure, of a plane figure or solid figure is the arithmetic mean position of all the points in the surface of the figure. The same definition extends to any object in -dimensional Euclidean space.
In geometry, the incenter of a triangle is a triangle center, a point defined for any triangle in a way that is independent of the triangle's placement or scale. The incenter may be equivalently defined as the point where the internal angle bisectors of the triangle cross, as the point equidistant from the triangle's sides, as the junction point of the medial axis and innermost point of the grassfire transform of the triangle, and as the center point of the inscribed circle of the triangle.
In geometry, the semiperimeter of a polygon is half its perimeter. Although it has such a simple derivation from the perimeter, the semiperimeter appears frequently enough in formulas for triangles and other figures that it is given a separate name. When the semiperimeter occurs as part of a formula, it is typically denoted by the letter s.
In geometry, the circumscribed circle or circumcircle of a triangle is a circle that passes through all three vertices. The center of this circle is called the circumcenter of the triangle, and its radius is called the circumradius. The circumcenter is the point of intersection between the three perpendicular bisectors of the triangle's sides, and is a triangle center.
In geometry, collinearity of a set of points is the property of their lying on a single line. A set of points with this property is said to be collinear. In greater generality, the term has been used for aligned objects, that is, things being "in a line" or "in a row".
In geometry, a cevian is a line segment which joins a vertex of a triangle to a point on the opposite side of the triangle. Medians and angle bisectors are special cases of cevians. The name "cevian" comes from the Italian mathematician Giovanni Ceva, who proved a well-known theorem about cevians which also bears his name.
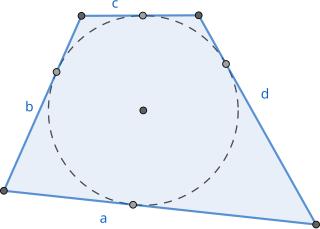
In Euclidean geometry, a tangential quadrilateral or circumscribed quadrilateral is a convex quadrilateral whose sides all can be tangent to a single circle within the quadrilateral. This circle is called the incircle of the quadrilateral or its inscribed circle, its center is the incenter and its radius is called the inradius. Since these quadrilaterals can be drawn surrounding or circumscribing their incircles, they have also been called circumscribable quadrilaterals, circumscribing quadrilaterals, and circumscriptible quadrilaterals. Tangential quadrilaterals are a special case of tangential polygons.
In geometry, the incircle of the medial triangle of a triangle is the Spieker circle, named after 19th-century German geometer Theodor Spieker. Its center, the Spieker center, in addition to being the incenter of the medial triangle, is the center of mass of the uniform-density boundary of triangle. The Spieker center is also the point where all three cleavers of the triangle intersect each other.
In Euclidean geometry, the extouch triangle of a triangle is formed by joining the points at which the three excircles touch the triangle.
In geometry, the mittenpunkt of a triangle is a triangle center: a point defined from the triangle that is invariant under Euclidean transformations of the triangle. It was identified in 1836 by Christian Heinrich von Nagel as the symmedian point of the excentral triangle of the given triangle.
In geometry, the Spieker center is a special point associated with a plane triangle. It is defined as the center of mass of the perimeter of the triangle. The Spieker center of a triangle △ABC is the center of gravity of a homogeneous wire frame in the shape of △ABC. The point is named in honor of the 19th-century German geometer Theodor Spieker. The Spieker center is a triangle center and it is listed as the point X(10) in Clark Kimberling's Encyclopedia of Triangle Centers.
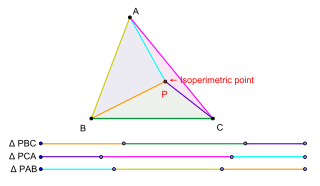
In geometry, the isoperimetric point is a triangle center — a special point associated with a plane triangle. The term was originally introduced by G.R. Veldkamp in a paper published in the American Mathematical Monthly in 1985 to denote a point P in the plane of a triangle △ABC having the property that the triangles △PBC, △PCA, △PAB have isoperimeters, that is, having the property that
In geometry, central lines are certain special straight lines that lie in the plane of a triangle. The special property that distinguishes a straight line as a central line is manifested via the equation of the line in trilinear coordinates. This special property is related to the concept of triangle center also. The concept of a central line was introduced by Clark Kimberling in a paper published in 1994.
In geometry, the Bevan point, named after Benjamin Bevan, is a triangle center. It is defined as center of the Bevan circle, that is the circle through the centers of the three excircles of a triangle.
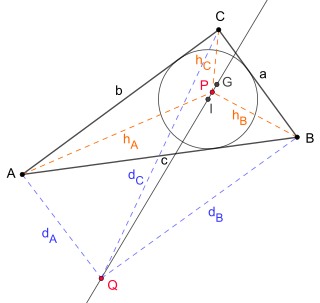
In Euclidean geometry, the equal detour point is a triangle center denoted by X(176) in Clark Kimberling's Encyclopedia of Triangle Centers. It is characterized by the equal detour property: if one travels from any vertex of a triangle △ABC to another by taking a detour through some inner point P, then the additional distance traveled is constant. This means the following equation has to hold:
In geometry, the Feuerbach hyperbola is a rectangular hyperbola passing through important triangle centers such as the Orthocenter, Gergonne point, Nagel point and Schiffler point. The center of the hyperbola is the Feuerbach point, the point of tangency of the incircle and the nine-point circle.
