In geometry, the Mandart inellipse of a triangle is an ellipse inscribed within the triangle, tangent to its sides at the contact points of its excircles (which are also the vertices of the extouch triangle and the endpoints of the splitters). [1] The Mandart inellipse is named after H. Mandart, who studied it in two papers published in the late 19th century. [2] [3]
As an inconic, the Mandart inellipse is described by the parameters
where a, b, and c are sides of the given triangle.
The center of the Mandart inellipse is the mittenpunkt of the triangle. The three lines connecting the triangle vertices to the opposite points of tangency all meet in a single point, the Nagel point of the triangle. [2]
In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. As such, it generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity e, a number ranging from e = 0 to e = 1.
In mathematics, a hyperbola is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows. The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane and a double cone. If the plane intersects both halves of the double cone but does not pass through the apex of the cones, then the conic is a hyperbola.
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices A, B, and C is denoted .
In geometry, the nine-point circle is a circle that can be constructed for any given triangle. It is so named because it passes through nine significant concyclic points defined from the triangle. These nine points are:
In geometry, the incircle or inscribed circle of a triangle is the largest circle contained in the triangle; it touches the three sides. The center of the incircle is a triangle center called the triangle's incenter.
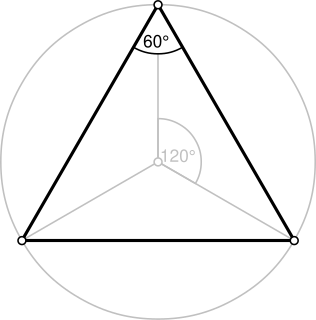
In geometry, an equilateral triangle is a triangle in which all three sides have the same length. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each other and are each 60°. It is also a regular polygon, so it is also referred to as a regular triangle.
In mathematics and physics, the centroid or geometric center of a plane figure is the arithmetic mean position of all the points in the figure. Informally, it is the point at which a cutout of the shape could be perfectly balanced on the tip of a pin.
In geometry, the incenter of a triangle is a triangle center, a point defined for any triangle in a way that is independent of the triangle's placement or scale. The incenter may be equivalently defined as the point where the internal angle bisectors of the triangle cross, as the point equidistant from the triangle's sides, as the junction point of the medial axis and innermost point of the grassfire transform of the triangle, and as the center point of the inscribed circle of the triangle.
In geometry, the midpoint is the middle point of a line segment. It is equidistant from both endpoints, and it is the centroid both of the segment and of the endpoints. It bisects the segment.
In the geometry of triangles, the incircle and nine-point circle of a triangle are internally tangent to each other at the Feuerbach point of the triangle. The Feuerbach point is a triangle center, meaning that its definition does not depend on the placement and scale of the triangle. It is listed as X(11) in Clark Kimberling's Encyclopedia of Triangle Centers, and is named after Karl Wilhelm Feuerbach.
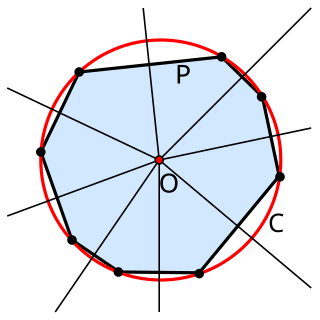
In geometry, the circumscribed circle or circumcircle of a polygon is a circle that passes through all the vertices of the polygon. The center of this circle is called the circumcenter and its radius is called the circumradius.
In geometry, collinearity of a set of points is the property of their lying on a single line. A set of points with this property is said to be collinear. In greater generality, the term has been used for aligned objects, that is, things being "in a line" or "in a row".
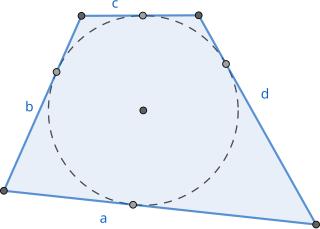
In Euclidean geometry, a tangential quadrilateral or circumscribed quadrilateral is a convex quadrilateral whose sides all can be tangent to a single circle within the quadrilateral. This circle is called the incircle of the quadrilateral or its inscribed circle, its center is the incenter and its radius is called the inradius. Since these quadrilaterals can be drawn surrounding or circumscribing their incircles, they have also been called circumscribable quadrilaterals, circumscribing quadrilaterals, and circumscriptible quadrilaterals. Tangential quadrilaterals are a special case of tangential polygons.
In triangle geometry, a circumconic is a conic section that passes through the three vertices of a triangle, and an inconic is a conic section inscribed in the sides, possibly extended, of a triangle.
In geometry, the extouch triangle of a triangle is formed by joining the points at which the three excircles touch the triangle.
In plane geometry, a splitter is a line segment through one of the vertices of a triangle that bisects the perimeter of the triangle.
In mathematics, Marden's theorem, named after Morris Marden but proved about 100 years earlier by Jörg Siebeck, gives a geometric relationship between the zeroes of a third-degree polynomial with complex coefficients and the zeroes of its derivative. See also geometrical properties of polynomial roots.
In geometry, the Steiner inellipse, midpoint inellipse, or midpoint ellipse of a triangle is the unique ellipse inscribed in the triangle and tangent to the sides at their midpoints. It is an example of an inellipse. By comparison the inscribed circle and Mandart inellipse of a triangle are other inconics that are tangent to the sides, but not at the midpoints unless the triangle is equilateral. The Steiner inellipse is attributed by Dörrie to Jakob Steiner, and a proof of its uniqueness is given by Dan Kalman.
In geometry, the Steiner ellipse of a triangle, also called the Steiner circumellipse to distinguish it from the Steiner inellipse, is the unique circumellipse whose center is the triangle's centroid. Named after Jakob Steiner, it is an example of a circumconic. By comparison the circumcircle of a triangle is another circumconic that touches the triangle at its vertices, but is not centered at the triangle's centroid unless the triangle is equilateral.
In triangle geometry, an inellipse is an ellipse that touches the three sides of a triangle. The simplest example is the incircle. Further important inellipses are the Steiner inellipse, which touches the triangle at the midpoints of its sides, the Mandart inellipse and Brocard inellipse. For any triangle there exist an infinite number of inellipses.
