In geometry, the mittenpunkt (German, middlespoint) of a triangle is a triangle center: a point defined from the triangle that is invariant under Euclidean transformations of the triangle. It was identified in 1836 by Christian Heinrich von Nagel as the symmedian point of the excentral triangle of the given triangle. [1] [2]
The mittenpunkt has trilinear coordinates [1]
where a, b, and c are the side lengths of the given triangle. Expressed instead in terms of the angles A, B, and C, the trilinears are [3]
The barycentric coordinates are [3]
The mittenpunkt is at the intersection of the line connecting the centroid and the Gergonne point, the line connecting the incenter and the symmedian point and the line connecting the orthocenter with the Spieker center, thus establishing three collinearities involving the mittenpunkt. [4]
The three lines connecting the excenters of the given triangle to the corresponding edge midpoints all meet at the mittenpunkt; thus, it is the center of perspective of the excentral triangle and the median triangle, with the corresponding axis of perspective being the trilinear polar of the Gergonne point. [5] The mittenpunkt is also the centroid of the Mandart inellipse of the given triangle, the ellipse tangent to the triangle at its extouch points. [6]
The Mittenpunkt also serves as the Gergonne point of the Medial triangle.
In geometry, an altitude of a triangle is a line segment through a vertex and perpendicular to a line containing the base. This line containing the opposite side is called the extended base of the altitude. The intersection of the extended base and the altitude is called the foot of the altitude. The length of the altitude, often simply called "the altitude", is the distance between the extended base and the vertex. The process of drawing the altitude from the vertex to the foot is known as dropping the altitude at that vertex. It is a special case of orthogonal projection.
In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches the three sides. The center of the incircle is a triangle center called the triangle's incenter.
In mathematics and physics, the centroid, also known as geometric center or center of figure, of a plane figure or solid figure is the arithmetic mean position of all the points in the surface of the figure. The same definition extends to any object in n-dimensional Euclidean space.
In geometry, the Euler line, named after Leonhard Euler, is a line determined from any triangle that is not equilateral. It is a central line of the triangle, and it passes through several important points determined from the triangle, including the orthocenter, the circumcenter, the centroid, the Exeter point and the center of the nine-point circle of the triangle.
In geometry, the incenter of a triangle is a triangle center, a point defined for any triangle in a way that is independent of the triangle's placement or scale. The incenter may be equivalently defined as the point where the internal angle bisectors of the triangle cross, as the point equidistant from the triangle's sides, as the junction point of the medial axis and innermost point of the grassfire transform of the triangle, and as the center point of the inscribed circle of the triangle.
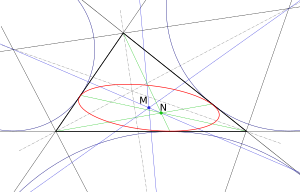
In mathematics, a cubic plane curve is a plane algebraic curve C defined by a cubic equation
In geometry, a barycentric coordinate system is a coordinate system in which the location of a point is specified by reference to a simplex. The barycentric coordinates of a point can be interpreted as masses placed at the vertices of the simplex, such that the point is the center of mass of these masses. These masses can be zero or negative; they are all positive if and only if the point is inside the simplex.
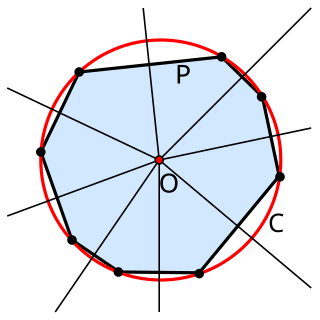
In geometry, the circumscribed circle or circumcircle of a polygon is a circle that passes through all the vertices of the polygon. The center of this circle is called the circumcenter and its radius is called the circumradius.
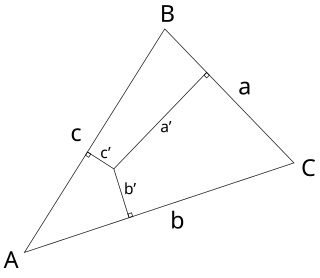
In geometry, the trilinear coordinatesx : y : z of a point relative to a given triangle describe the relative directed distances from the three sidelines of the triangle. Trilinear coordinates are an example of homogeneous coordinates. The ratio x : y is the ratio of the perpendicular distances from the point to the sides opposite vertices A and B respectively; the ratio y : z is the ratio of the perpendicular distances from the point to the sidelines opposite vertices B and C respectively; and likewise for z : x and vertices C and A.
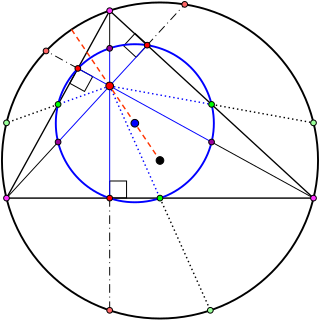
In geometry, the nine-point center is a triangle center, a point defined from a given triangle in a way that does not depend on the placement or scale of the triangle. It is so called because it is the center of the nine-point circle, a circle that passes through nine significant points of the triangle: the midpoints of the three edges, the feet of the three altitudes, and the points halfway between the orthocenter and each of the three vertices. The nine-point center is listed as point X(5) in Clark Kimberling's Encyclopedia of Triangle Centers.
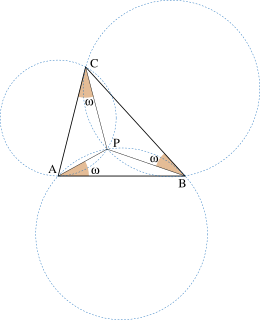
In geometry, Brocard points are special points within a triangle. They are named after Henri Brocard (1845–1922), a French mathematician.
In geometry, the Nagel point is a triangle center, one of the points associated with a given triangle whose definition does not depend on the placement or scale of the triangle. The Nagel point is named after Christian Heinrich von Nagel.
In Euclidean geometry, a circumconic is a conic section that passes through the three vertices of a triangle, and an inconic is a conic section inscribed in the sides, possibly extended, of a triangle.
In geometry, the extouch triangle of a triangle is formed by joining the points at which the three excircles touch the triangle.
In geometry, a triangle center is a point in the plane that is in some sense a center of a triangle akin to the centers of squares and circles, that is, a point that is in the middle of the figure by some measure. For example, the centroid, circumcenter, incenter and orthocenter were familiar to the ancient Greeks, and can be obtained by simple constructions.
In geometry, Napoleon points are a pair of special points associated with a plane triangle. It is generally believed that the existence of these points was discovered by Napoleon Bonaparte, the Emperor of the French from 1804 to 1815, but many have questioned this belief. The Napoleon points are triangle centers and they are listed as the points X(17) and X(18) in Clark Kimberling's Encyclopedia of Triangle Centers.
In triangle geometry, the Steiner point is a particular point associated with a triangle. It is a triangle center and it is designated as the center X(99) in Clark Kimberling's Encyclopedia of Triangle Centers. Jakob Steiner (1796–1863), Swiss mathematician, described this point in 1826. The point was given Steiner's name by Joseph Neuberg in 1886.
In geometry, central lines are certain special straight lines that lie in the plane of a triangle. The special property that distinguishes a straight line as a central line is manifested via the equation of the line in trilinear coordinates. This special property is related to the concept of triangle center also. The concept of a central line was introduced by Clark Kimberling in a paper published in 1994.
In geometry, the Feuerbach hyperbola is a rectangular hyperbola passing through important triangle centers such as the Orthocenter, Gergonne point, Nagel point and Shiffler point. The center of the hyperbola is the Feuerbach point, the point of tangency of the incircle and the nine-point circle.
