Perspective (geometry)

Last updated June 06, 2024

Two figures in a plane are perspective from a point O, called the center of perspectivity, if the lines joining corresponding points of the figures all meet at O. Dually, the figures are said to be perspective from a line if the points of intersection of corresponding lines all lie on one line. The proper setting for this concept is in projective geometry where there will be no special cases due to parallel lines since all lines meet. Although stated here for figures in a plane, the concept is easily extended to higher dimensions.

Terminology

The line which goes through the points where the figure's corresponding sides intersect is known as the axis of perspectivity, perspective axis, homology axis, or archaically, perspectrix. The figures are said to be perspective from this axis. The point at which the lines joining the corresponding vertices of the perspective figures intersect is called the center of perspectivity, perspective center, homology center, pole, or archaically perspector. The figures are said to be perspective from this center.^[1]

Perspectivity

If each of the perspective figures consists of all the points on a line (a range) then transformation of the points of one range to the other is called a central perspectivity. A dual transformation, taking all the lines through a point (a pencil) to another pencil by means of an axis of perspectivity is called an axial perspectivity.^[2]

Triangles

An important special case occurs when the figures are triangles. Two triangles that are perspective from a point are said to be centrally perspective and are called a central couple. Two triangles that are perspective from a line are called axially perspective and an axial couple.^[3]

Notation

Karl von Staudt introduced the notation $ABC\doublebarwedge abc$ to indicate that triangles ABC and abc are perspective.^[4]

Related theorems and configurations

Desargues' theorem states that a central couple of triangles is axial. The converse statement, that an axial couple of triangles is central, is equivalent (either can be used to prove the other). Desargues' theorem can be proved in the real projective plane, and with suitable modifications for special cases, in the Euclidean plane. Projective planes in which central and axial perspectivity of triangles are equivalent are called Desarguesian planes.

There are ten points associated with these two kinds of perspective: six on the two triangles, three on the axis of perspectivity, and one at the center of perspectivity. Dually, there are also ten lines associated with two perspective triangles: three sides of the triangles, three lines through the center of perspectivity, and the axis of perspectivity. These ten points and ten lines form an instance of the Desargues configuration.

If two triangles are a central couple in at least two different ways (with two different associations of corresponding vertices, and two different centers of perspectivity) then they are perspective in three ways. This is one of the equivalent forms of Pappus's (hexagon) theorem.^[5] When this happens, the nine associated points (six triangle vertices and three centers) and nine associated lines (three through each perspective center) form an instance of the Pappus configuration.

The Reye configuration is formed by four quadruply perspective tetrahedra in an analogous way to the Pappus configuration.

Notes

↑ Young 1930 , p. 28
↑ Young 1930 , p. 29
↑ Dembowski 1968 , p. 26
↑ H. S. M. Coxeter (1942) Non-Euclidean Geometry, University of Toronto Press, reissued 1998 by Mathematical Association of America, ISBN 0-88385-522-4 . 21,2.
↑ Coxeter 1969 , p. 233 exercise 2

Related Research Articles

In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts. The basic intuitions are that projective space has more points than Euclidean space, for a given dimension, and that geometric transformations are permitted that transform the extra points to Euclidean points, and vice versa.

In mathematics, affine geometry is what remains of Euclidean geometry when ignoring the metric notions of distance and angle.

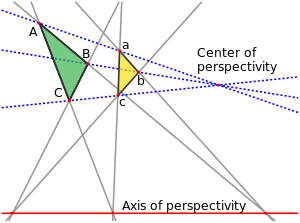
In projective geometry, Desargues's theorem, named after Girard Desargues, states:

In finite geometry, the Fano plane is a finite projective plane with the smallest possible number of points and lines: 7 points and 7 lines, with 3 points on every line and 3 lines through every point. These points and lines cannot exist with this pattern of incidences in Euclidean geometry, but they can be given coordinates using the finite field with two elements. The standard notation for this plane, as a member of a family of projective spaces, is PG(2, 2). Here, PG stands for "projective geometry", the first parameter is the geometric dimension and the second parameter is the order.

In projective geometry, duality or plane duality is a formalization of the striking symmetry of the roles played by points and lines in the definitions and theorems of projective planes. There are two approaches to the subject of duality, one through language and the other a more functional approach through special mappings. These are completely equivalent and either treatment has as its starting point the axiomatic version of the geometries under consideration. In the functional approach there is a map between related geometries that is called a duality. Such a map can be constructed in many ways. The concept of plane duality readily extends to space duality and beyond that to duality in any finite-dimensional projective geometry.

<span class="mw-page-title-main">Pascal's theorem</span> Theorem on the collinearity of three points generated from a hexagon inscribed on a conic

In projective geometry, Pascal's theorem states that if six arbitrary points are chosen on a conic and joined by line segments in any order to form a hexagon, then the three pairs of opposite sides of the hexagon meet at three points which lie on a straight line, called the Pascal line of the hexagon. It is named after Blaise Pascal.

<span class="mw-page-title-main">Incidence structure</span> Abstract mathematical system of two types of objects and a relation between them

In mathematics, an incidence structure is an abstract system consisting of two types of objects and a single relationship between these types of objects. Consider the points and lines of the Euclidean plane as the two types of objects and ignore all the properties of this geometry except for the relation of which points are on which lines for all points and lines. What is left is the incidence structure of the Euclidean plane.

The Sylvester–Gallai theorem in geometry states that every finite set of points in the Euclidean plane has a line that passes through exactly two of the points or a line that passes through all of them. It is named after James Joseph Sylvester, who posed it as a problem in 1893, and Tibor Gallai, who published one of the first proofs of this theorem in 1944.

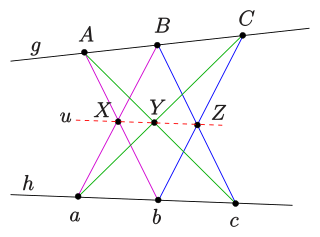
<span class="mw-page-title-main">Pappus's hexagon theorem</span> Geometry theorem

In mathematics, Pappus's hexagon theorem states that

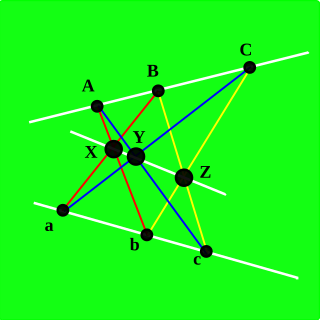
<span class="mw-page-title-main">Pappus configuration</span> Geometric configuration of 9 points and 9 lines

In geometry, the Pappus configuration is a configuration of nine points and nine lines in the Euclidean plane, with three points per line and three lines through each point.

<span class="mw-page-title-main">Complete quadrangle</span> Geometric figure made of 4 points connected by 6 lines

In mathematics, specifically in incidence geometry and especially in projective geometry, a complete quadrangle is a system of geometric objects consisting of any four points in a plane, no three of which are on a common line, and of the six lines connecting the six pairs of points. Dually, a complete quadrilateral is a system of four lines, no three of which pass through the same point, and the six points of intersection of these lines. The complete quadrangle was called a tetrastigm by Lachlan (1893), and the complete quadrilateral was called a tetragram; those terms are occasionally still used.

In geometry, collinearity of a set of points is the property of their lying on a single line. A set of points with this property is said to be collinear. In greater generality, the term has been used for aligned objects, that is, things being "in a line" or "in a row".

Geometry is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. Geometry is one of the oldest mathematical sciences.

<span class="mw-page-title-main">Configuration (geometry)</span> Points and lines with equal incidences

In mathematics, specifically projective geometry, a configuration in the plane consists of a finite set of points, and a finite arrangement of lines, such that each point is incident to the same number of lines and each line is incident to the same number of points.

In geometry, the Desargues configuration is a configuration of ten points and ten lines, with three points per line and three lines per point. It is named after Girard Desargues.

A conic section, conic or a quadratic curve is a curve obtained from a cone's surface intersecting a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though it was sometimes called as a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties.

In geometry and in its applications to drawing, a perspectivity is the formation of an image in a picture plane of a scene viewed from a fixed point.

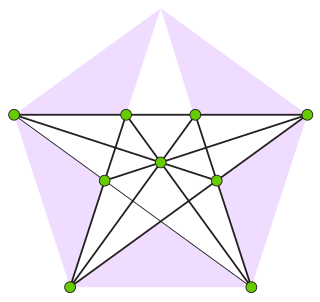
In geometry, the Perles configuration is a system of nine points and nine lines in the Euclidean plane for which every combinatorially equivalent realization has at least one irrational number as one of its coordinates. It can be constructed from the diagonals and symmetry lines of a regular pentagon, and their crossing points. In turn, it can be used to construct higher-dimensional convex polytopes that cannot be given rational coordinates, having the fewest vertices of any known example. All of the realizations of the Perles configuration in the projective plane are equivalent to each other under projective transformations.

In geometry, the Reye configuration, introduced by Theodor Reye (1882), is a configuration of 12 points and 16 lines. Each point of the configuration belongs to four lines, and each line contains three points. Therefore, in the notation of configurations, the Reye configuration is written as $124163$ .

In Euclidean geometry, trilinear polarity is a certain correspondence between the points in the plane of a triangle not lying on the sides of the triangle and lines in the plane of the triangle not passing through the vertices of the triangle. "Although it is called a polarity, it is not really a polarity at all, for poles of concurrent lines are not collinear points." It was Jean-Victor Poncelet (1788–1867), a French engineer and mathematician, who introduced the idea of the trilinear polar of a point in 1865.

References

Coxeter, Harold Scott MacDonald (1969), Introduction to Geometry (2nd ed.), New York: John Wiley & Sons, ISBN 978-0-471-50458-0, MR 0123930
Dembowski, Peter (1968), Finite geometries , Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 44, Berlin, New York: Springer-Verlag, ISBN 3-540-61786-8, MR 0233275
Young, John Wesley (1930), Projective Geometry, The Carus Mathematical Monographs (#4), Mathematical Association of America

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Young 1930 , p. 28

[2] Young 1930 , p. 29

[3] Dembowski 1968 , p. 26

[4] H. S. M. Coxeter (1942) Non-Euclidean Geometry, University of Toronto Press, reissued 1998 by Mathematical Association of America, ISBN 0-88385-522-4 . 21,2.

[5] Coxeter 1969 , p. 233 exercise 2

[1]

[2]

[3]

[4]

[5]