In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or abstract polyhedra, but not all can also be constructed as geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron.

In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts. The basic intuitions are that projective space has more points than Euclidean space, for a given dimension, and that geometric transformations are permitted that transform the extra points to Euclidean points, and vice versa.

In mathematics, affine geometry is what remains of Euclidean geometry when ignoring the metric notions of distance and angle.

In projective geometry, Desargues's theorem, named after Girard Desargues, states:

In finite geometry, the Fano plane is a finite projective plane with the smallest possible number of points and lines: 7 points and 7 lines, with 3 points on every line and 3 lines through every point. These points and lines cannot exist with this pattern of incidences in Euclidean geometry, but they can be given coordinates using the finite field with two elements. The standard notation for this plane, as a member of a family of projective spaces, is PG(2, 2). Here, PG stands for "projective geometry", the first parameter is the geometric dimension and the second parameter is the order.

In mathematics, a regular polytope is a polytope whose symmetry group acts transitively on its flags, thus giving it the highest degree of symmetry. In particular, all its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are themselves regular polytopes of dimension j≤ n.

In geometry, the 16-cell is the regular convex 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol {3,3,4}. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century. It is also called C16, hexadecachoron, or hexdecahedroid [sic?].

In mathematics, an incidence structure is an abstract system consisting of two types of objects and a single relationship between these types of objects. Consider the points and lines of the Euclidean plane as the two types of objects and ignore all the properties of this geometry except for the relation of which points are incident on which lines for all points and lines. What is left is the incidence structure of the Euclidean plane.

In geometry, an arrangement of lines is the subdivision of the plane formed by a collection of lines. Problems of counting the features of arrangements have been studied in discrete geometry, and computational geometers have found algorithms for the efficient construction of arrangements.

In combinatorial mathematics, a Levi graph or incidence graph is a bipartite graph associated with an incidence structure. From a collection of points and lines in an incidence geometry or a projective configuration, we form a graph with one vertex per point, one vertex per line, and an edge for every incidence between a point and a line. They are named for Friedrich Wilhelm Levi, who wrote about them in 1942.

In the mathematical field of graph theory, the Desargues graph is a distance-transitive, cubic graph with 20 vertices and 30 edges. It is named after Girard Desargues, arises from several different combinatorial constructions, has a high level of symmetry, is the only known non-planar cubic partial cube, and has been applied in chemical databases.
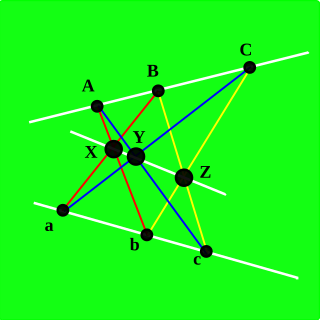
In geometry, the Pappus configuration is a configuration of nine points and nine lines in the Euclidean plane, with three points per line and three lines through each point.

In mathematics, specifically projective geometry, a configuration in the plane consists of a finite set of points, and a finite arrangement of lines, such that each point is incident to the same number of lines and each line is incident to the same number of points.

In the mathematical field of graph theory, the Möbius–Kantor graph is a symmetric bipartite cubic graph with 16 vertices and 24 edges named after August Ferdinand Möbius and Seligmann Kantor. It can be defined as the generalized Petersen graph G(8,3): that is, it is formed by the vertices of an octagon, connected to the vertices of an eight-point star in which each point of the star is connected to the points three steps away from it.

In geometry, the Möbius–Kantor configuration is a configuration consisting of eight points and eight lines, with three points on each line and three lines through each point. It is not possible to draw points and lines having this pattern of incidences in the Euclidean plane, but it is possible in the complex projective plane.

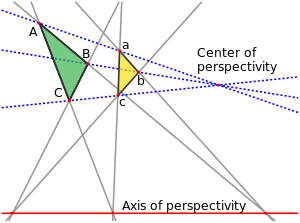
Two figures in a plane are perspective from a pointO, called the center of perspectivity, if the lines joining corresponding points of the figures all meet at O. Dually, the figures are said to be perspective from a line if the points of intersection of corresponding lines all lie on one line. The proper setting for this concept is in projective geometry where there will be no special cases due to parallel lines since all lines meet. Although stated here for figures in a plane, the concept is easily extended to higher dimensions.

In geometry, the Reye configuration, introduced by Theodor Reye (1882), is a configuration of 12 points and 16 lines. Each point of the configuration belongs to four lines, and each line contains three points. Therefore, in the notation of configurations, the Reye configuration is written as 124163.

In mathematics, the Cremona–Richmond configuration is a configuration of 15 lines and 15 points, having 3 points on each line and 3 lines through each point, and containing no triangles. It was studied by Cremona and Richmond. It is a generalized quadrangle with parameters (2,2). Its Levi graph is the Tutte–Coxeter graph.

In geometry, the Grünbaum–Rigby configuration is a symmetric configuration consisting of 21 points and 21 lines, with four points on each line and four lines through each point. Originally studied by Felix Klein in the complex projective plane in connection with the Klein quartic, it was first realized in the Euclidean plane by Branko Grünbaum and John F. Rigby.
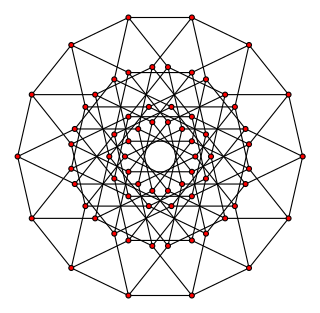
In mathematics, Danzer's configuration is a self-dual configuration of 35 lines and 35 points, having 4 points on each line and 4 lines through each point. It is named after the German geometer Ludwig Danzer and was popularised by Branko Grünbaum. The Levi graph of the configuration is the Kronecker cover of the odd graph O4, and is isomorphic to the middle layer graph of the seven-dimensional hypercube graph Q7. The middle layer graph of an odd-dimensional hypercube graph Q2n+1(n,n+1) is a subgraph whose vertex set consists of all binary strings of length 2n + 1 that have exactly n or n + 1 entries equal to 1, with an edge between any two vertices for which the corresponding binary strings differ in exactly one bit. Every middle layer graph is Hamiltonian.