Related Research Articles

The Archimedean solids are a set of thirteen convex polyhedra whose faces are regular polygons, but not all alike, and whose vertices are all symmetric to each other. The solids were named after Archimedes, although he did not claim credit for them. They belong to the class of uniform polyhedra, the polyhedra with regular faces and symmetric vertices. Some Archimedean solids were portrayed in the works of artists and mathematicians during the Renaissance.

In geometry, a polyhedron is a three-dimensional figure with flat polygonal faces, straight edges and sharp corners or vertices.

In geometry, a star polygon is a type of non-convex polygon. Regular star polygons have been studied in depth; while star polygons in general appear not to have been formally defined, certain notable ones can arise through truncation operations on regular simple or star polygons.
In geometry, a polytope or a tiling is isogonal or vertex-transitive if all its vertices are equivalent under the symmetries of the figure. This implies that each vertex is surrounded by the same kinds of face in the same or reverse order, and with the same angles between corresponding faces.

Norman Woodason Johnson was a mathematician at Wheaton College, Norton, Massachusetts.

In geometry, an arrangement of lines is the subdivision of the Euclidean plane formed by a finite set of lines. An arrangement consists of bounded and unbounded convex polygons, the cells of the arrangement, line segments and rays, the edges of the arrangement, and points where two or more lines cross, the vertices of the arrangement. When considered in the projective plane rather than in the Euclidean plane, every two lines cross, and an arrangement is the projective dual to a finite set of points. Arrangements of lines have also been considered in the hyperbolic plane, and generalized to pseudolines, curves that have similar topological properties to lines. The initial study of arrangements has been attributed to an 1826 paper by Jakob Steiner.

In combinatorial mathematics, a Levi graph or incidence graph is a bipartite graph associated with an incidence structure. From a collection of points and lines in an incidence geometry or a projective configuration, we form a graph with one vertex per point, one vertex per line, and an edge for every incidence between a point and a line. They are named for Friedrich Wilhelm Levi, who wrote about them in 1942.

Branko Grünbaum was a Croatian-born mathematician of Jewish descent and a professor emeritus at the University of Washington in Seattle. He received his Ph.D. in 1957 from Hebrew University of Jerusalem in Israel.
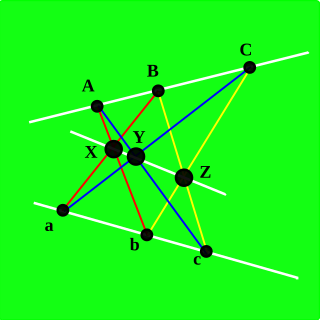
In geometry, the Pappus configuration is a configuration of nine points and nine lines in the Euclidean plane, with three points per line and three lines through each point.

In mathematics, specifically projective geometry, a configuration in the plane consists of a finite set of points, and a finite arrangement of lines, such that each point is incident to the same number of lines and each line is incident to the same number of points.

In geometry, the Desargues configuration is a configuration of ten points and ten lines, with three points per line and three lines per point. It is named after Girard Desargues.
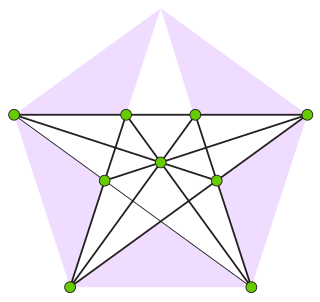
In geometry, the Perles configuration is a system of nine points and nine lines in the Euclidean plane for which every combinatorially equivalent realization has at least one irrational number as one of its coordinates. It can be constructed from the diagonals and symmetry lines of a regular pentagon, and their crossing points. In turn, it can be used to construct higher-dimensional convex polytopes that cannot be given rational coordinates, having the fewest vertices of any known example. All of the realizations of the Perles configuration in the projective plane are equivalent to each other under projective transformations.
Micha Asher Perles is an Israeli mathematician working in geometry, a professor emeritus at the Hebrew University. He earned his Ph.D. in 1964 from the Hebrew University, under the supervision of Branko Grünbaum. His contributions include:

In geometry, the Reye configuration, introduced by Theodor Reye (1882), is a configuration of 12 points and 16 lines. Each point of the configuration belongs to four lines, and each line contains three points. Therefore, in the notation of configurations, the Reye configuration is written as 124163.

In mathematics, the Cremona–Richmond configuration is a configuration of 15 lines and 15 points, having 3 points on each line and 3 lines through each point, and containing no triangles. It was studied by Cremona and Richmond. It is a generalized quadrangle with parameters (2,2). Its Levi graph is the Tutte–Coxeter graph.

In geometry, the Grünbaum–Rigby configuration is a symmetric configuration consisting of 21 points and 21 lines, with four points on each line and four lines through each point. Originally studied by Felix Klein in the complex projective plane in connection with the Klein quartic, it was first realized in the Euclidean plane by Branko Grünbaum and John F. Rigby.
John Frankland Rigby was an English mathematician and academic of the University College of South Wales, Cardiff, when it was part of the University of Wales, and of its successor Cardiff University.

In geometry, the Miquel configuration is a configuration of eight points and six circles in the Euclidean plane, with four points per circle and three circles through each point. Its Levi graph is the Rhombic dodecahedral graph, the skeleton of both Rhombic dodecahedron and Bilinski dodecahedron. The configuration is related to Miquel's theorem.
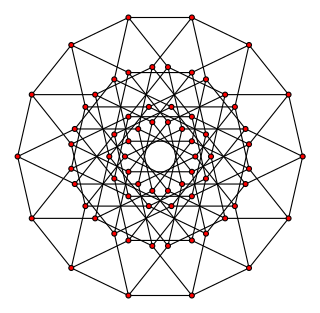
In mathematics, Danzer's configuration is a self-dual configuration of 35 lines and 35 points, having 4 points on each line and 4 lines through each point. It is named after the German geometer Ludwig Danzer and was popularised by Branko Grünbaum. The Levi graph of the configuration is the Kronecker cover of the odd graph O4, and is isomorphic to the middle layer graph of the seven-dimensional hypercube graph Q7. The middle layer graph of an odd-dimensional hypercube graph Q2n+1(n,n+1) is a subgraph whose vertex set consists of all binary strings of length 2n + 1 that have exactly n or n + 1 entries equal to 1, with an edge between any two vertices for which the corresponding binary strings differ in exactly one bit. Every middle layer graph is Hamiltonian.

Roberts's triangle theorem, a result in discrete geometry, states that every simple arrangement of lines has at least triangular faces. Thus, three lines form a triangle, four lines form at least two triangles, five lines form at least three triangles, etc. It is named after Samuel Roberts, a British mathematician who published it in 1889.
References
- ↑ Interim Dean, College of Natural Science & Mathematics – Leah Berman, University of Alaska Fairbanks, July 17, 2018, retrieved 2019-08-17
- ↑ Grünbaum, Branko (2009), Configurations of points and lines, Graduate Studies in Mathematics, vol. 103, American Mathematical Society, Providence, RI, pp. 351–352, doi:10.1090/gsm/103, ISBN 978-0-8218-4308-6, MR 2510707
- ↑ "Two mathematics professors team up", Positively Charged: News from the College of Natural Science & Mathematics, University of Alaska Fairbanks, p. 5, July 17, 2018, retrieved 2019-08-19
- 1 2 3 4 Associate Partners: Leah Wrenn Berman, GReGAS, EuroGIGA Collaborative Research Project, retrieved 2019-08-17
- ↑ Harry J. Berman, Ph.D., Interim Chancellor (PDF), University of Illinois at Springfield , retrieved 2019-08-19
- ↑ Banas, Casey (May 10, 1993), "Quincy High School Wins Scholastic Bowl", Chicago Tribune
- ↑ Pamplin Society of Fellows, Lewis & Clark College, retrieved 2019-08-19
- ↑ Leah Berman at the Mathematics Genealogy Project
- ↑ Williams, Gordon (2018), "Branko Grünbaum, Geometer", Ars Mathematica Contemporanea, 15 (1)
- ↑ McGroarty, Erin (October 2, 2018), "Three women fill open seats on Fairbanks North Star Borough Assembly", Fairbanks Daily News-Miner
- ↑ "Assembly votes for gender-neutral pronouns in ordinance code", Toronto Star, Associated Press, March 2, 2019