This article may be confusing or unclear to readers.(May 2019) |
In geometry and in its applications to drawing, a perspectivity is the formation of an image in a picture plane of a scene viewed from a fixed point.
This article may be confusing or unclear to readers.(May 2019) |
In geometry and in its applications to drawing, a perspectivity is the formation of an image in a picture plane of a scene viewed from a fixed point.
The science of graphical perspective uses perspectivities to make realistic images in proper proportion. According to Kirsti Andersen, the first author to describe perspectivity was Leon Alberti in his De Pictura (1435). [1] In English, Brook Taylor presented his Linear Perspective in 1715, where he explained "Perspective is the Art of drawing on a Plane the Appearances of any Figures, by the Rules of Geometry". [2] In a second book, New Principles of Linear Perspective (1719), Taylor wrote
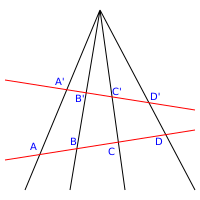
In projective geometry the points of a line are called a projective range, and the set of lines in a plane on a point is called a pencil.
Given two lines and in a projective plane and a point P of that plane on neither line, the bijective mapping between the points of the range of and the range of determined by the lines of the pencil on P is called a perspectivity (or more precisely, a central perspectivity with center P). [4] A special symbol has been used to show that points X and Y are related by a perspectivity; In this notation, to show that the center of perspectivity is P, write
The existence of a perspectivity means that corresponding points are in perspective. The dual concept, axial perspectivity, is the correspondence between the lines of two pencils determined by a projective range.
The composition of two perspectivities is, in general, not a perspectivity. A perspectivity or a composition of two or more perspectivities is called a projectivity (projective transformation, projective collineation and homography are synonyms).
There are several results concerning projectivities and perspectivities which hold in any pappian projective plane: [5]
Theorem: Any projectivity between two distinct projective ranges can be written as the composition of no more than two perspectivities.
Theorem: Any projectivity from a projective range to itself can be written as the composition of three perspectivities.
Theorem: A projectivity between two distinct projective ranges which fixes a point is a perspectivity.
The bijective correspondence between points on two lines in a plane determined by a point of that plane not on either line has higher-dimensional analogues which will also be called perspectivities.
Let Sm and Tm be two distinct m-dimensional projective spaces contained in an n-dimensional projective space Rn. Let Pn−m−1 be an (n − m − 1)-dimensional subspace of Rn with no points in common with either Sm or Tm. For each point X of Sm, the space L spanned by X and Pn-m-1 meets Tm in a point Y = fP(X). This correspondence fP is also called a perspectivity. [6] The central perspectivity described above is the case with n = 2 and m = 1.
Let S2 and T2 be two distinct projective planes in a projective 3-space R3. With O and O* being points of R3 in neither plane, use the construction of the last section to project S2 onto T2 by the perspectivity with center O followed by the projection of T2 back onto S2 with the perspectivity with center O*. This composition is a bijective map of the points of S2 onto itself which preserves collinear points and is called a perspective collineation (central collineation in more modern terminology). [7] Let φ be a perspective collineation of S2. Each point of the line of intersection of S2 and T2 will be fixed by φ and this line is called the axis of φ. Let point P be the intersection of line OO* with the plane S2. P is also fixed by φ and every line of S2 that passes through P is stabilized by φ (fixed, but not necessarily pointwise fixed). P is called the center of φ. The restriction of φ to any line of S2 not passing through P is the central perspectivity in S2 with center P between that line and the line which is its image under φ.


In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect at a single point, but there are some pairs of lines that do not intersect. A projective plane can be thought of as an ordinary plane equipped with additional "points at infinity" where parallel lines intersect. Thus any two distinct lines in a projective plane intersect at exactly one point.

A sphere is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. Formally, a sphere is the set of points that are all at the same distance r from a given point in three-dimensional space. That given point is the center of the sphere, and r is the sphere's radius. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians.

In mathematics, a stereographic projection is a perspective projection of the sphere, through a specific point on the sphere, onto a plane perpendicular to the diameter through the point. It is a smooth, bijective function from the entire sphere except the center of projection to the entire plane. It maps circles on the sphere to circles or lines on the plane, and is conformal, meaning that it preserves angles at which curves meet and thus locally approximately preserves shapes. It is neither isometric nor equiareal.
Elliptic geometry is an example of a geometry in which Euclid's parallel postulate does not hold. Instead, as in spherical geometry, there are no parallel lines since any two lines must intersect. However, unlike in spherical geometry, two lines are usually assumed to intersect at a single point. Because of this, the elliptic geometry described in this article is sometimes referred to as single elliptic geometry whereas spherical geometry is sometimes referred to as double elliptic geometry.

In mathematics, the concept of a projective space originated from the visual effect of perspective, where parallel lines seem to meet at infinity. A projective space may thus be viewed as the extension of a Euclidean space, or, more generally, an affine space with points at infinity, in such a way that there is one point at infinity of each direction of parallel lines.

In mathematics, homogeneous coordinates or projective coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcul, are a system of coordinates used in projective geometry, just as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points, including points at infinity, can be represented using finite coordinates. Formulas involving homogeneous coordinates are often simpler and more symmetric than their Cartesian counterparts. Homogeneous coordinates have a range of applications, including computer graphics and 3D computer vision, where they allow affine transformations and, in general, projective transformations to be easily represented by a matrix. They are also used in fundamental elliptic curve cryptography algorithms.

A 3D projection is a design technique used to display a three-dimensional (3D) object on a two-dimensional (2D) surface. These projections rely on visual perspective and aspect analysis to project a complex object for viewing capability on a simpler plane.

In finite geometry, the Fano plane is a finite projective plane with the smallest possible number of points and lines: 7 points and 7 lines, with 3 points on every line and 3 lines through every point. These points and lines cannot exist with this pattern of incidences in Euclidean geometry, but they can be given coordinates using the finite field with two elements. The standard notation for this plane, as a member of a family of projective spaces, is PG(2, 2). Here PG stands for "projective geometry", the first parameter is the geometric dimension and the second parameter is the order.

A vanishing point is a point on the image plane of a perspective rendering where the two-dimensional perspective projections of mutually parallel lines in three-dimensional space appear to converge. When the set of parallel lines is perpendicular to a picture plane, the construction is known as one-point perspective, and their vanishing point corresponds to the oculus, or "eye point", from which the image should be viewed for correct perspective geometry. Traditional linear drawings use objects with one to three sets of parallels, defining one to three vanishing points.
In projective geometry, duality or plane duality is a formalization of the striking symmetry of the roles played by points and lines in the definitions and theorems of projective planes. There are two approaches to the subject of duality, one through language and the other a more functional approach through special mappings. These are completely equivalent and either treatment has as its starting point the axiomatic version of the geometries under consideration. In the functional approach there is a map between related geometries that is called a duality. Such a map can be constructed in many ways. The concept of plane duality readily extends to space duality and beyond that to duality in any finite-dimensional projective geometry.

In painting, photography, graphical perspective and descriptive geometry, a picture plane is an image plane located between the "eye point" and the object being viewed and is usually coextensive to the material surface of the work. It is ordinarily a vertical plane perpendicular to the sightline to the object of interest.

In geometry, a straight line, usually abbreviated line, is an infinitely long object with no width, depth, or curvature, an idealization of such physical objects as a straightedge, a taut string, or a ray of light. Lines are spaces of dimension one, which may be embedded in spaces of dimension two, three, or higher. The word line may also refer, in everyday life, to a line segment, which is a part of a line delimited by two points.

In geometry, Brianchon's theorem is a theorem stating that when a hexagon is circumscribed around a conic section, its principal diagonals meet in a single point. It is named after Charles Julien Brianchon (1783–1864).
In projective geometry, a homography is an isomorphism of projective spaces, induced by an isomorphism of the vector spaces from which the projective spaces derive. It is a bijection that maps lines to lines, and thus a collineation. In general, some collineations are not homographies, but the fundamental theorem of projective geometry asserts that is not so in the case of real projective spaces of dimension at least two. Synonyms include projectivity, projective transformation, and projective collineation.
In geometry, collinearity of a set of points is the property of their lying on a single line. A set of points with this property is said to be collinear. In greater generality, the term has been used for aligned objects, that is, things being "in a line" or "in a row".

The Lambert azimuthal equal-area projection is a particular mapping from a sphere to a disk. It accurately represents area in all regions of the sphere, but it does not accurately represent angles. It is named for the Swiss mathematician Johann Heinrich Lambert, who announced it in 1772. "Zenithal" being synonymous with "azimuthal", the projection is also known as the Lambert zenithal equal-area projection.
In projective geometry, a collineation is a one-to-one and onto map from one projective space to another, or from a projective space to itself, such that the images of collinear points are themselves collinear. A collineation is thus an isomorphism between projective spaces, or an automorphism from a projective space to itself. Some authors restrict the definition of collineation to the case where it is an automorphism. The set of all collineations of a space to itself form a group, called the collineation group.

In mathematics, a Euclidean plane is a Euclidean space of dimension two, denoted E2. It is a geometric space in which two real numbers are required to determine the position of each point. It is an affine space, which includes in particular the concept of parallel lines. It has also metrical properties induced by a distance, which allows to define circles, and angle measurement.
In mathematics, the classical Möbius plane is the Euclidean plane supplemented by a single point at infinity. It is also called the inversive plane because it is closed under inversion with respect to any generalized circle, and thus a natural setting for planar inversive geometry.

The Steiner conic or more precisely Steiner's generation of a conic, named after the Swiss mathematician Jakob Steiner, is an alternative method to define a non-degenerate projective conic section in a projective plane over a field.