
Euclid was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the Elements treatise, which established the foundations of geometry that largely dominated the field until the early 19th century. His system, now referred to as Euclidean geometry, involved new innovations in combination with a synthesis of theories from earlier Greek mathematicians, including Eudoxus of Cnidus, Hippocrates of Chios, Thales and Theaetetus. With Archimedes and Apollonius of Perga, Euclid is generally considered among the greatest mathematicians of antiquity, and one of the most influential in the history of mathematics.

In mathematics, the four color theorem, or the four color map theorem, states that no more than four colors are required to color the regions of any map so that no two adjacent regions have the same color. Adjacent means that two regions share a common boundary curve segment, not merely a corner where three or more regions meet. It was the first major theorem to be proved using a computer. Initially, this proof was not accepted by all mathematicians because the computer-assisted proof was infeasible for a human to check by hand. The proof has gained wide acceptance since then, although some doubters remain.
James is a common English language surname and given name:

In projective geometry, Desargues's theorem, named after Girard Desargues, states:
Moebius, Mœbius, Möbius or Mobius may refer to:
Pappus's theorem may refer to:

Pappus of Alexandria was one of the last great Greek mathematicians of antiquity; he is known for his Synagoge (Συναγωγή) or Collection, and for Pappus's hexagon theorem in projective geometry. Nothing is known of his life, other than what can be found in his own writings: that he had a son named Hermodorus, and was a teacher in Alexandria.

In combinatorial mathematics, a Levi graph or incidence graph is a bipartite graph associated with an incidence structure. From a collection of points and lines in an incidence geometry or a projective configuration, we form a graph with one vertex per point, one vertex per line, and an edge for every incidence between a point and a line. They are named for Friedrich Wilhelm Levi, who wrote about them in 1942.
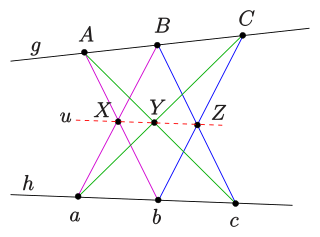
In mathematics, Pappus's hexagon theorem states that

In the mathematical field of graph theory, the Desargues graph is a distance-transitive, cubic graph with 20 vertices and 30 edges. It is named after Girard Desargues, arises from several different combinatorial constructions, has a high level of symmetry, is the only known non-planar cubic partial cube, and has been applied in chemical databases.
Continuity or continuous may refer to:
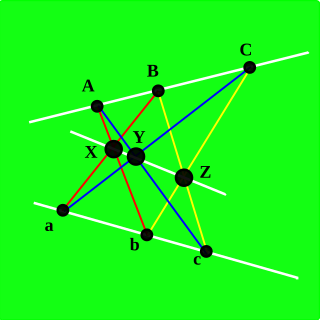
In geometry, the Pappus configuration is a configuration of nine points and nine lines in the Euclidean plane, with three points per line and three lines through each point.

In mathematics, specifically projective geometry, a configuration in the plane consists of a finite set of points, and a finite arrangement of lines, such that each point is incident to the same number of lines and each line is incident to the same number of points.

In the mathematical field of graph theory, the Pappus graph is a bipartite, 3-regular, undirected graph with 18 vertices and 27 edges, formed as the Levi graph of the Pappus configuration. It is named after Pappus of Alexandria, an ancient Greek mathematician who is believed to have discovered the "hexagon theorem" describing the Pappus configuration. All the cubic, distance-regular graphs are known; the Pappus graph is one of the 13 such graphs.
De Bruijn is a Dutch surname meaning "the brown". Notable people with the surname include:

In geometry, the Möbius configuration or Möbius tetrads is a certain configuration in Euclidean space or projective space, consisting of two mutually inscribed tetrahedra: each vertex of one tetrahedron lies on a face plane of the other tetrahedron and vice versa. Thus, for the resulting system of eight points and eight planes, each point lies on four planes, and each plane contains four points.
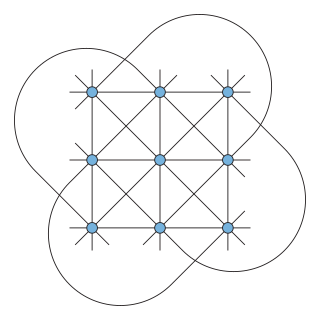
In geometry, the Hesse configuration is a configuration of 9 points and 12 lines with three points per line and four lines through each point. It can be realized in the complex projective plane as the set of inflection points of an elliptic curve, but it has no realization in the Euclidean plane. It was introduced by Colin Maclaurin and studied by Hesse (1844), and is also known as Young's geometry, named after the later work of John Wesley Young on finite geometry.
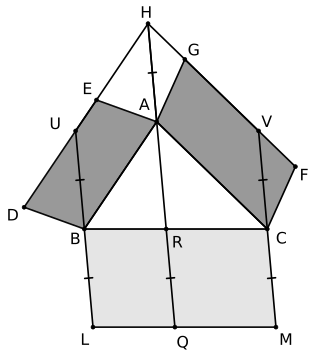
Pappus's area theorem describes the relationship between the areas of three parallelograms attached to three sides of an arbitrary triangle. The theorem, which can also be thought of as a generalization of the Pythagorean theorem, is named after the Greek mathematician Pappus of Alexandria, who discovered it.
This page is based on this
Wikipedia article Text is available under the
CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.












