Projective range

Last updated October 23, 2019

In mathematics, a projective range is a set of points in projective geometry considered in a unified fashion. A projective range may be a projective line or a conic. A projective range is the dual of a pencil of lines on a given point. For instance, a correlation interchanges the points of a projective range with the lines of a pencil. A projectivity is said to act from one range to another, though the two ranges may coincide as sets.

Mathematics Field of study concerning quantity, patterns and change

Mathematics includes the study of such topics as quantity, structure (algebra), space (geometry), and change. It has no generally accepted definition.

Projective geometry is a topic in mathematics. It is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts. The basic intuitions are that projective space has more points than Euclidean space, for a given dimension, and that geometric transformations are permitted that transform the extra points to Euclidean points, and vice versa.

In geometry, a real projective line is an extension of the usual concept of line that has been historically introduced to solve a problem set by visual perspective: two parallel lines do not intersect but seem to intersect "at infinity". For solving this problem, points at infinity have been introduced, in such a way that in a real projective plane, two distinct projective lines meet in exactly one point. The set of these points at infinity, the "horizon" of the visual perspective in the plane, is a real projective line. It is the circle of directions emanating from an observer situated at any point, with opposite points identified. A model of the real projective line is the projectively extended real line. Drawing a line to represent the horizon in visual perspective, an additional point at infinity is added to represent the collection of lines parallel to the horizon.

A projective range expresses projective invariance of the relation of projective harmonic conjugates. Indeed, three points on a projective line determine a fourth by this relation. Application of a projectivity to this quadruple results in four points likewise in the harmonic relation. Such a quadruple of points is termed a harmonic range. In 1940 Julian Coolidge described this structure and identified its originator:^[1]

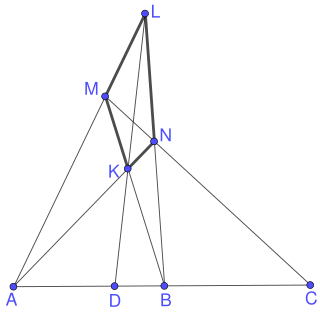
In projective geometry, the harmonic conjugate point of an ordered triple of points on the real projective line is defined by the following construction:

Julian Lowell Coolidge was an American mathematician, historian and a professor and chairman of the Harvard University Mathematics Department.

Two fundamental one-dimensional forms such as point ranges, pencils of lines, or of planes are defined as projective, when their members are in one-to-one correspondence, and a harmonic set of one ... corresponds to a harmonic set of the other. ... If two one-dimensional forms are connected by a train of projections and intersections, harmonic elements will correspond to harmonic elements, and they are projective in the sense of Von Staudt.

Conic ranges

When a conic is chosen for a projective range, and a particular point E on the conic is selected as origin, then addition of points may be defined as follows:^[2]

Let A and B be in the range (conic) and AB the line connecting them. Let L be the line through E and parallel to AB. The "sum of points A and B", A + B, is the intersection of L with the range.^{[ citation needed ]}

The circle and hyperbola are instances of a conic and the summation of angles on either can be generated by the method of "sum of points", provided points are associated with angles on the circle and hyperbolic angles on the hyperbola.

Circle simple curve of Euclidean geometry

A circle is a shape consisting of all points in a plane that are a given distance from a given point, the centre; equivalently it is the curve traced out by a point that moves in a plane so that its distance from a given point is constant. The distance between any point of the circle and the centre is called the radius. This article is about circles in Euclidean geometry, and, in particular, the Euclidean plane, except where otherwise noted.

In mathematics, a hyperbola is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows. The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane and a double cone. If the plane intersects both halves of the double cone but does not pass through the apex of the cones, then the conic is a hyperbola.

In plane geometry, an angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle. Angles formed by two rays lie in a plane, but this plane does not have to be a Euclidean plane. Angles are also formed by the intersection of two planes in Euclidean and other spaces. These are called dihedral angles. Angles formed by the intersection of two curves in a plane are defined as the angle determined by the tangent rays at the point of intersection. Similar statements hold in space, for example, the spherical angle formed by two great circles on a sphere is the dihedral angle between the planes determined by the great circles.

Related Research Articles

In classical mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.

Perpendicular Relationship between two lines that meet at a right angle (90 degrees)

In elementary geometry, the property of being perpendicular (perpendicularity) is the relationship between two lines which meet at a right angle. The property extends to other related geometric objects.

Elliptic geometry is an example of a geometry in which Euclid's parallel postulate does not hold. Instead, as in spherical geometry, there are no parallel lines since any two lines must intersect. However, unlike in spherical geometry, two lines are usually assumed to intersect at a single point. Because of this, the elliptic geometry described in this article is sometimes referred to as single elliptic geometry whereas spherical geometry is sometimes referred to as double elliptic geometry.

In algebraic geometry and computational geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the general case situation, as opposed to some more special or coincidental cases that are possible, which is referred to as special position. Its precise meaning differs in different settings.

In geometry, a degenerate conic is a conic that fails to be an irreducible curve. This means that the defining equation is factorable over the complex numbers as the product of two linear polynomials.

In geometry, a locus is a set of all points, whose location satisfies or is determined by one or more specified conditions.

In mathematics, a cubic plane curve is a plane algebraic curve C defined by a cubic equation

In projective geometry, Pascal's theorem states that if six arbitrary points are chosen on a conic and joined by line segments in any order to form a hexagon, then the three pairs of opposite sides of the hexagon meet at three points which lie on a straight line, called the Pascal line of the hexagon. It is named after Blaise Pascal.

Focus (geometry) fixed reference point; special points with reference to which any of a variety of curves is constructed

In geometry, focuses or foci, singular focus, are special points with reference to which any of a variety of curves is constructed. For example, one or two foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola. In addition, two foci are used to define the Cassini oval and the Cartesian oval, and more than two foci are used in defining an n-ellipse.

In mathematics, a hyperbolic angle is a geometric figure that defines a hyperbolic sector. The relationship of a hyperbolic angle to a hyperbola parallels the relationship of an "ordinary" angle to a circle.

Complete quadrangle four points that determine six distinct lines

In mathematics, specifically in incidence geometry and especially in projective geometry, a complete quadrangle is a system of geometric objects consisting of any four points in a plane, no three of which are on a common line, and of the six lines connecting the six pairs of points. Dually, a complete quadrilateral is a system of four lines, no three of which pass through the same point, and the six points of intersection of these lines. The complete quadrangle was called a tetrastigm by Lachlan (1893), and the complete quadrilateral was called a tetragram; those terms are occasionally still used.

In mathematics, the Cayley–Bacharach theorem is a statement about cubic curves in the projective plane $P 2$ . The original form states:

Apollonian circles are two families of circles such that every circle in the first family intersects every circle in the second family orthogonally, and vice versa. These circles form the basis for bipolar coordinates. They were discovered by Apollonius of Perga, a renowned Greek geometer.

In mathematics, a Benz plane is a type of 2-dimensional geometrical structure, named after the German mathematician Walter Benz. The term was applied to a group of objects that arise from a common axiomatization of certain structures and split into three families, which were introduced separately: Möbius planes, Laguerre planes, and Minkowski planes.

In mathematics, a conic section is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties.

In geometry, the unit hyperbola is the set of points (x,y) in the Cartesian plane that satisfy the implicit equation $In the study of indefinite orthogonal groups, the unit hyperbola forms the basis for an alternative radial length$

In Euclidean and projective geometry, just as two (distinct) points determine a line, five points determine a conic. There are additional subtleties for conics that do not exist for lines, and thus the statement and its proof for conics are both more technical than for lines.

The terminology of algebraic geometry changed drastically during the twentieth century, with the introduction of the general methods, initiated by David Hilbert and the Italian school of algebraic geometry in the beginning of the century, and later formalized by André Weil, Jean-Pierre Serre and Alexander Grothendieck. Much of the classical terminology, mainly based on case study, was simply abandoned, with the result that books and papers written before this time can be hard to read. This article lists some of this classical terminology, and describes some of the changes in conventions.

References

↑ J. L. Coolidge (1940) A History of Geometrical Methods, page 98, Oxford University Press (Dover Publications 2003)
↑ Viktor Prasolov & Yuri Solovyev (1997) Elliptic Functions and Elliptic Integrals, page one, Translations of Mathematical Monographs volume 170, American Mathematical Society

H. S. M. Coxeter (1955) The Real Projective Plane, University of Toronto Press, p 20 for line, p 101 for conic.

The University of Toronto Press is a Canadian scholarly publisher and book distributor founded in 1901.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] J. L. Coolidge (1940) A History of Geometrical Methods, page 98, Oxford University Press (Dover Publications 2003)

[2] Viktor Prasolov & Yuri Solovyev (1997) Elliptic Functions and Elliptic Integrals, page one, Translations of Mathematical Monographs volume 170, American Mathematical Society